
- •14.1. Определение кратного интеграла.
- •14.2. Двойные интегралы
- •14.2.1. Области на плоскости
- •14.2.2. Повторный интеграл
- •14.2.4. Замена переменных в двойном интеграле
- •14.3. Тройные интегралы
- •14.3.1. Области в пространстве
- •3.2. Вычисление тройного интеграла
- •14.3.3. Замена переменных в тройном интеграле
- •Переход в тройном интеграле к цилиндрическим координатам
- •14.5. Криволинейные интегралы
- •14.5.1. Криволинейные интегралы первого рода (ки-1)
- •Вычисление ки-1
- •Некоторые приложения ки-1
- •14.5.2. Криволинейные интегралы второго рода (ки-2)
- •Вычисление ки-2
- •Следствия. А) Для плоской линии ab: и функций , :
- •Независимость ки-2 от пути интегрирования
- •Связь между ки-1 и ки-2
- •Связь ки-2 с двойным интегралом (формула Грина)
- •14.6. Поверхностные интегралы
- •14.6.1. Двусторонние поверхности и их ориентация
- •14.6.2. Поверхностный интеграл первого рода (пи-1)
- •Вычисление пи-1
- •Некоторые приложения пи-1
- •Задания. 1. Записать линейные свойства пи-1.
- •14.6.3. Поверхностные интегралы второго рода (пи-2)
- •Вычисление пи-2
- •Связь между пи-1 и пи-2
14.3.3. Замена переменных в тройном интеграле
Пусть
функции
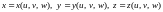 осу-ществляют взаимно однозначное
непрерывно дифференцируемое отображение
области из
пространства Ouvw на
область V пространства
Oxyz. Тогда
существует обратное непрерывно
дифферен-цируемое отображение
осу-ществляют взаимно однозначное
непрерывно дифференцируемое отображение
области из
пространства Ouvw на
область V пространства
Oxyz. Тогда
существует обратное непрерывно
дифферен-цируемое отображение
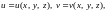
 области V на область
, если якобиан
преобразования
области V на область
, если якобиан
преобразования
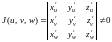
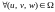 .
.
Величины u, v, w можно рассматривать как прямоугольные координаты для точек области и в то же время как криволинейные координаты точек области V. Точки пространства Oxyz , для которых одна из координат u, v, w сохраняет постоянное значение, образуют координатную поверхность. Всего будет три семейства таких поверхностей.
Теорема 14.5.
Пусть
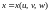 ,
,
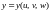 ,
,
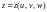 есть дифференцируемое преобразование
области из
пространства Ouvw в
область V из пространства
Oxyz. Тогда
есть дифференцируемое преобразование
области из
пространства Ouvw в
область V из пространства
Oxyz. Тогда
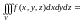
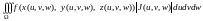 (14.16)
(14.16)
З а м е ч а н и е. Последнее равенство сохраняет справедливость, когда условие взаимно однозначного соответствия между областями V и нарушается в отдельных точках или вдоль отдельных линий, или на отдельных поверхностях.
Переход в тройном интеграле к цилиндрическим координатам
Формулы
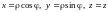 преобразуют цилиндрические координаты
преобразуют цилиндрические координаты
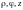 точки M в декартовы
координаты этой точки и переводят
область изменения криволинейных
координат
точки M в декартовы
координаты этой точки и переводят
область изменения криволинейных
координат
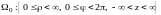 (или
(или
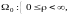
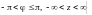 )
на все пространство Oxyz.
Геометрически:
– радиус-вектор OM
точки P – проекции
точки M на плоскость
Oxy;
– угол между Ox и OP;
z – аппликата
точки M (рис. 14.17).
)
на все пространство Oxyz.
Геометрически:
– радиус-вектор OM
точки P – проекции
точки M на плоскость
Oxy;
– угол между Ox и OP;
z – аппликата
точки M (рис. 14.17).
О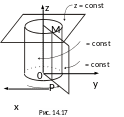 братное
преобразование задается формулами:
братное
преобразование задается формулами:
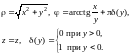
Фиксируя
в последних формулах
,
получим тройку координатных поверхностей:
круговой цилиндр с осью Oz
, полуплоскость, исходящую из оси Oz,
и плоскость, параллельную плоскости
Oxy (рис. 14.17) Якобиан
преобразования
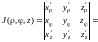
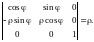
При переходе в тройном интеграле к цилиндрическим координатам формула (14.16) примет вид:
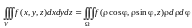
, (14.17)
где – область изменения цилиндрических координат точек области V из Oxyz.
Переход к сферическим координатам
Формулы
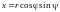 ,
,
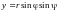 ,
,
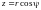 преоб-разуют сферические координаты
преоб-разуют сферические координаты
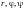 точки M в декартовы
ко-
ординаты этой точки и переводят
область
точки M в декартовы
ко-
ординаты этой точки и переводят
область
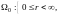
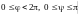 (или
(или
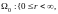
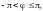
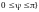 )
изменения сферических координат на
все пространство Oxyz.
)
изменения сферических координат на
все пространство Oxyz.
Г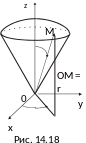 еометрически:
r – радиус-вектор OM
точки M;
– угол между осью Ox
и проекцией радиуса-вектора r
на плоскость Oxy;
– угол между осью Oz
и радиус-вектором r,
отсчитываемый по ходу стрелки часов
(рис. 14.18). Обратное преобразование имеет
вид
еометрически:
r – радиус-вектор OM
точки M;
– угол между осью Ox
и проекцией радиуса-вектора r
на плоскость Oxy;
– угол между осью Oz
и радиус-вектором r,
отсчитываемый по ходу стрелки часов
(рис. 14.18). Обратное преобразование имеет
вид
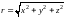 ,
,
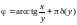 ,
,
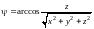 ,
,
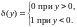
Фиксируя
в последних формулах
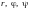 ,
получим тройку координатных поверхностей:
сферу, полуплоскость, полуконус,
соответственно, (рис. 14.18). Якобиан
преобразования
,
получим тройку координатных поверхностей:
сферу, полуплоскость, полуконус,
соответственно, (рис. 14.18). Якобиан
преобразования
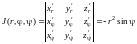 .
.
При переходе в тройном интеграле к сферическим координатам справедлива формула:
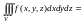

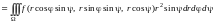 , (14.18)
, (14.18)
где – область изменения сферических координат точек области V из Oxyz.
Пример 12.
Вычислить тройной интеграл
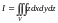 ,
где
,
где
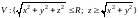 .
.
Область V
ограничена полусферой
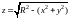 и полуконусом
и полуконусом
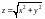 (рис. 14.18). Для удобства вычисления
трой-
ного интеграла перейдем к
сферическим координатам по фор-
мулам:
(рис. 14.18). Для удобства вычисления
трой-
ного интеграла перейдем к
сферическим координатам по фор-
мулам:
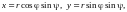 ,
при этом
,
при этом
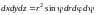 .
Неравенства, описывающие V
, преобра-зуются: а)
.
Неравенства, описывающие V
, преобра-зуются: а)
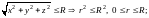
б)
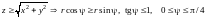 .
.
Т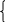 ак
как нет ограничений на
,
то
ак
как нет ограничений на
,
то
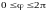 .
В итоге область ин-
.
В итоге область ин-
тегрирования в
сферических координатах есть
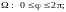
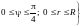 (этот же результат можно было усмотреть
из чертежа). Тогда по формуле (14.18)
(этот же результат можно было усмотреть
из чертежа). Тогда по формуле (14.18)
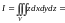
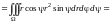
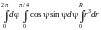 =повторный
интеграл «расщепился» в
произведение определенных интегралов
= =
=повторный
интеграл «расщепился» в
произведение определенных интегралов
= =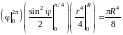 .
.
Пример
13. Вычислить
тройной интеграл
 ,
где V ограничена
полусферой
,
где V ограничена
полусферой
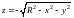 ,
цилиндром
и
плоскостью
,
цилиндром
и
плоскостью
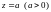 .
.
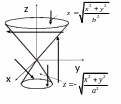
Тело V
и проекция его на плоскость Oxy
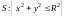 –
круг радиуса R изображены
на рис. 14.19 и 14.20. Для вычисления I
перейдем к цилиндрическим координатам
по формулам
–
круг радиуса R изображены
на рис. 14.19 и 14.20. Для вычисления I
перейдем к цилиндрическим координатам
по формулам
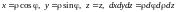 .
Поверхности,
ограничивающие V
, преобразуются: а)
.
Поверхности,
ограничивающие V
, преобразуются: а)
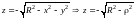 ;
;
б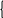 )
)
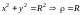 ;
в) z = a
. Так как нет ограничений на ко-
ординату
,
то
;
в) z = a
. Так как нет ограничений на ко-
ординату
,
то
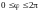 (или
(или
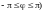 .Область
интегрирова-
ния в цилиндрических
координатах есть
.Область
интегрирова-
ния в цилиндрических
координатах есть
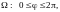

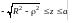 .
.
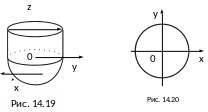
Тогда по формуле (14.17)
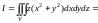
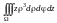 =
=
=
=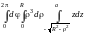 =
=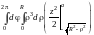 =
=
=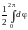
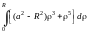 =
=
=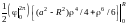 =
=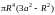 .
.
14.4. Некоторые приложения двойных
и тройных интегралов
1. Площадь фигуры. а) Для плоской фигуры
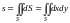 .
(14.19)
.
(14.19)
б) Площадь части искривленной поверхности рассматривается в разделе 14.6 этой главы.
2. Объем тела
V:
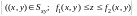 (
(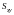 – проекция V на
плоскость Oxy):
– проекция V на
плоскость Oxy):
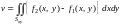 (14.20)
(14.20)
или
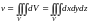 .
(14.21)
.
(14.21)
3. Масса. а)
Если
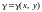 – поверхностная плотность массы плоской
фигуры
,
то
– поверхностная плотность массы плоской
фигуры
,
то
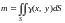 .
(14.22)
.
(14.22)
б) если
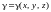 – объемная плотность массы тела
– объемная плотность массы тела
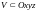 ,
то
,
то
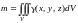 .
(14.23)
.
(14.23)
Для
однородных фигур и тел плотность
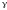 примем равной единице.
примем равной единице.
4. Статические
моменты и координаты центра тяжести.
а) Для плоской фигуры
c плотностью
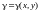 и массой m статические
моменты относительно координатных осей
Oy и Ox
соответственно:
и массой m статические
моменты относительно координатных осей
Oy и Ox
соответственно:
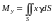 ,
,
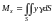 ;
;
координаты центра тяжести:
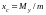 ,
,
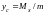 .
.
б) Для
тела V с
плотностью
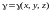 и массой m
статичес-кие моменты относительно
координатных плоскостей Oyz,
Oxz, Oxy:
и массой m
статичес-кие моменты относительно
координатных плоскостей Oyz,
Oxz, Oxy:
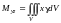 ,
,
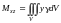 ,
,
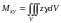 ;
;
координаты центра тяжести:
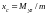 ,
,
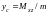 ,
,
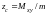 .
.
Пример 14. Найти
массу пластинки
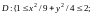
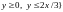 с поверхностной плотностью
с поверхностной плотностью
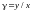 .
.
По формуле
(14.22)
 .
Область D и
подынтегральная функция совпадают с
областью интегрирования и функцией из
примера 9 в разд. 14.2.4 при
.
Область D и
подынтегральная функция совпадают с
областью интегрирования и функцией из
примера 9 в разд. 14.2.4 при
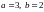 ;
там же вычислен этот двойной интеграл,
поэтому
;
там же вычислен этот двойной интеграл,
поэтому
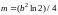 и при
и при
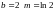 .
.
Пример
15. Найти массу
тела.
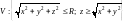 ,
если объемная плотность
,
если объемная плотность
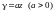 .
.
По формуле
(14.23)
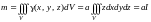 .
Тройной интеграл I по
данной области V
вычислен в примере 12 из разд. 14.3.3,
.
Тройной интеграл I по
данной области V
вычислен в примере 12 из разд. 14.3.3,
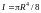 ,
и потому
,
и потому
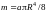 .
.
Пример 16. Найти
объем тела
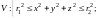
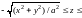
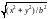 ;
;
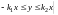 ,
,
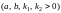 .
.
Из формулы
(14.21)
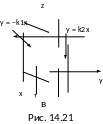
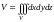 . Тело V ограничено
сферами, полуконусами и плоскостями
(рис. 14.21).
. Тело V ограничено
сферами, полуконусами и плоскостями
(рис. 14.21).
а
z
х2 + у2 + z2 = r22

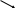
х2 + у2 + z2 = r12



y

x
Из анализа уравнений
и вида поверхностей следует
целесо-
образность перехода к
сферическим координатам
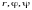 по формулам:
,
,
.
Поверхности, ограничивающие V,
преобразуются:
по формулам:
,
,
.
Поверхности, ограничивающие V,
преобразуются:
1)
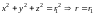 ;
;
2)
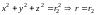 ;
;
3)
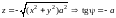 или
или
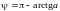 ;
;
4)
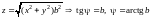 ;
;
5)
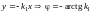 ;
6)
;
6)
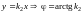 .
.
Область изменения
сферических координат точек области V
есть
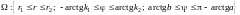 .
.
Тогда
в силу формулы (14.18)
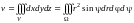 =
=
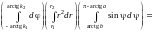
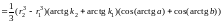 .
.
