14.3. Тройные интегралы

14.3.1. Области в пространстве

Определение. Область 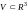назовем правильной в на-правлении Oz (правильной в направлении Ox, правильной в на-правлении Oy), если прямая, проходящая через внутреннюю точку области V параллельно оси Oz (параллельно оси Ox, параллельно оси Oy) пересекает границу области ровно в двух точках.

Область V будет правильной в направлении Oz, если существуют функции и , заданные в S и такие, что координаты точек, принадлежащих V, удовлетворяют условиям: . Тогда символически записывают:

. (14.12)

Если, в свою очередь, область S – правильная в направлении Oy (см. (14.3)), то

. (14.13)

Если область S правильная в направлении Ox (см. (14.4)), то

. (14.14)

Задания. 1. Записать символически правильную в направлении Oy область , если ее проекция на плоскость Oxz, в свою очередь, есть правильная область.

2. Записать символически правильную в направлении Ox область , если ее проекция на плоскость Oyz есть правильная область.

Пример 10. Область V ограничена поверхностями х² + у² = = (z – 2)² и z = 0. Изобразить область и записать как правильную: а) в направлении Оz, б) в направлении Ox.



Рис.14.13

Область V – круговой конус с боковой поверхностью, описываемой уравнением конической поверхности , основанием, лежащим на плоскости z = 0, с вершиной в точке M(0; 0; 2) и осью, совпадающей с Oz (рис. 14.12). Область V – правильная во всех направлениях Ox, Oy, Oz. При z = 0 из уравнения имеем – уравнение окружности радиуса 2; таким образом, в основании конуса круг.

а) Рассмотрим область V как правильную в направлении Oz. Из уравнения имеем . Для точек области V имеем: . Проекция области V на плоскость Oxy есть (рис. 14.13), поэтому в силу (14.12) , где . Так как S – правильная область, то (см. (14.3)) или (см. (14.4)) . Поэтому требуемая запись будет (см. (14.13)) или (см. (14.4)) .

б) Рассматривая область V как правильную в направлении Ox, из уравнения имеем . Линии пересечения плоскости Oyz и конической поверхности находятся из решения системы уравнений: ; в результате имеем – прямые в плоскости Oyz. Итак, проекцией V на плоскость Oyz является область D – треугольник со сторонами z = y + 2, z = –y + 2, z = 0 (рис. 14.14), поэтому в силу (14.12) ,

г де .

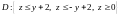Т

2

ак как область D – правильная, то, рассматривая ее как правильную в направлении Oy, имеем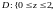 , а потому



3.2. Вычисление тройного интеграла

в декартовых координатах

Пусть правильная в направлении Oz область V ограничена снизу и сверху непересекающимися поверхностями и , а с боков – цилиндрической поверхностью F(x, y) = 0 c образующими, параллельными оси Oz, т.е. , где S – проекция V на плоскости Oxy.

Теорема 14.4. Пусть: 1) в области

задана функция f(x, y,z), интегрируемая по Риману, т.е. существует тройной интеграл ; 2) существует повторный интеграл . Тогда справедлива формула

(14.15)

З а м е ч а н и е. Цилиндрическая поверхность , ограничивающая V, может частично или полностью вырождаться в пространственную линию.

Задания. Записать формулы, связывающие тройной интеграл с повторным, в случаях, когда: 1) область V правильная в на-правлении Ox проецируется на плоскость Oyz; 2) область V правильная в направлении Oy проецируется на плоскость Oxz.

Пример 11. Вычислить , где область V ограничена поверхностями: .

 Поверхности и 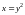есть параболические цилиндры с образующими, параллельными 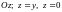– плоскости. Область V – правильная в направлении Oz, а потому для точек, принадлежащих V (рис. 14.15).

Проекция V на плоскость Oxy есть правильная область S, ограниченная линиями и (рис. 14.16), а потому, например (см. (14.3)), и в силу (14.13) . Тогда по формуле (14.15)

= =

= = см. (14.5) =

= =

= = . 