
- •14.1. Определение кратного интеграла.
- •14.2. Двойные интегралы
- •14.2.1. Области на плоскости
- •14.2.2. Повторный интеграл
- •14.2.4. Замена переменных в двойном интеграле
- •14.3. Тройные интегралы
- •14.3.1. Области в пространстве
- •3.2. Вычисление тройного интеграла
- •14.3.3. Замена переменных в тройном интеграле
- •Переход в тройном интеграле к цилиндрическим координатам
- •14.5. Криволинейные интегралы
- •14.5.1. Криволинейные интегралы первого рода (ки-1)
- •Вычисление ки-1
- •Некоторые приложения ки-1
- •14.5.2. Криволинейные интегралы второго рода (ки-2)
- •Вычисление ки-2
- •Следствия. А) Для плоской линии ab: и функций , :
- •Независимость ки-2 от пути интегрирования
- •Связь между ки-1 и ки-2
- •Связь ки-2 с двойным интегралом (формула Грина)
- •14.6. Поверхностные интегралы
- •14.6.1. Двусторонние поверхности и их ориентация
- •14.6.2. Поверхностный интеграл первого рода (пи-1)
- •Вычисление пи-1
- •Некоторые приложения пи-1
- •Задания. 1. Записать линейные свойства пи-1.
- •14.6.3. Поверхностные интегралы второго рода (пи-2)
- •Вычисление пи-2
- •Связь между пи-1 и пи-2
14.2.2. Повторный интеграл
Определение.
Повторный интеграл
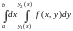 есть приращение первообразной F(x,y)
для
есть приращение первообразной F(x,y)
для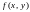 по переменному y,
проинтегрированное по переменному x
, т.е.
по переменному y,
проинтегрированное по переменному x
, т.е.
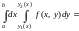
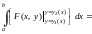
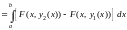 .
.
Определение.
Повторный интеграл
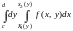 есть приращение первообразной Ф(x,
y) для f
(x, y)
по переменному x,
проинтегрированное по переменному y,
т.е.
есть приращение первообразной Ф(x,
y) для f
(x, y)
по переменному x,
проинтегрированное по переменному y,
т.е.
=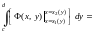
=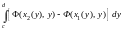 .
.
Пример 3.
Вычислить повторный интеграл
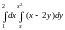 .
.
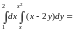 |,
интегрируя внутренний интеграл
по
y, полагаем x
постоянным |
|,
интегрируя внутренний интеграл
по
y, полагаем x
постоянным |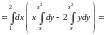
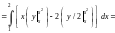
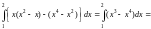
=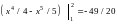 .
.
14.2.3. Вычисление двойного интеграла
в декартовых координатах
Теорема 14.1
Если : 1) функция f(x,y)
интегрируема в правильной в направлении
Oy области S:
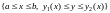 ,
т.е. существует двойной интеграл
,
т.е. существует двойной интеграл
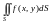 ,
2) существует повторный интеграл
,
то
,
2) существует повторный интеграл
,
то
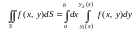
(14.5)
Теорема 14.2.
Если: 1) функция f (x,
y) интегрируема в
правильной в направлении Ox
области
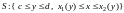 ,
т.е. существует двойной интеграл
, 2) существует повторный интеграл
,
т.е. существует двойной интеграл
, 2) существует повторный интеграл
 ,
то
,
то
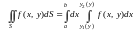
(14.6)
Из приведенных выше теорем следует, что при вычислении повторного интеграла можно изменять порядок интегрирования.
Пример 4.
Изменить порядок интегрирования в
интеграле
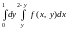 .
.
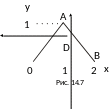 Так как из (14.6)
имеем
Так как из (14.6)
имеем
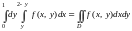 ,
то правильная в направлении Ox
область D ограничена
линиями x = y,
x = 2 – y,
y = 0, y
= 1 (линия y = 1
выродилась в точку) (рис. 14.7). Эта область
является правильной и в направлении
Oy. Так как участок OAB
границы состоит из отрезков прямых
,
то правильная в направлении Ox
область D ограничена
линиями x = y,
x = 2 – y,
y = 0, y
= 1 (линия y = 1
выродилась в точку) (рис. 14.7). Эта область
является правильной и в направлении
Oy. Так как участок OAB
границы состоит из отрезков прямых
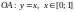 и
и
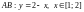 ,
то
,
то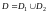 ,
где (см. (14.3))
,
где (см. (14.3))
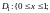
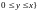 ,
,
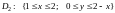 .
.
Итак,
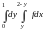 =
=
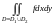 =
=
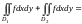
=
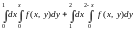 .
.
Пример 5.
Вычислить
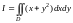 по области D, ограниченной
линиями
по области D, ограниченной
линиями
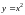 и
и
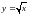 .
.
Изобразим область
D. Для отыскания точек
пересечения парабол
и
решаем уравнение
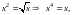
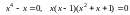 ,
отсюда имеем действительные корни
,
отсюда имеем действительные корни
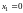 ,
,
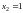 .
Таким образом, параболы пересекаются
в точках
.
Таким образом, параболы пересекаются
в точках
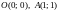 (рис.
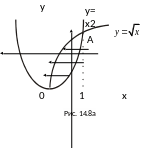
14.8). Рассматривая область D
как правильную в направлении Oy
(рис. 14.8а), имеем (см. (14.3))
(рис.
14.8). Рассматривая область D
как правильную в направлении Oy
(рис. 14.8а), имеем (см. (14.3))
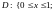
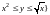 .
По формуле (14.3)
.
По формуле (14.3)
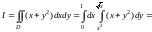
=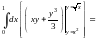
=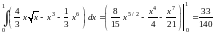 .
.
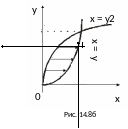
Если область D
рассматривать как правильную в направлении
Ox (рис. 14.8б), то (см.
(14.4))
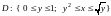 .
По формуле (14.6)
.
По формуле (14.6)
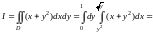
=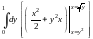 =
=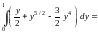
=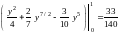 .
.
14.2.4. Замена переменных в двойном интеграле
Пусть функции
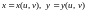 осуществляют взаимно однозначное
непрерывно дифференцируемое отображение
области P плоскости
осуществляют взаимно однозначное
непрерывно дифференцируемое отображение
области P плоскости
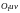 на область S плоскости
на область S плоскости
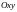 .
Тогда существует обратное непрерывно
дифференцируемое отображение
.
Тогда существует обратное непрерывно
дифференцируемое отображение
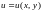 ,
,
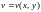 области S на область
P, если якобиан
преобразования
области S на область
P, если якобиан
преобразования
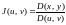 =
=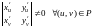 .
.
Величины u и v можно рассматривать как прямоугольные координаты для точек области P и в то же время как криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат u и v сохраняет постоянное значение, образуют координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть есть дифференцируемое преобразование области P из плоскости на область S из плоскости . Тогда справедливо равенство
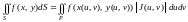
(14.7)
З а м е ч а н и е. Равенство (14.7) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
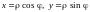 (14.8)
(14.8)
преобразуют
полярные координаты
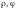 точки в декартовы координаты этой точки
и переводят область
точки в декартовы координаты этой точки
и переводят область
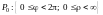 (или область
(или область
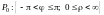 )
на всю плоскость Oxy.
)
на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам:
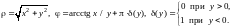
Фиксируя
в последних формулах
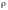 и
и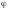 ,
получим координатные линии из разных
семейств: окружность с центром в точке
,
получим координатные линии из разных
семейств: окружность с центром в точке
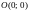 и
луч, исходящий из точки
.
и
луч, исходящий из точки
.
Якобиан преобразования
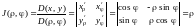 ,
,
и формула (14.7) принимает вид:
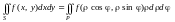
(14.9)
Рекомендация.
К полярным координатам целесообразно
переходить, когда в подынтегральное
выражение или в уравнения границы
области интегрирования входит комбинация
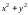 .
.
В некоторых случаях
при вычислении двойного интеграла
удобно перейти от
декартовых координат к обобщенным
полярным координатам
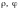
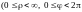
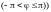 по формул
по формул
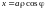 ,
,
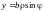 ,
(14.10)
,
(14.10)
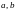 –
постоянные,
–
постоянные,
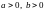 .
Тогда
.
Тогда
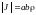 ,
,
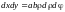 . (14.11)
. (14.11)
Пример 6.
Записать в полярной системе координат
область S, заданную
в декартовой системе координат
неравенством
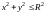 (круг радиуса R с
центром в точке
(круг радиуса R с
центром в точке
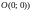 .
.
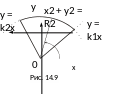 Перейдем от
декартовых координат x,
y к полярным
по формулам
Перейдем от
декартовых координат x,
y к полярным
по формулам
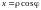 ,
,
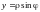 .
Подставим x и y
в исходное неравенство, получим:
.
Подставим x и y
в исходное неравенство, получим:
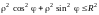 или
или
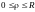 .
На координату
дополнительных ограничений не
накладывается, поэтому
.
На координату
дополнительных ограничений не
накладывается, поэтому
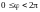 (или
(или
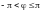 ).
В
полярной системе координат круг
записывается неравенствами:
).
В
полярной системе координат круг
записывается неравенствами:
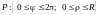 .
.
Пример 7. Записать
в полярной системе координат область
S – часть круга,
ограниченную линиями
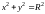 ,
,
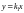 ,
,
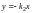 (
(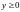 ),
),
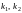 – постоянные,
– постоянные,
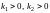 .
.
Изобразим область S (рис. 14.9). Запишем заданные линии в полярных координатах, которые связаны с декартовыми формулами , :
1)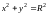
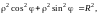
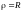 ;
;
2)
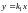
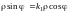 ,
,
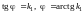 ;
;
3)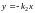
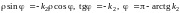 .
.
Область
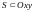 переходит в область
переходит в область
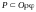 .
.
В
полярной системе координат заданная
область определяется системой неравенств:
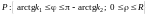 .
.
Пример
8. Вычислить двойной интеграл
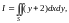 S – множество точек,
удовлетворяющих неравенству
S – множество точек,
удовлетворяющих неравенству
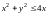 .
.
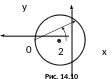 Границей области
является линия
Границей области
является линия
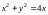 или
или
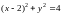 – окружность радиуса 2 с центром в точке
– окружность радиуса 2 с центром в точке
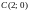 (рис. 14.10).
(рис. 14.10).
Наличие
в уравнении границы комбинации
наводит на мысль,
что для вычисления
двойного интеграла удобно перейти
к полярным координатам
по формулам
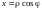 ,
,
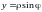 ,
,
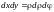 .
Уравнение границы
.
Уравнение границы
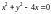 переходит в уравнение
переходит в уравнение
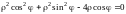 или
или
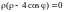 .
Отсюда
= 0 (соответствует полюсу O)
и
.
Отсюда
= 0 (соответствует полюсу O)
и
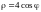 – уравнение окружности. Так как всегда
– уравнение окружности. Так как всегда
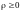 (по смыслу ),
то из
следует
(по смыслу ),
то из
следует
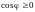 ,
отсюда получаем
,
отсюда получаем
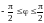 (этот же результат можно усмотреть из
рисунка). Итак, в полярных координатах
область интегрирования есть
(этот же результат можно усмотреть из
рисунка). Итак, в полярных координатах
область интегрирования есть
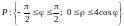 .
Тогда по формуле (14.9)
.
Тогда по формуле (14.9)
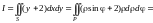
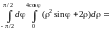
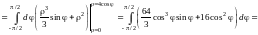
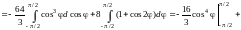
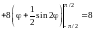 .
.
Пример
9. Вычислить
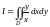 ,
где
,
где
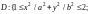
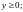
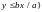 .
.
Область D
ограничена линиями:
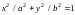 –
эллипс с полуосями a
и b,
–
эллипс с полуосями a
и b,
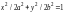 –
эллипс с полуосями
–
эллипс с полуосями
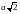 и
и
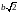 ,
y = 0 – прямая (ось
Ox),
,
y = 0 – прямая (ось
Ox),
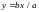 –
прямая (рис. 14.11).
–
прямая (рис. 14.11).
Анализ границы области указывает на целесообразность перехода к обобщенным полярным координатам по формулам (14.10),
(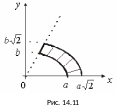 14.11):
14.11):
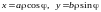 ,
,
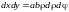 .
Уравнения границы области в координатах
будут: 1)
.
Уравнения границы области в координатах
будут: 1)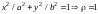 ;
;
2)
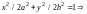
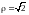 ;
;
3)
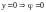 ;
4)
;
4)
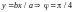 .
Итак, область интегрирования в координатах
.
Итак, область интегрирования в координатах
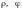 есть
есть
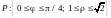 .
.
Тогда
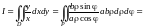
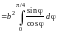
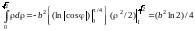 .
.
