Г л а в а 14
Кратные, КРИВОЛИНЕЙНЫЕ, ПОВЕРХНОСТНЫЕ
Интегралы
14.1. Определение кратного интеграла.
Определение двойного и тройного
интеграла
Пусть: 1) в ограниченной
замкнутой области
«объема» v(E)
задана ограниченная функция
;
2)
– разбиение области
на подобласти
с объемами
и
диаметрами
,
– диаметр разбиения; 3) зафиксируем
точки
,
;
4) построим интегральную сумму
.
Определение.
Конечный предел I
интегральной суммы
при
называется m-кратным
интегралом от функции f
по области E и
обозначается
или
.
(14.1)
Таким образом, по определению
.
(14.2)
В
этом случае функция
называется интегрируемой в E.
При m
= 2 (m = 3) для
ограниченной функции f
в замкнутой области
)
кратный интеграл (14.1) называется двойным
(тройным) интегралом, а
соответствующее определение (14.2) примет
вид
,
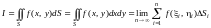где
точка
,
где
точка
.
14.2. Двойные интегралы
14.2.1. Области на плоскости
Определение.
Область
назовем правильной в направлении
Oy, если прямая,
проходящая через любую внутреннюю точку
из S параллельно оси
Oy, пересекает границу
области ровно в двух точках (рис. 14.1).
Область S
будет правильной в направлении Oy
, если существуют функции
и
,
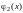определенные и непрерывные на [a;
b] и такие, что координаты
точек, принадлежащих (S),
удовлетворяют условиям:
;
тогда символически можно записать:
.
(14.3)
Область
S будет правильной
в направлении Ox,
если существуют функции
и
,
определенные и непрерывные на [c;
d] и такие, что координаты
точек, принадлежащих S
, удовлетворяют условиям:
(рис.
14.2); тогда символически
.
(14.4)
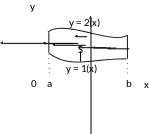
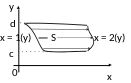
Рис. 14.1 Рис. 14.2
Область называется правильной, если она правильная в обоих направлениях Ox и Oy.
Пример
1. Область
S задана
уравнениями границы:
.
Изобразить указанную область и записать как правильную.
Область
S
– треугольник, ограниченный прямыми
(рис. 14.3). Точки пересечения прямых есть
O(0; 0), A(2; 1),
B(2; 2).
а) Область S
– правильная в направлении Oy
и любая прямая L,
проходящая через внутреннюю точку
области, пересекает
прямую
и прямую
.
Поэтому в силу
(14.3) область задается
системой неравенств:
.
б) Эта же область
является правильной и в направлении
Ox, но для задания ее
системой неравенств необходимо область
S разбить на две части
S1 и S2
(рис. 14.4). Выразим в уравнениях границы
x через независимую
переменную y : OB:
x = y,
OA: x
= 2y. Для определения
границ изменения переменной y
проведем прямые, параллельные оси Ox.
Прямая L1
пересекает прямую OB:
x = y
и прямую OA: x
= 2y; прямая
L2 пересекает
прямую OB:
x
= y
и прямую AB:
x
= 2. Итак,
и в силу (14.4)
,
.
Пример 2. Точки
из области D удовлетворяют
неравенству
(a > 0) , т.е.
.
Изобразить данную область и записать
как правильную.
Преобразуя
неравенство
,
получим
.
Геометрически область D
есть круг радиуса a/2
c центром в точке С(a/2;
0). Из уравнения границы
следует
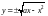или
.
Область D может быть
записана как правильная в направлении
Oy (любая прямая,
проходящая через внутреннюю точку D
параллельно Oy,
пересекает полуокружность
и
полуокружность OML:
(рис. 14.5)), в силу (14.3)
.
Область
D можно записать как
правильную в направлении Ox
(прямая, проходящая через внутреннюю
точку D параллельно
Ox, пересекает
полуокружность
и полуокружность
+
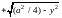(рис. 14.6)), и в силу (14.4):
.
Рис. 14.5 Рис. 14.6