Методические указания к решению

Внутренний диаметр трубопровода d следует подбирать исходя из формулы Дарси для потерь по длине :

где - коэффициент гидравлического трения,

- средняя скорость потока в трубопроводе,

где S – площадь поперечного сечения потока в трубопроводе:

Коэффициент определяется по формулам:

Ламинарный режим Re<2300:

Турбулентный режим Re>2300

соответствующий закону сопротивления гладкой стенки.

Число Рейнольдса:

В преобразованном виде формула записывается следующим образом:

Задаваясь значениями d=(10…25)* м, определяем среднюю скорость , число , затем коэффициент гидравлического трения . Подставляя значения d и в уравнение, вычисляем его правую часть. Левая часть уравнения определяется, исходя из баланса давления жидкости в трубопроводе:

Поскольку , получаем:

Подобным образом проводим дальнейшие расчеты и сводим их в табл.2.

Таблица 2

d ,м

S, м2

V, м/с

Re

∆p1,МПа

Далее решаем эту задачу графоаналитическим методом.

Строим график , проецируем точку , полученную в левой части уравнения и находим искомую величину

Практическая работа №2 Расчет напорной гидравлической системы

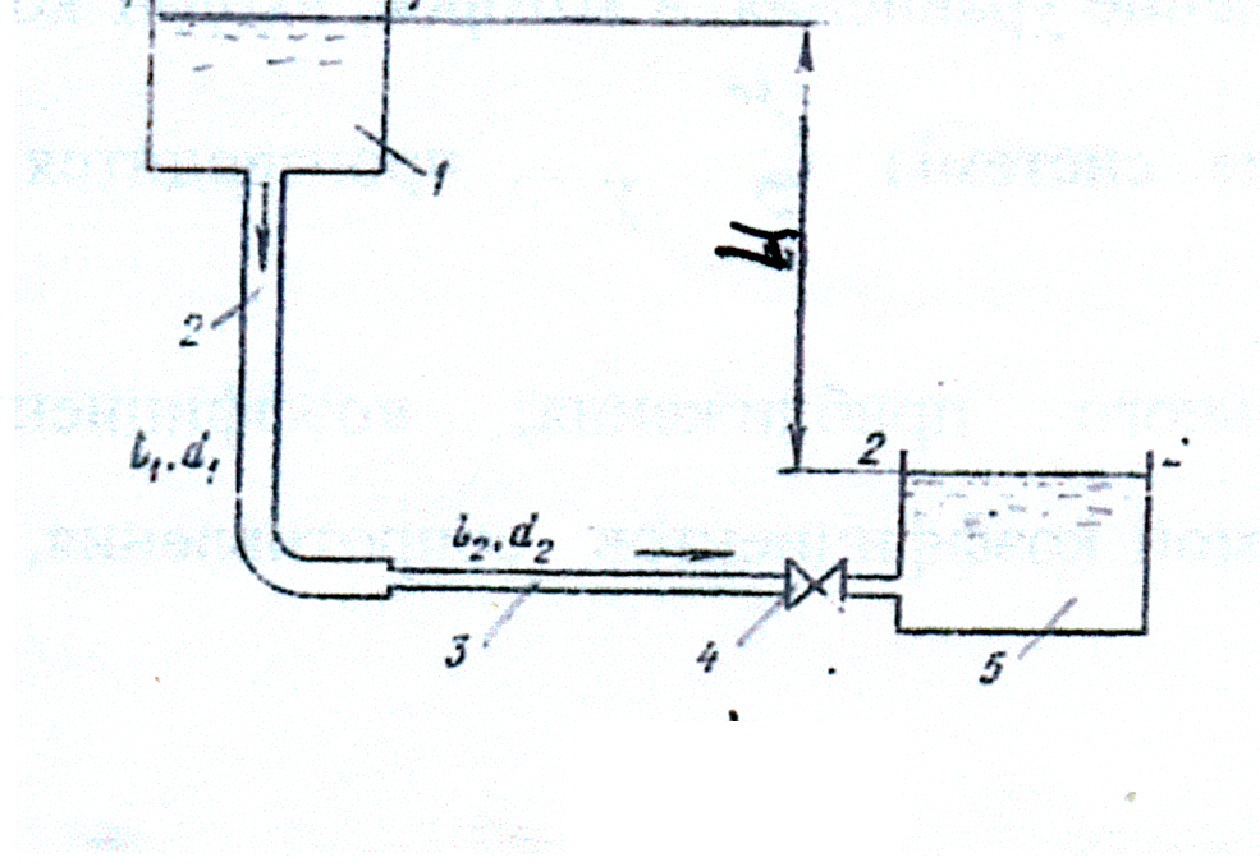
Рис.2. Схема напорной гидравлической системы

Напорная гидравлическая система состоит из двух открытых резервуаров 1 и 5, вертикального 2 и горизонтального 3 трубопроводов. На горизонтальном трубопроводе установлен вентиль 4. При постоянной разности уровней вода из резервуара 1 поступает в резервуар 5. Заданы (табл.3) длины трубопроводов и внутренние диаметры и , коэффициент сопротивления вентиля , разность уровней Z.

Определить расход воды в системе.

Таблица 3

Параметры\ Цифра шифра	Варианты и исходные данные
	00	01	02	03	04	05	06	07	08	09
Н,м \предпоследняя	4,0	2,5	4,5	3,5	3,0	2,7	4,2	5,0	4,5	3,5
. \последняя	4,5	3,8	5,0	4,2	3,5	4,0	5,1	4,7	3,9	4,1
мм \последняя	32	40	50	25	20	32	50	40	25	32
\предпоследняя	4,0	5,2	4,8	4,5	5,1	3,8	5,5	4,9	6,1	4,7
\последняя	9,0	7,9	10	8,4	7,0	8,0	10,2	9,4	7,8	8,2
мм \последняя	15	20	25	13	10	20	32	25	15	15

Методические указания к решению

Расход воды Q в системе определяется по величине средней скорости потока в сечении трубопровода 3 и площади сечения

Для определения средней скорости необходимо применить уравнение Бернулли для контрольных сечений 1-2 и 2-2 (рис. 4.2) с учетом гидравлических потерь в трубопроводе и наметив плоскость сравнения 0-0, совпадающей с уровнем в баке 2 и приняв значения средних скоростей в контрольных сечениях равными нулю.

Гидравлические потери в трубопроводе состоят из потерь по длине в трубах 2 и 3 - _, и в местах потерь: на входе в трубопровод из бака 1- , на повороте трубопровода - , в сужении трубопровода - в вентиле - и на выходе из трубопровода в бак 2 -

Выразив потери напора по длине по формуле Дарси

и местные по формуле Вессбаха

м ,,

составим их сумму, вынося общий множитель за скобки. В скобках получим коэффициент сопротивления системы равный сумме коэффициентов сопротивления по длине и , коэффициентов местных сопротивлений: на выходе из бака 1 - , на повороте трубопровода - , на сужении трубопровода - , в вентиле - , на входе в бак 2 - . Коэффициенты , и являются приведенными (к скорости в трубе 3), т.е. умноженными на отношение площадей сечения труб - = .

Численные значения коэффициентов местных сопротивлений: =0.5; =1,1; =0,5 [1- ]; =1. Коэффициент сопротивления по длине равен , где гидравлический коэффициент трения в первом приближении определяется по формуле Прандтля – Никурадзе:

,

причем эквивалентную шероховатость стенки можно считать равной 0,5 мм.

Порядок вычислений

1. Определяем коэффициенты гидравлического трения и .

2. Вычисляем приведенные коэффициенты сопротивления:

; ; и коэффициенты и .

3. Вычисляем коэффициент сопротивления системы :

4. Записываем уравнение Бернулли в общем виде и в преобразованном виде:

.

В уравнении (4.6) ; (атмосферное давление); (из условия неразрывности течения) ;

, - гидравлические потери.

Уравнение Бернулли в преобразованном виде:

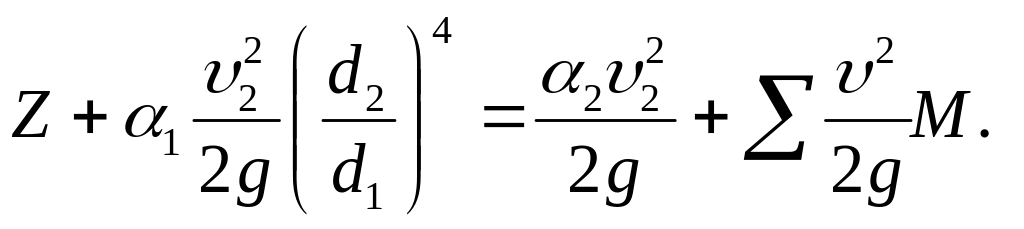
Приняв значения коэффициентов кинетической энергии и равными единице, решаем уравнение

Z = [1 - + ] м, откуда

Обозначим

- коэффициент скорости.

Определим его численные значения и скорость .

По формуле определяется расход .

5. Проверка вычисленных значений коэффициентов и .

Коэффициенты и соответствуют так называемой квадратичной области сопротивления при турбулентном течении. Здесь эти коэффициенты зависят только от относительной шероховатости стенки трубы - . Эта область находится на графике зависимости λ= ( , приведенном в [2] в диапазоне Re > , где Re - число Рейнольдса, определяемое по формуле

Определив по расходу и сечению трубы скорость и рассчитав числа Рейнольдса и , сопоставляем эти числа с предельным значением Re>

Если полученные числа Re >, то уточнений не требуется. В противном случае надлежит вычислить коэффициенты и по графику