46. Способы построения эпюры m, n, q в методе сил после определения всех неизвестных метода сил.

Построение эпюры окончательных поперечных сил осуществляется по формуле:

П ервое слагаемое ( ) учитывается только на участке, где действует равномерно распределённая нагрузка. Если смотреть на стержень с равномерно распределенной нагрузкой таким образом, что она будет действовать сверху вниз, то на данном участке в крайнем в крайнем левом сечении всегда будет ( ), а в крайнем правом ( ).

Второе слагаемое берём из эпюры моментов. Знак «+» принимается том случае если совмещение оси стержня с касательной к эпюре изгибающих моментов по кратчайшему расстоянию осуществляется по часовой стрелке, в противном случае знак «-» .

Построение окончательной эпюры продольных сил осуществляется способом вырезания узлов из эпюры поперечных сил и составлением уравнений равновесия на оси Х и У.

47. Симметричной называется рама, которая обладает геометрической и упругой симметрией относительно оси.

Симметричными называют эпюры, в которых соблюдается симметрия относительно некоторой оси в равенстве изгибающих моментов и в расположении растянутых волокон. Кососимметричная эпюра- эпюра, в которой соблюдается равенство изгибающих моментов и не соблюдается расположение растянутых волокон. Соответственно этим усилиям неизвестные метода сил называют симметричными и кососимметричными.

Неиз

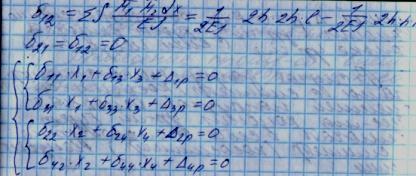
Для симметричных рам с сим-ой (кососим.) внешней нагрузкой с-ма канонич. ур-ий может быть представлена в виде двух незав-х с-м одна из которых будет включать симметрич. весн., др.-только кососимметрич. Неизв.

48. К каким упрощениям приводит выбор для симметричной статически неопределимой рамы симметричной основой системы (о.С.) метода сил с симметричными и коссосимметричными неизвесными.

1 Разбиение с-мы канонич. ур-ий на две незав-ые с-мы для симметричных рам загруж. симметрично (кососимметрич. Внешн. Нагрузки).

Симметричными называют эпюры, в которых соблюдается симметрия относительно некоторой оси в равенстве изгибающих моментов и в расположении растянутых волокон.

Кососимметричная эпюра- эпюра, в которой соблюдается равенство изгибающих моментов и не соблюдается расположение растянутых волокон.

Соответ. этим усилиям неизвестные метода сил называют симметричными и кососимметричными.

Для симметричных рам с сим-ой (кососим.) внешней нагрузкой с-ма канонич. ур-ий может быть представлена в виде двух незав-х с-м одна из которых будет включать симметрич. Неизвесн., др.-только кососимметрич. Неизв.

49. Как упростится расчет симметричной рамы, загруженной симметричной внешней нагрузкой, при выборе для расчета симметричной основной системы (О.С.) метода сил с симметричными и коссосимметричными неизвесными.

В случае загружения симметричной рамы симметричной внешней нагрузкой основная система канонических уравнений будет включать только уравнения с симметричными неизвестными, т.к.

50. Как упростится расчет симметричной рамы, загруженной кососимметричной внешней нагрузкой, при выборе для расчета симметричной основной системы (О.С.) метода сил с симметричными и коссосимметричными неизвесными.

В случае загружения симметричной рамы кососимметричной внешней нагрузкой, основная система канонических уравнений будет включать только уравнения с кососимметричными неизвестными, т.к.

51 В каких случаях для основной системы метода сил необходима группировка неизвестных, как и для чего она выполняется

Для с-м, в котор. Неиз-ые метода сил расположены не на оси симметрии для упрощения расчета вып-ют группировку неизвестных:

52 Как представить произвольную нагрузку, действующую на симметричную раму, в виде суммы симметричной и кососимметричной нагрузок

53. Запишите допущения, используемые в расчетах статически неопределимых рам методом перемещений.

Пренебрегают влиянием продольных и поперечных сил на деформации стержней учитывая лишь деформации изгиба.

Проекция деформированного стержня на его первоначальное положение равняется первоначальной длине.

Все жесткие узлы системы после ее деформации остаются неизменными, т.е. сохраняют равенства узлов между стержнями, которые соединены в узле.

Тангенс углов поворота стержней в силу их малости считают равными самим углам.