Средняя гармоническая, её назначение и сущность, виды и порядок расчёта, область применения
Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
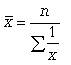(5.6)
К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:
В
статистической практике чаще
используется
гармоническая
взвешенная, формула которой имеет вид
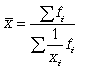(5.7)
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров:
Вид товара |
Цена за единицу, руб. |
Сумма реализаций, руб. |
а |
50 |
500 |
б |
40 |
600 |
с |
60 |
1200 |
Получаем
Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:
Средняя геометрическая, её назначение и порядок расчёта, область применения
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.
Для простой средней геометрической
Для взвешенной средней геометрической
(5.9)
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).
Формула простой средней квадратической
(5.10)
Формула взвешенной средней квадратической
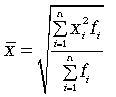(5.11)
В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:
а) установление обобщающего показателя совокупности;
б) определение для данного обобщающего показателя математического соотношения величин;
в) замена индивидуальных значений средними величинами;
г) расчет средней с помощью соответствующего уравнения.
Мода и медиана как разновидности средних. Их сущность и назначение
Средние арифметическая и гармоническая являются обобщающими характеристиками совокупности по тому или иному варьирующему признаку. Вспомогательными описательными характеристиками распределения варьирующего признака являются мода и медиана.
Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Медианной в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.
Мода и медиана в отличии от степенных средних являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.
Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров, размер ботинок, пользующийся наибольшим спросом у потребителей, и т.д., в этих случаях прибегают к моде.
Медиана интересна тем, что показывает количественную границу значение варьирующего признака, которую достигла половина членов совокупности. Пусть средняя заработная плата работников банка составила 650000 руб. в месяц. Эта характеристика может быть дополнена, если мы скажем, что половина работников получила заработную плату 700000 руб. и выше, т.е. приведем медиану. Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности.