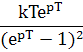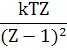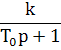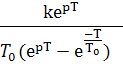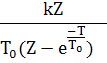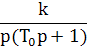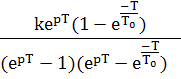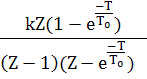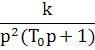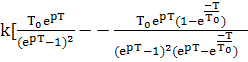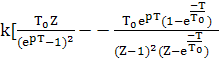- •1)Расчет коэффициентов усиления исходя из заданного значения добротности.
- •2)Синтез следящей сау методом последовательной оптимизации контуров.
- •3)Блок – схема управляющего устройства следящей сау.
- •4)Синтез следящей сау методом модального управления.
- •Другой вариант схемы, построенной методом модального управления
- •5)Комбинированная позиционная сау(позиционные у с переменно структурой)
- •6)Дискретные сау
- •Квантование сигнала по времени.
- •Квантование сигнала по уровню.
- •Комбинированное квантование.
- •7)Дискретное преобразование Лапласса, z-преобраз,d-преобразования
- •8)Основные свойства дискретного преобразования Лапласа
- •9)Передаточная функция одноконтурной импульсной сау
- •10)Передаточная функция двухконтурной импульсной сау
- •11)Переход от непрерывной передаточной функции к дискретной
- •12)Устойчивость импульсных сау
- •Если внутри окружности – с-ма устойчива
- •Если на границе окр-ти – с-ма на границе устойчивости
- •13) Критерий устойчивости Шуркона
- •14) Частотный критерий Найквиста
- •15)Синтез цуу.
- •16)Расчет динамических характеристик импульсных сау.
- •17)Синтез последовательного дискретного корректирующего устройства.
- •18)Алгоритм реализации дискретного корректирующего устройства на эвм
- •19)Синтез непрерывного последующего корректирующего устройства
- •20)Нелинейные сау. Метод гармонической линеаризации
- •21)Аналитический метод определения автоколебаний для систем с однозначной нелинейностью
- •2 2)Метод Гольдфорба или графо-аналитический метод определения амплитуды автоколебаний
- •23)Вынужденные колебания в релейных сау
- •24)Система экстремального управления (сэу)
- •25)Принципы построения систем экстремального управления
- •2 6)Сэу с непрерывным поиском сигнала
- •27)Динамика систем экстремального управления
- •28)Системы оптимальные по быстродействию (сопб)
- •29)Оптимальные по быстродействию траектории движения.
- •30 Построение разомкнутых сау. Определение момента переключения методом сшивания траектории
- •31)Построение замкнутых систем оптимальных по быстродействию.
- •32)Квазиоптимальное управление.
- •33)Самонастраивающаяся система управления. Принципы построения самонастраивающихся сау.
- •34)Применение ортогональных фильтров для построения самонастраивающихся систем:
Комбинированное квантование.
Комбинированное квантование заключается в том, что сигнал может принимать только сигналы разрешенных уровней и может изменяться в разрешенные моменты времени.
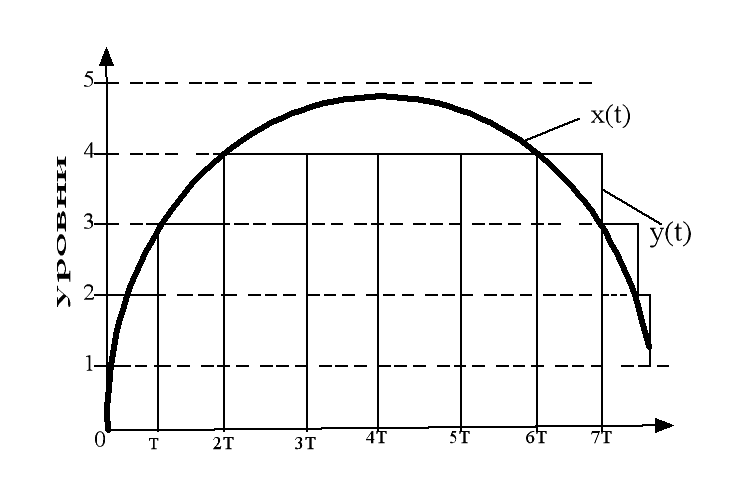
АЦП – аналого-цифровой преобразователь.
В зависимости от вида квантования системы делятся на:
1. импульсные – это когда один из сигналов квантуется по времени;
2. релейные системы – это когда хотя бы один из сигналов квантуется по уровню, задатчик можно рассматривать как релейную систему;
3. цифровые системы – это когда хотя бы один из сигналов квантуется по времени и по уровню (комбинированное квантование).
Структурная схема цифровой системы (см. рис.):
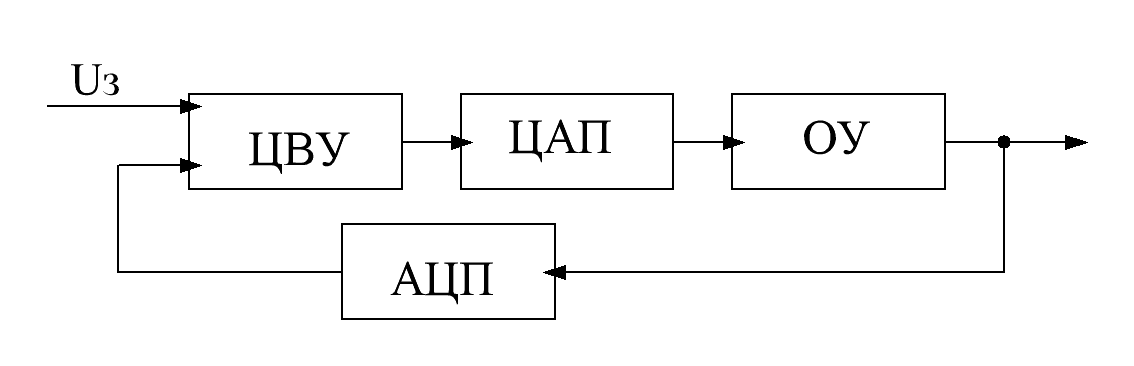
ЦВУ – цифровое вычислительное устройство.
Цифровая система является нелинейной САУ из-за наличия квантования по уровню.
При большой развратности АЦП и ЦВУ квантованием можно пренебречь.
Импульсный элемент преобразует непрерывный сигнал в дискретный, т. е. непрерывный сигнал заменяем последовательностью импульсов. Импульсный элемент можно представить как (см. рис.):
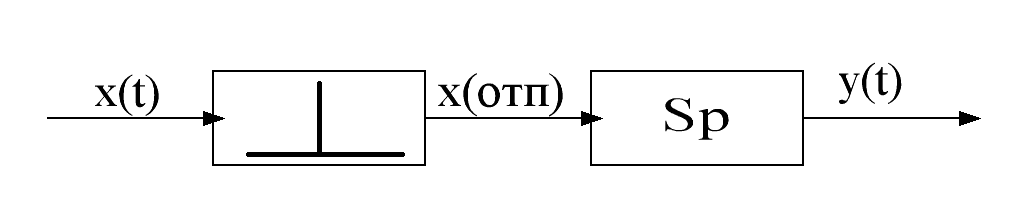
где 1 – простейший импульсный элемент, он преобразовывает импульсный сигнал в решетчатый.
2 – формирователь, он может строится как АИН и ШИП(ШИМ).
Ширина импульсов постоянная, а амплитуда нет.
Широтно-импульсная модуляция.
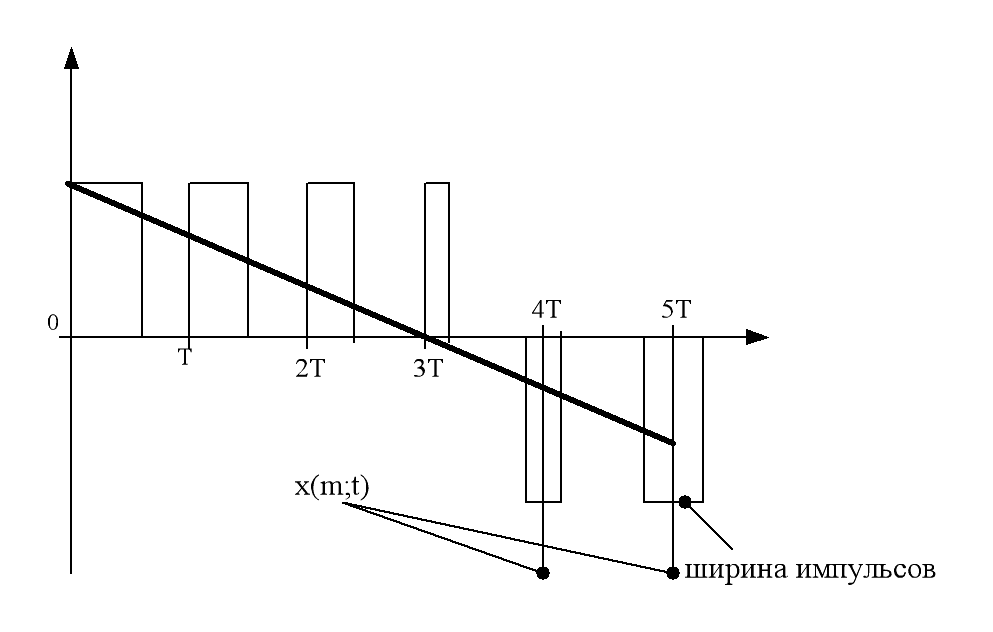
Амплитуда импульсов постоянная, но изменяется их ширина.
Ширина пропорциональна значению непрерывного сигнала в моменты квантования по времени.
7)Дискретное преобразование Лапласса, z-преобраз,d-преобразования
Дискретное
преобразование Лапласса служит для
определения изображения решетчатой
функции ![]()
![]() (1).
(1).
Соотнош.
(1),устанавливающее связь между решетчатой
фн-ей и ее изображением, называеться
дискретным преобразованием Лапласса
или D-преобразованием.![]() ,
,
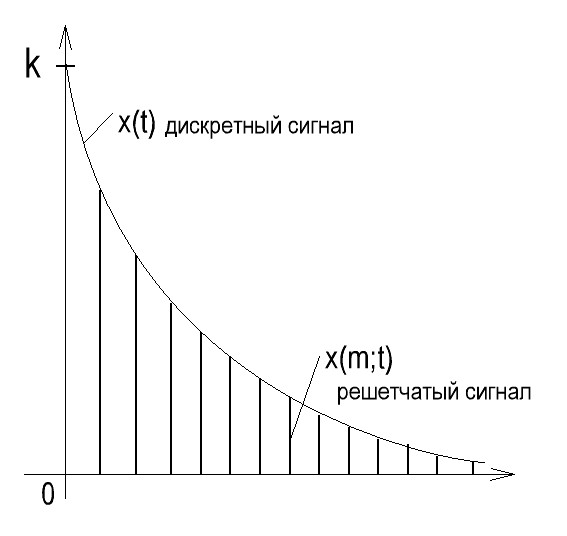 x(0)-нач.значение
непрерывн. сигнала;
x(0)-нач.значение
непрерывн. сигнала; ![]() -
частота квантования сигнала.
-
частота квантования сигнала.
Соотношение(2) устанавливающее связь между изображением непрерывного и дискретн. сигнала также наз. Д-преобразованием.
Найти изображение решетчатого сигнала используя (1)
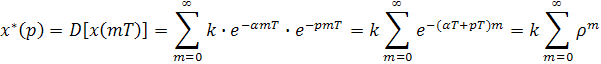
![]() (3)
(3)
![]() -ряд
геометр. прогрессии;
–сумма ряда геометр прогрессии; Домножим
числитель и знаменатель на
-ряд
геометр. прогрессии;
–сумма ряда геометр прогрессии; Домножим
числитель и знаменатель на ![]()
![]() (4);
Из (3) и (4) видно, что изображ. непрерывного
сигнала зависит от (p),
а решетчатого от
(4);
Из (3) и (4) видно, что изображ. непрерывного
сигнала зависит от (p),
а решетчатого от
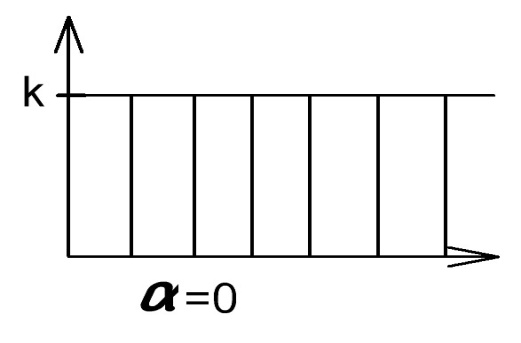 Ступенчатый
сигнал
Ступенчатый
сигнал
![]() ;
;![]()
В
ТАУ помимо D-преобразования
сущ. и Z-преобразование.
![]()
![]() ;
;![]() .
Принципиально нового Z-преобраз.
по отношению к D
не вносят, просто более удобная форма
записи.
.
Принципиально нового Z-преобраз.
по отношению к D
не вносят, просто более удобная форма
записи.
8)Основные свойства дискретного преобразования Лапласа
Свойства Д и D преобразований совпадают
1.
![]() ;
;
2. Дискретн. преобр. суммы равно сумме дискретных преобразований
![]() ;
;
3.
![]()
4Изображение
дискрет. сигнала можно выносить за знак
дискр. сигнала ![]() ;
;![]()
5![]() можно
выносить за знак Д преобразования
можно
выносить за знак Д преобразования
![]()
№ |
x(p) |
|
|
1 |
k |
K |
K |
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|