2.5.Распределение Максвелла

В газе, находящемся в состоянии равновесия, устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям. Пусть имеетcя N молекул, причем dN(v) - число молекул, имеющих скорость в интервале от v до dv. Как показал Максвелл, для идеального газа справедлив закон распределения молекул идеального газа по скоростям (распределение Максвелла)

dN(v)= N4[m/2kT]^3/2v²exp[-mv²/2kT]dv = Nf(v),

(5)

где f(v) = 4[m/2kT]^3/2v²exp[-mv²/2kT] называется функцией распределения молекул по скоростям и она показана на рис.3. Относительное число молекул, скорости которых лежат в интервале от v до v+dv, равна площади dS = N(v)/N, заштрихованной на рис.3. Площадь под кривой f(v) равна единице, т.е. функция f(v) нормирована на единицу

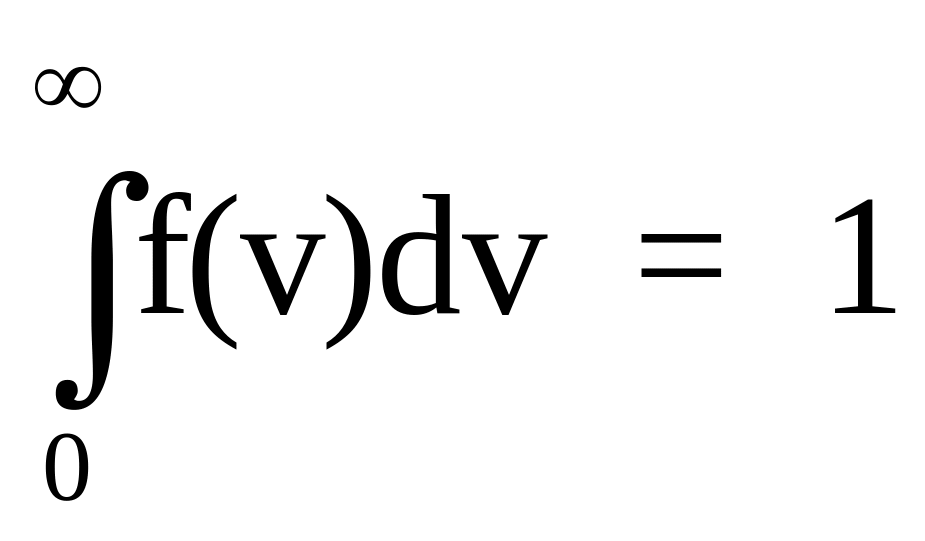
Скорость, при которой функция распределения f(v) максимальна, называется наиболее вероятной скоростью v_в= (эта скорость находится путем дифференцирования функции f(v) по аргументу v и приравнивания результата нулю). Видно, что повышение температуры смещает распределение молекул по скоростям вправо, увеличивая v_в, однако площадь под кривой f(v) остается неизменной. Иными словами, при повышении температуры кривая f(v) растягивается, понижается и смещается в область больших v (рис.4).

f(v) f(v)

dS=dN(v)/N T₁

T₂

Рис.3 T₂>T₁ Рис.4

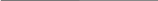v_в <v_кв> v v

dv <v>

Функция f(v) позволяет найти среднюю (арифметическую) скорость молекул <v> = .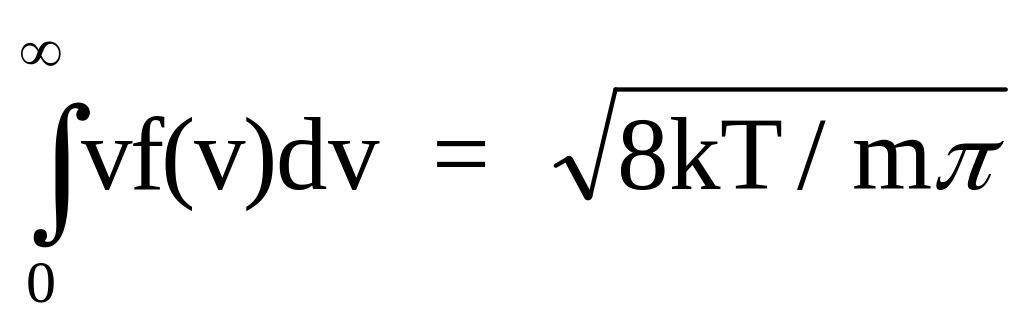

Таким образом, скорости, характеризующие состояние газа: наиболее вероятная v_в = , средняя <v> = = 1.13v_в и средняя квадратичная <v_кв> = = 1.22v_в.

Из распределения молекул по скоростям (5) можно найти распределение молекул по кинетическим энергиям (по энергиям теплового движения) (распределение Максвелла-Больцмана) (для этого следует перейти от переменной v к переменной E=mv²/2): число молекул, имеющих кинетическую энергию, заключенную в интервале энергий от E до E+dE, равно dN(E) = (2N/ )(kT)^-3/2E^1/2exp(-E/kT)dE = Nf(E), где f(E) = (2/ )(kT)^-3/2E^1/2exp(-E/kT) называется функцией распределения молекул по кинетическим энергиям (по энергиям теплового движения), а средняя кинетическая энергия <E> молекулы идеального газа <E_k> = Ef(E)dE = 3kT/2, т.е. получили результат, совпадающий с (4). Функция f(E) приведена на рис.3а и 4а - она схожа с функцией f(v), но несколько растянута в области высоких энергий.