
- •2 Семестр.
- •Лектор: Сухинин м. Ф.
- •Канонические и нормальные системы оду. Порядок системы. Сведение системы к одному уравнению и наоборот.
- •Лемма Арцелы (критерий компактности).
- •Ломаные Эйлера и теорема Пеано.
- •Теорема о единственности решения задачи Коши для систем оду. Следствие для оду n-го порядка. Случай линейного уравнения и линейной системы.
- •Лемма о равномерной непрерывности.
- •Непрерывность решения системы оду по начальным данным и параметру.
- •2) , , : & Это следует из открытости множества, непрерывности в точке и условия . Выберем , .
- •Линейная зависимость и независимость вектор-функций. Определитель Вронского.
- •Фундаментальная система решений (фср) для линейной однородной системы оду. Существование фср и их взаимосвязь. Общее решение линейной однородной неоднородной системы.
- •Резольвента линейной системы оду и ее свойства.
- •Построение линейной, однородной системы по известной фср. Формула Лиувилля.
- •Линейные системы с постоянными коэффициентами и методы их решения Случай не нормализуемой системы.
- •Нормальные линейные системы с постоянными коэффициентами и методы их решения
- •Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости.
- •Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант.
- •Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
- •Лемма Адамара.
- •Дифференцируемости решения системы оду по начальным данным и параметру.
- •Первые интегралы систем дифференциальных уравнений. Задание общего решения системы с помощью полной системы первых интегралов.
- •Существование полной системы первых интегралов
- •Линейные однородные УрЧп первого порядка. Связь с первыми интегралами соответствующей системы оду. Замечание о квазилинейных уравнениях.
- •Квазилинейные УрЧп первого порядка. Две леммы о характеристиках.
- •Теорема о существовании единственного решения задачи Коши для квазилинейных УрЧп первого порядка в случае пространственных переменных.
- •По условию 4),
- •Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении.
- •Представление решения краевой задачи для уравнения Штурма-Лиувилля через функцию Грина. Выражение функции Грина и ее свойства.
Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
Теорема:
Рассмотрим систему
![]() (1). Пусть A
– постоянная
матрица с действительными
коэффициентами, размера
(1). Пусть A
– постоянная
матрица с действительными
коэффициентами, размера
![]() .
А
– n-мерная
действительная вектор-функция,
непрерывная по y
в полуцилиндре:
.
А
– n-мерная
действительная вектор-функция,
непрерывная по y
в полуцилиндре:
![]() ,
причем
,
причем
![]() – не зависит
от x,
где
– не зависит
от x,
где
![]() при
при
![]()
![]() .
.
Далее, пусть
![]() ,
где
– собственное
значение матрицы A
,
где
– собственное
значение матрицы A
![]() (некоторые
могут совпадать),
(некоторые
могут совпадать),
![]() .
Тогда нулевое
решение системы (1) асимптотически
устойчиво.
.
Тогда нулевое
решение системы (1) асимптотически
устойчиво.
Доказательство:
◄ Мы сведем эту теорему к проверке выполнимости условия леммы Ляпунова об асимптотической устойчивости.
По лемме: существует матрица T с условием : матрица будет иметь вид:
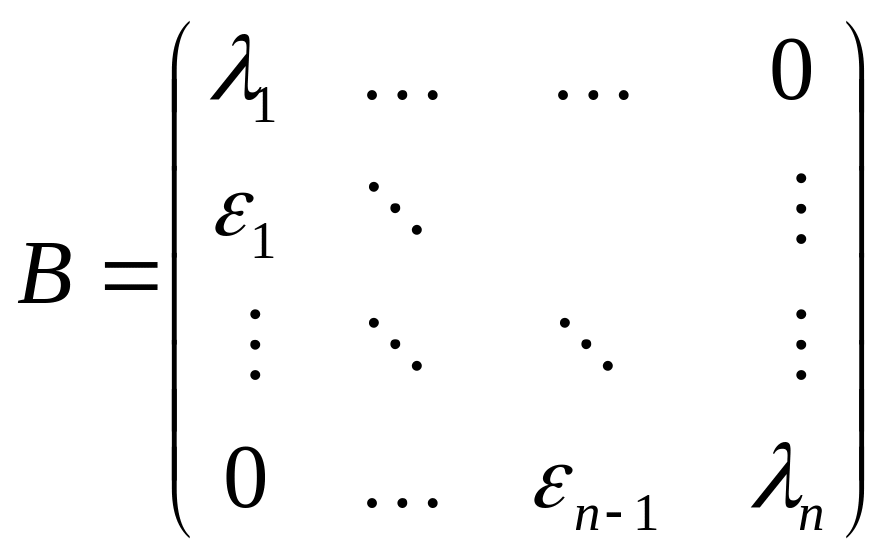 ,
,
где – собственное значение матрицы A (некоторые могут совпадать), а

(a – из условия теоремы). Положим , подставим в (1):
![]()
![]()
![]() (2).
(2).
Положим:
![]() ,
,
![]() .
Выполняется
условие леммы Ляпунова об асимптотической
устойчивости:
.
Выполняется
условие леммы Ляпунова об асимптотической
устойчивости:
1)
![]() – верно,
– верно,
2)
,
![]() ,
,
Осталось проверить условие:
3)
 .
.
Заметим, что
1)
![]() ,
,
2)
![]() ,
,
![]() .
.
Проверку условия 3) проведем в 3 этапа.
Сделаем некоторые оценки.
Пусть
 ,
,
 ,
,
тогда
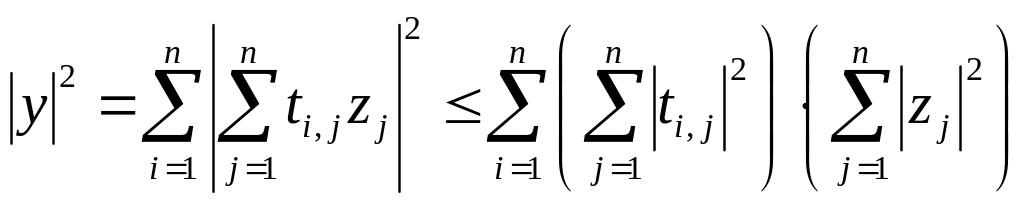
![]()
![]()
Аналогично
![]() .
.
![]() (3)
(3)
Запишем подробно систему (2):
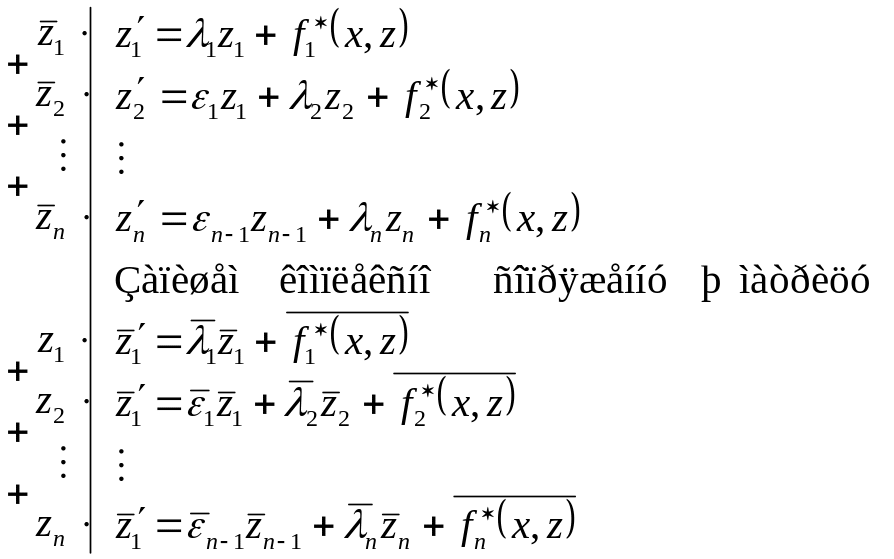
Пусть
![]() – решение
системы (1), а
– решение
системы (1), а
![]() – решение
системы (2), тогда
– решение
системы (2), тогда

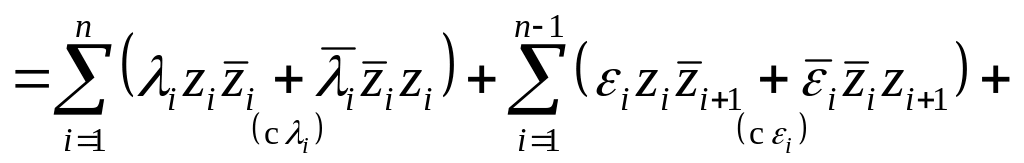
![]()
Оценим каждое
![]() .
.
 .
.

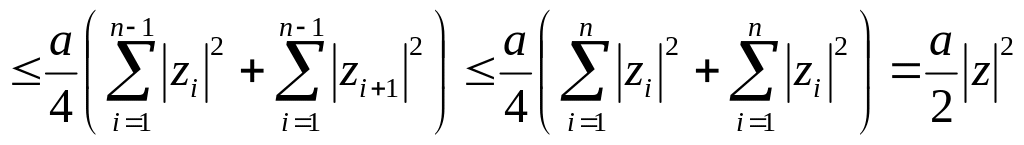 .
.
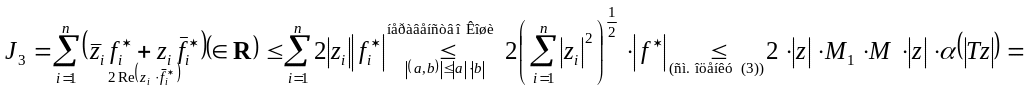
![]()
при достаточно малых
![]() ,
так как
при
,
так как
при
![]() (то есть
(то есть
![]()
![]() ,
,
![]()
![]() ).
).
Возьмем произвольную точку
![]() из полуцилиндра
из полуцилиндра
![]() ,
поскольку
через эту точку проходят интегральная
линия
(по теореме о
решения задачи
Коши), то в этой точке
будет
,
поскольку
через эту точку проходят интегральная
линия
(по теореме о
решения задачи
Коши), то в этой точке
будет
![]()
![]() +
+
![]() =
=
![]() ,
,
![]() .
.
То есть выполняется условие леммы Ляпунова об асимптотической устойчивости. Следовательно нулевое решение системы (1) асимптотически устойчиво. ►
Лемма Адамара.
Лемма:
Пусть
![]() – выпуклая
область в
– выпуклая
область в
![]() (то есть
(то есть
![]() отрезок,
соединяющий
и
отрезок,
соединяющий
и
![]() ).
).
![]() – метрическое
пространство, а функции
– метрическое
пространство, а функции
![]()
![]() и
и
![]() ,
,
![]() непрерывны
на
непрерывны
на
![]() .
.
Тогда
![]() ,
,
![]()
![]() ,
где
,
где
![]() непрерывна
на
непрерывна
на
![]() ,
.
,
.
Доказательство:
◄ По формуле Ньютона-Лейбница
![]() =
=![]() =
=
![]() =
=
 .
.
Непрерывность
![]() вытекает из
непрерывность интеграла по параметру
(по теореме из математического
анализа). ►
вытекает из
непрерывность интеграла по параметру
(по теореме из математического
анализа). ►
Замечание 1:
![]() (надо подставить
вместо
)
(надо подставить
вместо
)
Замечание 2:
Если
![]() имеет непрерывные
смешанные производные по
имеет непрерывные
смешанные производные по
![]() до порядка
до порядка
![]() включительно
и эти производные непрерывны на
,
включительно
и эти производные непрерывны на
,
![]() имеет непрерывную
смешанную производную по
и
имеет непрерывную
смешанную производную по
и
![]() (
(![]() )
до порядка
)
до порядка
![]() включительно
и эти производные непрерывны на
.
Это следует
из свойств интеграла (по теореме
из математического анализа).
включительно
и эти производные непрерывны на
.
Это следует
из свойств интеграла (по теореме
из математического анализа).
Дифференцируемости решения системы оду по начальным данным и параметру.
Теорема:
Пусть
– область в
.
![]() – отрезок, а
отображение
– отрезок, а
отображение
![]() непрерывно,
непрерывно,
![]() ,
,
![]() и
и
![]() так же непрерывны
на
так же непрерывны
на
![]() ,
.
Далее пусть
– решение
задачи Коши:
,
.
Далее пусть
– решение
задачи Коши:
![]() ,
,
определенное на
.
Функции
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
при некотором
.
Причем
,
при некотором
.
Причем
![]() ,
,
![]() ,
,
![]() .
.
Теперь
![]()
![]() Существует
единственное решение задачи Коши:
Существует
единственное решение задачи Коши:
![]() ,
,
определенное так же на
,
причем
![]() ,
дифференцируема
по
,
дифференцируема
по
![]() при
при
![]() и
и
![]() ,
удовлетворяет
условию
,
удовлетворяет
условию
![]()
![]() (5).
(5).
![]() (6)
(6)
Замечание: Формулы (5) и (6) получаются формальным дифференцированием по , подстановкой и дифференцированием по тождества

Доказательство:
◄ По теореме о
непрерывном решении по начальным данным
и параметру существует
единственное решение
задачи (3), (4),
определенное на
,
при достаточно
малых
![]() (то есть при
(то есть при
![]() ).
Далее
).
Далее
![]()
![]()
![]() ,
,
где
![]() непрерывна
при
непрерывна
при
![]() .
.
Положим
![]() ,
,
тогда
![]() является
решением задачи Коши
является
решением задачи Коши
![]() ,
,
![]()
![]()
функция
![]() ,
,
![]()
Далее
![]() .
По теореме о
непрерывности по начальным данным и
параметру
.
По теореме о
непрерывности по начальным данным и
параметру
![]() ,
где
,
где
![]() – решение
задачи
– решение
задачи
![]()
![]()
![]() и
– удовлетворяет
условиям (5), (6).
и
– удовлетворяет
условиям (5), (6).
Теорема доказана. ►
Замечание:
Все сказанное
справедливо при
близких к
нулю, а не только при
,
то есть
![]() удовлетворяет
уравнению
удовлетворяет
уравнению
![]() .
.
Это уравнение называется уравнением в вариациях.
Следствие 1:
Пусть в
предыдущей теореме
![]()
![]() и
и
![]() ,
тогда
,
тогда
![]() удовлетворяет
условиям
удовлетворяет
условиям
![]()
Следствие 2:
Пусть в
предыдущей теореме
![]()
![]()
![]() и
,
тогда
и
,
тогда
![]() удовлетворяет
условиям
удовлетворяет
условиям
![]()
![]() − матрица Якоби
и удовлетворяет условиям
− матрица Якоби
и удовлетворяет условиям
![]()
![]()
то есть
![]() – резольвента
линейной системы
– резольвента
линейной системы
![]() .
.
Следствие 3:
Пусть в
предыдущей теореме
![]()
![]() и
и
![]() ,
тогда
,
тогда
![]() удовлетворяет
условиям
удовлетворяет
условиям
![]()
