
- •2 Семестр.
- •Лектор: Сухинин м. Ф.
- •Канонические и нормальные системы оду. Порядок системы. Сведение системы к одному уравнению и наоборот.
- •Лемма Арцелы (критерий компактности).
- •Ломаные Эйлера и теорема Пеано.
- •Теорема о единственности решения задачи Коши для систем оду. Следствие для оду n-го порядка. Случай линейного уравнения и линейной системы.
- •Лемма о равномерной непрерывности.
- •Непрерывность решения системы оду по начальным данным и параметру.
- •2) , , : & Это следует из открытости множества, непрерывности в точке и условия . Выберем , .
- •Линейная зависимость и независимость вектор-функций. Определитель Вронского.
- •Фундаментальная система решений (фср) для линейной однородной системы оду. Существование фср и их взаимосвязь. Общее решение линейной однородной неоднородной системы.
- •Резольвента линейной системы оду и ее свойства.
- •Построение линейной, однородной системы по известной фср. Формула Лиувилля.
- •Линейные системы с постоянными коэффициентами и методы их решения Случай не нормализуемой системы.
- •Нормальные линейные системы с постоянными коэффициентами и методы их решения
- •Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости.
- •Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант.
- •Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
- •Лемма Адамара.
- •Дифференцируемости решения системы оду по начальным данным и параметру.
- •Первые интегралы систем дифференциальных уравнений. Задание общего решения системы с помощью полной системы первых интегралов.
- •Существование полной системы первых интегралов
- •Линейные однородные УрЧп первого порядка. Связь с первыми интегралами соответствующей системы оду. Замечание о квазилинейных уравнениях.
- •Квазилинейные УрЧп первого порядка. Две леммы о характеристиках.
- •Теорема о существовании единственного решения задачи Коши для квазилинейных УрЧп первого порядка в случае пространственных переменных.
- •По условию 4),
- •Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении.
- •Представление решения краевой задачи для уравнения Штурма-Лиувилля через функцию Грина. Выражение функции Грина и ее свойства.
Лемма Арцелы (критерий компактности).
def:
Семейство
![]() ,
функций
,
функций
![]() называется
равномерно ограниченными,
если
называется
равномерно ограниченными,
если
![]()
![]()
![]()
![]() .
Здесь и в
дальнейшем
.
Здесь и в
дальнейшем
![]() .
.
def:
Семейство
,
функций
называется
равномерно непрерывными,
если
![]()
Пример 1:
Пусть даны числа
![]() и
и
![]() положим
- множество
тех функций
положим
- множество
тех функций
![]() (условие
Гёльдера порядка
(условие
Гёльдера порядка
![]() ),
тогда
равностепенное,
непрерывное семейство. Фиксируем
),
тогда
равностепенное,
непрерывное семейство. Фиксируем
![]() ,
,
![]()
![]() из этого
следует, что можно взять любое
из этого
следует, что можно взять любое
![]() .
Однако,
не является
равномерно ограниченной,
так как
содержит все
константы.
.
Однако,
не является
равномерно ограниченной,
так как
содержит все
константы.
Пример 2:
Возьмем
![]() тогда
− равномерно
ограничено
тогда
− равномерно
ограничено
![]() .
Покажем, что
семейство
не является
равностепенно непрерывным,
то есть выполнено его отрицание
.
Покажем, что
семейство
не является
равностепенно непрерывным,
то есть выполнено его отрицание
![]() .
Положим
.
Положим
![]() .
Пусть
.
Пусть
![]() - произвольное
малое число. Выберем
- произвольное
малое число. Выберем
![]() ,
тогда
,
тогда
![]() больше периода
функции
больше периода
функции
![]() ,
из этого
следует, что на любом интервале длины
,
из этого
следует, что на любом интервале длины
![]() существуют
точки
существуют
точки
![]() и
и
![]() для которых
для которых
![]() ,
а
,
а
![]() .
В этом случае
.
В этом случае
![]() ,
следовательно
не является
равностепенно непрерывным.
,
следовательно
не является
равностепенно непрерывным.
Лемма Арцелы (Arzela – итал.)
Пусть
- равномерно
ограниченное и равномерно непрерывное
семейство функций
,
тогда из каждой
последовательности
![]() можно выделить
последовательность
можно выделить
последовательность
![]() равномерно
сходящейся к непрерывной функции
(
равномерно
сходящейся к непрерывной функции
(![]() может не
принадлежать семейству
).
может не
принадлежать семейству
).
Пример:
![]() тогда
тогда
![]() ,
но
,
но
![]()
Доказательство
◄ Пусть
![]() ,…
– все
рациональные точки на
,…
– все
рациональные точки на
![]() .
Поскольку
.
Поскольку
![]() - ограниченное
множество в
- ограниченное
множество в
![]() (в силу
равномерной ограниченности
),
то существует
подпоследовательность
(в силу
равномерной ограниченности
),
то существует
подпоследовательность
![]() последовательности
последовательности
![]() такая, что
такая, что
![]() фундаментальна
в
(по теореме
Больцано – Вейерштрассе). Поскольку
фундаментальна
в
(по теореме
Больцано – Вейерштрассе). Поскольку
![]() ограничена
в
то существует
подпоследовательность
ограничена
в
то существует
подпоследовательность
![]() последовательности
последовательности
![]() такая, что
такая, что
![]() фундаментальна
в
.
Поскольку
фундаментальна
в
.
Поскольку
![]() ограничена в
то существует
подпоследовательность
ограничена в
то существует
подпоследовательность
![]() последовательности
такая, что
последовательности
такая, что
![]() фундаментальна
в
и так далее.
Получим семейство
последовательностей:
фундаментальна
в
и так далее.
Получим семейство
последовательностей:

Выберем диагональную
подпоследовательность
![]() (метод Кантора).
Покажем, что
искомая
подпоследовательность. Докажем, что
равномерно
фундаментальна на
,
то есть
(метод Кантора).
Покажем, что
искомая
подпоследовательность. Докажем, что
равномерно
фундаментальна на
,
то есть
![]() .
В силу
равностепенной непрерывности семейства
.
В силу
равностепенной непрерывности семейства
![]() .
Разобьем
на равные
отрезки длины меньше
.
Тогда
.
Разобьем
на равные
отрезки длины меньше
.
Тогда
![]() :
в каждом
отрезке этого разбиения есть хотя бы
одна точка из
:
в каждом
отрезке этого разбиения есть хотя бы
одна точка из
![]() (пусть отрезок
разбит на M частей;
для каждой части выбирают
(пусть отрезок
разбит на M частей;
для каждой части выбирают
![]() и выбираем
и выбираем
![]() ).
В силу плотности
рациональных чисел на
.
Заметим
что
).
В силу плотности
рациональных чисел на
.
Заметим
что
![]() – фундаментальна
в
– фундаментальна
в
![]() так как
- подпоследовательность
последовательности
так как
- подпоследовательность
последовательности
![]() ,
начиная с
,
начиная с
![]() .
.
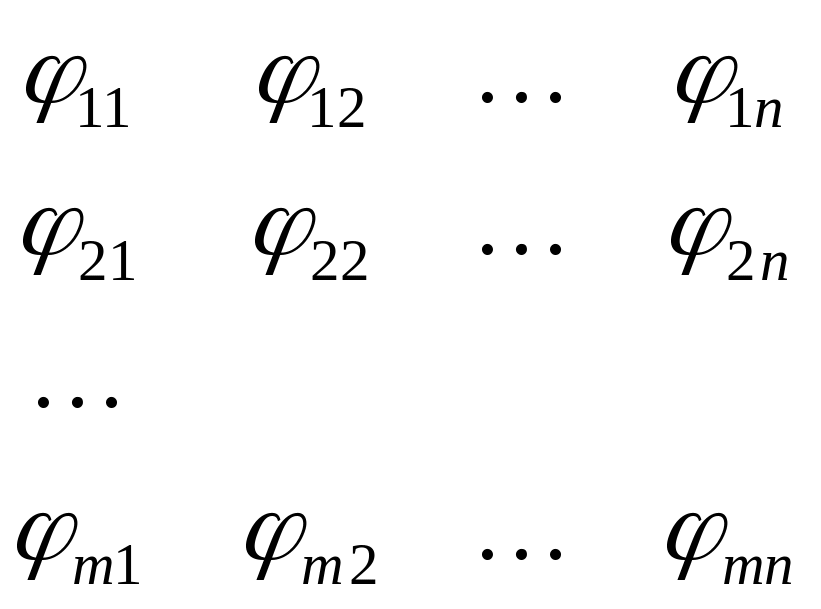
Далее,
![]() ,
,
![]() .
.
Покажем, что это N
– искомое
![]()
![]() .
.
Пусть
![]() ,
,
![]() ,
тогда х
принадлежит
некоторому отрезку
разбиения. В этом отрезке есть хотя бы
одна из точек
,
например
,
тогда х
принадлежит
некоторому отрезку
разбиения. В этом отрезке есть хотя бы
одна из точек
,
например
![]()
![]() (
и
(
и
![]() могут быть на
концах отрезка разбиения). Заметим
могут быть на
концах отрезка разбиения). Заметим
![]() .
.
Имеем
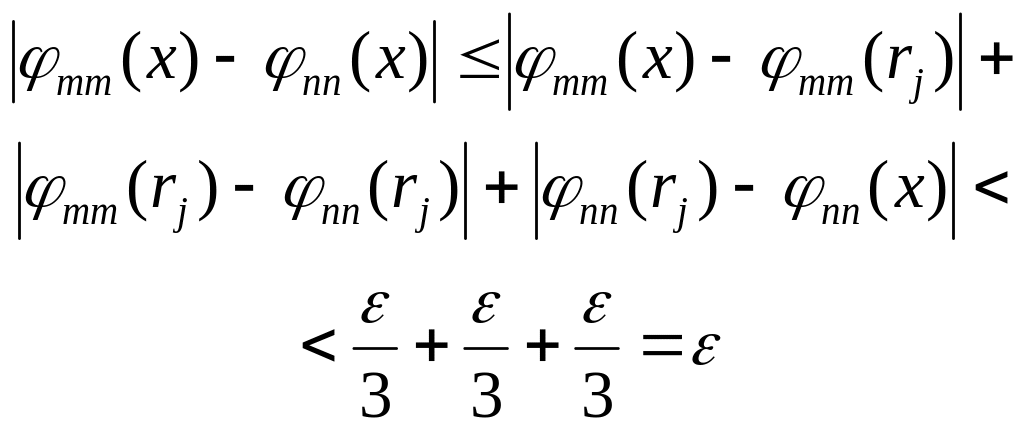 (
(![]() ).
).
Итак,
равномерно
фундаментальна на
.
Поэтому при
каждом фиксированном
последовательность
![]() - фундаментальна
в
и следовательно
по критерию Коши сходится в
к некоторому
элементу
- фундаментальна
в
и следовательно
по критерию Коши сходится в
к некоторому
элементу
![]() .
Устремим в
(
)
m к
.
Устремим в
(
)
m к
![]() .
Получим,
что
.
Получим,
что
![]()
![]() :
:
![]() .
Это означает,
что
сходится
равномерно к
.
Это означает,
что
сходится
равномерно к
![]() на
.
Поскольку
– непрерывна
на
,
то по теореме
из анализа
так же непрерывна
на
.
Лемма доказана
►
на
.
Поскольку
– непрерывна
на
,
то по теореме
из анализа
так же непрерывна
на
.
Лемма доказана
►
