13 Методы решения нелинейных ур-ий (Ньютона, Итераций)

Пусть уравнение имеет единственный корень .

Для того, чтобы использовать метод итерации, необходимо преобразовать уравнение к виду: , где непрерывная на итерационная функция, причем .

Выберем произвольно приближенное значение корня и построим вычислительный процесс:

Продолжая этот процесс неограниченно, получим последовательность приближений к корню. Если существует предел построенной последовательности , то, переходя к пределу в равенстве и предполагая функцию непрерывной, получим равенство: .

Считая, что все приближения принадлежат , имеем закон изменения погрешности в методе итерации:

- представляет коэффициент подавления погрешности за одну итерацию.

На рис. 2.2 видно, что корень уравнения является абсциссой точки пересечения графиков двух функций: и .

Возьмем некоторое начальное приближение , которому отвечает расположенная на кривой точка с координатами (помним, что ). Соединим точку отрезком прямой с лежащей на прямой точкой с координатами . Проведем теперь через точку прямую до пересечения с кривой в точке с координатами . Продолжая этот процесс далее, получаем ломаную линию для которой абсциссы точек представляют собой последовательные приближения к решению .

На рис. 2.3 представлена геометрическая иллюстрация поведения итерационного процесса в четырех простейших случаях взаимного расположения прямой и кривой .

В случаях (а) и (б) метод простой итерации сходится при произвольном начальном приближении. Напротив, в случаях (в) и (г) метод расходится при любом выборе начального приближения. В случаях (а) и (б) (модуль тангенса угла наклона кривой к оси абсцисс меньше единицы), а в случаях (в) и (г) - больше единицы.

Для практического применения необходимо получить простые достаточные условия сходимости метода.

Теорема 2.1: Пусть функция дифференцируема на и для любого выполнены условия:

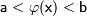1. a < j (x) < b ;

Тогда для любого начального приближения метод итерации сходится к единственному на корню уравнения .

Теорема 2.2: Пусть функция непрерывна на и выполнены условия:

1. - неубывающая на функция;

2. , ;

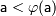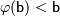3. - единственный на корень уравнения .

Тогда для любого начального приближения метод итерации сходится монотонно к корню уравнения.

Оценка погрешности показывает, что метод простой итерации сходится со скоростью геометрической прогрессии, знаменатель которой равен . Чем меньше , тем выше сокрость сходимости. Видна и роль правильного выбора начального приближения: чем меньше погрешность начального приближения, тем меньше итераций потребуется сделать для достижения заданной точности .

Вычисления следует вести до выполнения неравенства:

Для предварительной оценки количества итераций воспользуемся этой оценкой предельной абсолютной погрешности и получим:

Перейдем к логарифму по основанию и пренебрежем слагаемым , много меньшим в сравнении с . Наименьшее целое , удовлетворяющее неравенству: дает необходимое число итераций.

В этом случае можно считать, что является приближением к с точностью .

для устойчивости метода итерации необходимо, чтобы . Малые значения вычислительной погрешности приводят к незначительным ошибкам в приближении x (i). Метод итерации автоматически исправляет такие ошибки, так как ошибочное значение можно рассматривать как новое начальное приближение x (0), при этом, возможно, возрастет объем вычислений. Свойство самоисправления делает метод итерации одним из важнейших методов вычислений.

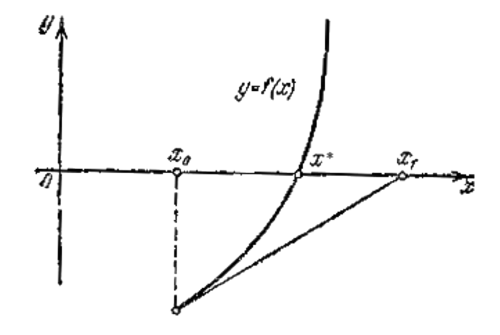
Метод касательных (Метод Ньютона)

Геометрически корнем уравнения является абсцисса точки пересечения графика функции с осью . Пусть – приближенное значение корня. Считая функцию дифференцируемой, построим касательную к графику в точке , рис. 2.4,

и точку пересечения касательной с осью примем за новое приближение

Итак, задавая , приходим к вычислительному процессу, который называется методом Ньютона или методом касательных

По сути метод Ньютона представляет метод итерации в применении к уравнению:

,

Пусть - корень уравнения, тогда погрешность приближения в методе Ньютона с каждой итерацией изменяется следующим образом:

Числитель представляет остаток двучленной формулы Тейлора для функции . Считая ее дважды дифференцируемой, получим:

,

На практике для получения начального приближения, отправляясь от середины промежутка , применяют метод диатомии до получения двух последовательных приближений , , не совпадающих с и и таких, что . За начальное приближение метода Ньютона принимается .

Число необходимых итераций в методе Ньютона зависит только от величины предельной погрешности :

Для практической оценки погрешности применим формулу Лагранжа, получим:

Если получено значение , то приближенное значение корня с погрешностью равно: .