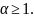- •2) Дифференцируема на интервале (a;b) ;
- •1) Непрерывна на отрезке [a;b];
- •2) Дифференцируема на интервале (a;b).
- •2. Признаки монотонности ф-ии
- •3.Необходимые и достаточные условия экстремума функции
- •4. Выпуклость и вогнутость графика функции. Точка перегиба
- •5. Асимптоты графика функции
- •6. Касательная и нормаль к плоской кривой
- •8. Частные производные и полный дифференциал
- •10. Первообразная. Неопределенный интеграл
- •11. Таблица интегралов
- •12. Общие методы интегрирования
- •13.Интегрирование простейших рациональных дробей
- •14. Разложение рациональных дробей на сумму элементарных дробей
- •15. Интегрирование простейших иррациональных выражений
- •16. Определение определенного интеграла
- •17. Основные свойства определенного интеграла(с док-вом)
- •18. Определенный интеграл с переменным пределом интегрирования. Теорема Барроу(док-во)
- •19Ньютона-Лейбница(док-во)
- •20. Методы вычисления определенного интеграла
- •21. Вычисление площадей с помощью определенного интеграла(в прямоугольной и полярной системе координат)
- •24. Интеграл с бесконечными пределами и от неограниченной ф-ии
- •25. Понятие о диф уравнении. Основные поянтия(решение, общее решение, задача Коши)
- •26. Диф уравнение с разделяющимися переменными. Однородные диф уравнения
- •37. Признак Лейбница
- •41. Разложение элементарных функций в степенной ряд Тейлора и Маклорена
18. Определенный интеграл с переменным пределом интегрирования. Теорема Барроу(док-во)
Пусть функция f(t)
определена и непрерывна на некотором
промежутке, содержащем точку a.
Тогда каждому
числу x из
этого промежутка можно поставить в
соответствие число
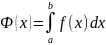 ,
определив тем самым на промежутке
функцию Ф(x),
которая называется определенным
интегралом с переменным
,
определив тем самым на промежутке
функцию Ф(x),
которая называется определенным
интегралом с переменным
верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x.
♦Для этого сначала рассмотрим приращение функции в точке x при приращении аргумента Δx.
ΔФ(x)
= Ф(x + Δx)
– Ф(x)
=
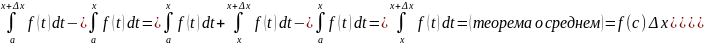 ,
с
,
с
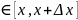 Отсюда
следует формула для производной функции
Ф(x):
Отсюда
следует формула для производной функции
Ф(x):
 ♦
♦
Теорема (теорема
Барроу). Если f (x) непрерывна на [a,b], то
функция Φ(x) является дифференцируемой
на [a,b], причем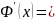 .
.
Эта теорема
доказывает, что любая функция f (x)
непрерывная на [a,b], имеет первообразную.
Именно,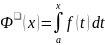 является одной из первообразных.
является одной из первообразных.
19Ньютона-Лейбница(док-во)
Т: Если
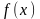 непрерывна на
непрерывна на

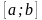 , справедлива ф-ла Ньютона-Лейбница:
, справедлива ф-ла Ньютона-Лейбница:
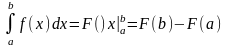
ВЫВОД ФОРМУЛЫ:
Рассм-м
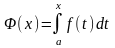 , т.к.
, т.к.
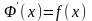 ,
то
,
то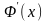 -
первообразная для
.
Но
-
первообразная для
.
Но
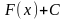 ,
также первообразная. Это значит что
имеет место следующее равенство :
,
также первообразная. Это значит что
имеет место следующее равенство :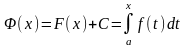
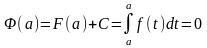
Подставим верхнюю границу:
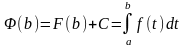
 подставами
вместо
подставами
вместо
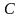 :
:
 в силу 1-го
свойства, что значении определенного
интеграла независит от обозначения
переменной интегрирования, запишем:
в силу 1-го
свойства, что значении определенного
интеграла независит от обозначения
переменной интегрирования, запишем:
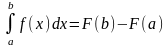
20. Методы вычисления определенного интеграла
Замена переменной
и интегрирование по частям в определенном
интеграле. МЕТОД
ПОДСТАНОВКИ.
 Выберем х=
Выберем х= , которая дифференцируема на [
, которая дифференцируема на [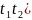 . Если х=
. Если х= и х=
и х= ,
то исх интеграл
,
то исх интеграл
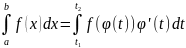 .
Отличие метода подстановки для
определенного интеграла – нет возврата!
.
Отличие метода подстановки для
определенного интеграла – нет возврата!
ПО ЧАСТЯМ: Пусть
заданы u=u(x),
v=v(x)
, диф-емые на [a,b].
Тогда
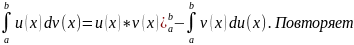 ф-лу инт-ия по частям для неопр интеграла.
ф-лу инт-ия по частям для неопр интеграла.
21. Вычисление площадей с помощью определенного интеграла(в прямоугольной и полярной системе координат)
ПЛОЩАДИ
ПОВ-ТЕЙ ТЕЛ ВРАЩЕНИЯ: 1)
y=f(x)
непрерывна на отрезке [a,b
] – в случае вращения графика этой ф-ии:
S=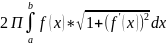 ; 2) В случае параметрического задания
дуг кривой: x=x(t),
y=y(t),
t[t1,t2]
; 2) В случае параметрического задания
дуг кривой: x=x(t),
y=y(t),
t[t1,t2]
S=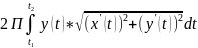 ; 3) В случае задания дуги кривой уравнением
r=r(
; 3) В случае задания дуги кривой уравнением
r=r(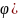 в полярных координатах
в полярных координатах
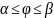
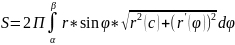 .
.
22.
ОБЪЕМ
ТЕЛА ВРАЩЕНИЯ : Пусть
функция y=f(x)
непрерывна на отрезке [a,b
]. В этом случае объем тела, образованного
вращением около оси 0x
криволинейной трапеции, ограниченной
графиком функции y=f(x),
прямыми x=a
, x=b
и осью абсцисс , может быть найден по
формуле:
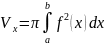 . Если вращение происходит вокруг оси
0у, то объем тела вращения находится по
формуле:
. Если вращение происходит вокруг оси
0у, то объем тела вращения находится по
формуле:
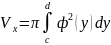
23.
ДЛИНА
ДУГИ:
Под длиной дуги понимается предел, к
которому стремится длина ломаной линии,
вписанной в эту дугу, при условии, что
количество звеньев ломаной линии
неограниченно возрастает, и при этом
длина наибольшего звена ломаной стремится
к нулю. Если дуга задана непрерывно
дифференцируемой функцией y=f(x) , то ее
длина l вычисляется по формуле :
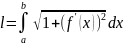
24. Интеграл с бесконечными пределами и от неограниченной ф-ии
Интегралы с бесконечными пределами интегрирования и интегралы от неограниченных ф-ций газ несобственными интегралами.
Пусть
ф-я
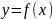 непрерывна на промежутке
непрерывна на промежутке
 и интегрируема на любом конечном его
отрезке
и интегрируема на любом конечном его
отрезке
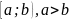 .
Тогда несобственным интегралом с
бесконечным верхним пределом наз предел
.
Тогда несобственным интегралом с
бесконечным верхним пределом наз предел
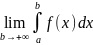 ,
к-й обознач символом
,
к-й обознач символом
 ,
т.е.
,
т.е.
 Если
предел сущ и конечен, то несобственный
интеграл наз сходящимся, в противном
случае – расходящимся.
Если
предел сущ и конечен, то несобственный
интеграл наз сходящимся, в противном
случае – расходящимся.
Аналогично
опред несобств интегралы на промежутке
и
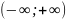 :
:
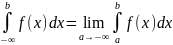
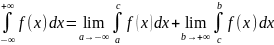
Если
сходятся оба интеграла в правой части
последней формулы, то интеграл
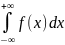 наз сходящимся, и расходящимся, если
хотя бы 1 из них расходится. Если f(x)
непрерывна
для всех х
отрезка [a,b],
кроме точки с,
в к-й f(x)имеет
разрыв II рода, то по определению имеет
разрыв II рода, то по определению
наз сходящимся, и расходящимся, если
хотя бы 1 из них расходится. Если f(x)
непрерывна
для всех х
отрезка [a,b],
кроме точки с,
в к-й f(x)имеет
разрыв II рода, то по определению имеет
разрыв II рода, то по определению
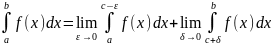 ,
где
,
где
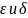 изменяются независимо друг от друга.
изменяются независимо друг от друга.
Несобственный
интеграл
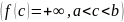 наз сходящимся, если оба предела в правой
части равенства существуют, и расходящимся,
если не существует хотя бы 1 из них.
наз сходящимся, если оба предела в правой
части равенства существуют, и расходящимся,
если не существует хотя бы 1 из них.
В
случае с=а
или
c=b
получаем

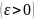 ,
или
,
или
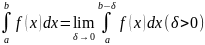 . При исследовании сходимости несобств
инт-ов пользуются одним из признаков
сравнения. 1) Если ф-ии f(x)
и
. При исследовании сходимости несобств
инт-ов пользуются одним из признаков
сравнения. 1) Если ф-ии f(x)
и
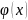 определены на промежутке [a;
+
определены на промежутке [a;
+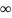 ),
интегрируемы на отрезке [a,A],
где A
),
интегрируемы на отрезке [a,A],
где A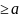 и 0
и 0 для всех x
,
то из сходимости интеграла
для всех x
,
то из сходимости интеграла
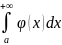 следует сх-ть интеграла
следует сх-ть интеграла
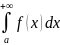 ,
а из расходимости интеграла
вытекает расх-ть инт-ла
.
(признак сравнения). 2) Пусть на
промежутке [a;
+
)
определены 2 положительные функции f(x)
и
,
инт-емые на любом конечном промежутке
[a,b].
Тогда , если существует конечный предел
,
а из расходимости интеграла
вытекает расх-ть инт-ла
.
(признак сравнения). 2) Пусть на
промежутке [a;
+
)
определены 2 положительные функции f(x)
и
,
инт-емые на любом конечном промежутке
[a,b].
Тогда , если существует конечный предел
 то
интегралы
и
сходятся и расх-ся одновременно
(предельный признак сравнения).
3)Если интеграл
то
интегралы
и
сходятся и расх-ся одновременно
(предельный признак сравнения).
3)Если интеграл
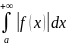 сходится, то сходится и инт-л
.
В этом случае инт-л
называется абсолютно сходящимся. 4)
Если при x
-> +
ф-я f(x)>0
является бесконечно малой порядка
сходится, то сходится и инт-л
.
В этом случае инт-л
называется абсолютно сходящимся. 4)
Если при x
-> +
ф-я f(x)>0
является бесконечно малой порядка
 по сравнению с
по сравнению с
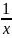 ,
то интеграл
сходится при
,
то интеграл
сходится при
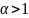 и расходится при
и расходится при
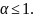 На практике часто для сравнения
используется ф-ия
На практике часто для сравнения
используется ф-ия
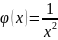 .
Известно, что
.
Известно, что
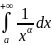 сходится при
и расх-ся при
Аналогичные признаки сх-ти можно указать
и для инт-ов от разрывных ф-ий. Для
сравнения в признаке 4) используют инт-л
сходится при
и расх-ся при
Аналогичные признаки сх-ти можно указать
и для инт-ов от разрывных ф-ий. Для
сравнения в признаке 4) используют инт-л
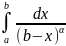 (
(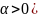 или
или
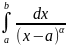 ,
который сходится при
,
который сходится при
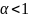 и расх-ся при
и расх-ся при