Главные оси и моменты инерции. Радиусы инерции.
Оси, относительно которых центробежный
момент инерции равен нулю называются
главными. Если начало координат совпадает
с центром тяжести сечения, то они
называются главными центральными осями.
Моменты инерции относительно этих осей
называются главными. Формула для
определения главных осей:
.Для
квадрата и круга все центральные оси
– главные. Осевые моменты инерции
относительно главных осей принимают
свои максимальные значения.
Радиусом инерции сечения относительно
некоторой оси, называется величина,
определяемая по формуле:
( радиус инерции равен расстоянию от
оси х, до той точки, в которой следует
условно сосредоточить площадь сечения
F, чтобы момент инерции
этой точки был равен моменту инерции
всего сечения. Главными радиусами
инерции являются соответственно корень
из отношения максимального или
минимального момента инерции к площади.
Понятие о чистом сдвиге. Закон Гука при сдвиге.
Кроме деформации растяжения или сжатия материал нагруженного элемента конструкции может испытывать деформацию сдвига. γ – угол сдвига. Напряжённо-деформированное состояние, характеризуемое тем, что на гранях элемента возникают только касательные напряжения, называют чистым сдвигом.
Закон Гука при сдвиге. До предела
пропорциональности при сдвиге, что на
диаграмме сдвига соответствует точке
перехода графика к криволинейному
участку, справедлива линейная зависимость:
,
которая носит название закона Г. при
сдвиге. G- это модуль
упругости материала при сдвиге:
,
измеряется в Па’скалях. Потенциальная
энергия при чистом сдвиге для объема
V:
,
где величина u - плотность
энергии деформации или удельной
потенциальной энергией деформации при
чистом сдвиге:
Определение напряжений при кручении стержней круглого поперечного сечения.
Н
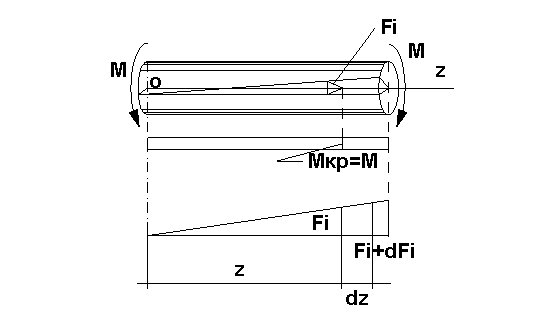а
рисунке общая деформация кручения
стержня с круглым сечением. Эта деформация
характерна тем, что поперечные сечения
поворачиваются вокруг оси стержня z
на углы φ=φ(z), называемые
углами закручивания, а в поперечных
сечениях возникают касательные напряжения
τ, приводящееся к крутящему моменту Mz
(если он направлен по ходу часовой
стрелки, то он положителен). Вывод формулы
касательных напряжений. Допущения:
гипотеза плоских сечений (при кручении
поперечные сечения остаются плоскими),
все радиусы данного сечения остаются
прямыми и поворачиваются на один и тот
же угол φ – т.е каждое сечение поворачивается
вокруг оси как тонкий плоский диск.
Согласно допущением, кручение представляет
собой деформацию сдвига материала,
заключённого между соседними поперечными
сечениями, вызванную относительным
поворотом этих осей вокруг оси z.
С использованием указанных допущений
на рисунке изображена деформация
элемента стержня dz
(произвольно выбранного). Точка К при
кручении переместиться в точку К1, тогда
дуга КК1 =pdφ=γdz,
по закону Гука получим касательное
напряжение:
Где G, и dfi/dz = const для всех точек сечения, и следовательно касательное напряжение изменяется пропорционально р.
Во всех точках окружности радиуса р напряжение изменяется равномерно (const), и направлено по касательной к этой окружности.
В
еличина
является относительным углом закручивания
и имеет размерность рад/м. Из условия,
что напряжения сводятся к крутящему
моменту Mz, получаем:
,
где произведение GJp –
жёсткость при сечения при кручении.
.
При расчётах на прочность, используется формула
,
здесь
