Обобщённый закон Гука при трёхосном напряжённом состоянии. Физический смысл величин, входящих в закон Гука.

Зависимости в общем случае нагружения. На гранях выделенного элемента возникают нормальные и касательные напряжения. Касательные напряжения, вызывая деформации сдвига, не вызывают изменения длин сторон элемента, (рис без касательных напр.) т.е линейные и угловые деформации можно рассматривать как независимые. (справедливо только для изотропного материла в случае линейных зависимостей между напряжениями и деформациями) Используем принцип суперпозиции и рассмотрим линейные деформации относительно оси x, обусловленные нормальными напряжениями.(на рис сигмы- во все стороны) от действия только напряжения сигм_х, деформация в направлении оси х равна:

,складывая деформации ,вызванные напряжениями сигм_у и сигм_z, окончательно получим:

рассуждая аналогично можно получить деформации относительно других осей:

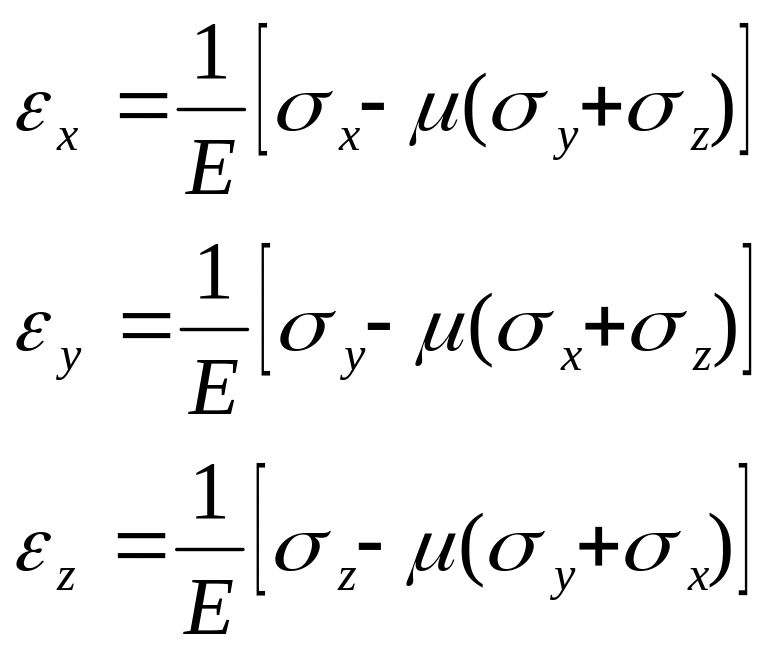Формулы обобщённого закона Гука

полные напряжения на наклонной площадке равны. P_alpha=sigm*cos(alpha)

Расчёты на прочность. Метод предельных состояний и метод допускаемых напряжений. Проверка прочности и подбор сечений при центральном растяжении и сжатии.

Предельным считается состояние, когда конструкция перестаёт удовлетворять эксплуатационным требованиям. Различают две группы предельных состояний

1. Непригодность к эксплуатации по причинам потери несущей способности

2. Непригодность к эксплуатации в соответствии с техническими или бытовыми требованиями

Нормативное значение нагрузки и воздействий соответствует их значению при нормальной эксплуатации. Они устанавливаются СНиП-ом. Возможное отклонение значений нагрузки от нормативных значений учитывается коэффициентом надёжности по нагрузке n<>1.

Нагрузки и воздействия, помноженные на коэффициент называются расчётными. Нормативное сопротивление, предел текучести и временного сопротивления также задаются по нормам. Возможное отклонение в неблагоприятную сторону от значений нормативного сопротивления учитывается коэффициентом надёжности по материалу γм>1. Этот коэффициент отображает статическую изменяемость свойств материала.

Расчётное сопротивление . Особенности действительной работы материалов, элементов конструкций, их соединений, учитывается коэффициентом условий работы γ. В большинстве случаев при нормальных условиях работы он равен 1. Степень ответственности и капитальности сооружений а также значимость последствий тех или иных предельных состояний учитывается коэффициентом надёжности по назначению γн.Надёжность и гарантия от возникновения предельных состояний первой группы, обеспечиваются выполнением следующего условия: N<=S, где S – предельное усилие, которое может воспринять рассчитываемый элемент. N=n*Pн, S=FнтRнγ/(γнγм)=FRγ/γн, при центрально растянутом/сжатом элементе (γн=1) условие прочности примет вид:

Метод допускаемых напряжений. (при расчёте машиностроительных деталей и механических узлов)

Осовой метода является предположение, что критерием надёжности конструкции будет выполнение следующего условия прочности:

, где сигм_макс –наибольшее рабочее напряжение в одной из точек опасного сечения и определяемого расчётом, [сигм] допускаемое (предельное) напряжение для данного материала, полученное путём экспериментальных исследований: (опасное напряжение делённое на коэффициент запаса прочности). Для пластичных материалов за опасное напряжение принимается предел текучести, а для хрупких – временное сопротивление (предел прочности). n – зависит от многих факторов (для сооружений и машин 1,4…1,6; для хрупких материалов 2,5…3,5; для древесины 3,5…6)

Главные площадки и главные напряжения. Три вида напряжённого состояния. Наибольшие касательные напряжения. Двухосное напряжённое состояние (см ранее). Напряжения на наклонных площадках. Главные площадки и главные напряжения.

Рассмотрим стержень, растянутый равномерно распределённой нагрузкой. Определим напряжения на наклонной площадке, составляющей угол α с поперечным сечением. (рис) Рассечём стержень по этому наклонному сечению и отбросим правую его часть. На наклонной площадке полные напряжения будут направлены вдоль продольной оси и распределены равномерно. Оставшаяся левая часть должна находиться в равновесии. Поэтому равнодействующие вешней нагрузки сигма и полных напряжений должны быть равными между собой: , где F_alpha= F/cos(alpha) – площадь наклонного сечения. Таким образом площадь наклонного сечения: . Разложим полное напряжение.

На площадках, совпадающих с поперечным сечением, т.е. при альфа=0

На площадках, наклонённых под углом 45град:

На продольных площадках оба напряжения равны 0.