
- •1. Криволинейный интеграл I рода. Основные свойства. Вычисление криволинейного интеграла I рода.
- •2. Криволинейный интеграл II рода. Его вычисление. Связь между криволинейными интегралами I и II рода.
- •3. Формула Грина.
- •4. Поток, ф-ла Гаусса-Остроградского.
- •5. Инвариантное определение дивергенции, соленоидальные поля.
- •6. Линейный интеграл. Ф-ла Стокса.
- •7. Инвариантное определение ротора.
- •8. Необх. И достаточные условия независимости линейного интеграла от пути интегрирования.
- •9. Закон Архимеда
- •15 Повторение испытаний. Схема Бернулли и полиномиальная.
- •29 Метод моментов
5. Инвариантное определение дивергенции, соленоидальные поля.
Рассмотрим
произвольную точку M
в пространственной области V.
Выберем ее окрестность VM
– шар радиуса r
с центром в точке M.
Обозначим
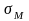 - ее границу – сферу радиуса r.
По теореме о среднем для тройного
интеграла
- ее границу – сферу радиуса r.
По теореме о среднем для тройного
интеграла
 (по формуле Остроградского – Гаусса).
Стягиваем окрестность к точке M,
получаем дивергенцию векторного поля
в точке M.
(по формуле Остроградского – Гаусса).
Стягиваем окрестность к точке M,
получаем дивергенцию векторного поля
в точке M.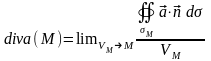 .
Это и есть инвариантное
определение дивергенции.
Поэтому
дивергенция векторного поля в точке M
имеет смысл объемной плотности потока
векторного поля через окрестность этой
точки и характеризует мощность источника
(если
.
Это и есть инвариантное
определение дивергенции.
Поэтому
дивергенция векторного поля в точке M
имеет смысл объемной плотности потока
векторного поля через окрестность этой
точки и характеризует мощность источника
(если
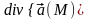 >0)
или стока (если
<0)
векторного поля в точке M.
Если
>0,
то точка M
– источник векторного поля, если
<0,
то точка M
– сток векторного поля. Если в некоторой
области дивергенция равна нулю, то в
этой области нет ни источников, ни
стоков, поток векторного поля через
границу такой области равен нулю –
«сколько поля втекает в область, столько
и вытекает из нее». Пример.
Определить расположение источников и
стоков векторного поля
>0)
или стока (если
<0)
векторного поля в точке M.
Если
>0,
то точка M
– источник векторного поля, если
<0,
то точка M
– сток векторного поля. Если в некоторой
области дивергенция равна нулю, то в
этой области нет ни источников, ни
стоков, поток векторного поля через
границу такой области равен нулю –
«сколько поля втекает в область, столько
и вытекает из нее». Пример.
Определить расположение источников и
стоков векторного поля
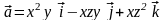 .
Выяснить, является ли точка M(1,2,3)
источником или стоком.
.
Выяснить, является ли точка M(1,2,3)
источником или стоком.
 .
Все точки, для которых 2xy+xz
>0 – источники, все точки, для которых
2xy+xz
<0 – стоки. На поверхности 2xy+xz
= 0 нет ни источников, ни стоков. Точка
M
– источник, так как
.
Все точки, для которых 2xy+xz
>0 – источники, все точки, для которых
2xy+xz
<0 – стоки. На поверхности 2xy+xz
= 0 нет ни источников, ни стоков. Точка
M
– источник, так как
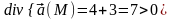 .
.
Свойства
1) Линейность: для любых векторных полей
F
и G
и для всех вещественных чисел a
и b
![]()
2)
Если φ — скалярное поле, а F —
векторное, тогда:![]() или
или
![]()
3)
Свойство, связывающее векторные поля
F
и G,
заданные в трёхмерном пространстве, с
ротором:![]() или
или![]() 4)
Дивергенция от градиента есть лапласиан:
4)
Дивергенция от градиента есть лапласиан:![]() 5) Дивергенция от ротора:
5) Дивергенция от ротора:![]()
Соленоидальное
поле и его свойства.Векторное
поле
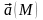 называется
соленоидальным
в области V,
если в любой точке M
этой области
называется
соленоидальным
в области V,
если в любой точке M
этой области

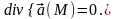
Свойства 1) Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю. 2) Необходимость следует из формулы Остроградского – Гаусса, достаточность – из инвариантного определения дивергенции. 3) Поток соленоидального поля через любую поверхность, окружающую изолированный источник или сток, один и тот же. 4) Поток соленоидального поля через произвольное сечение векторной трубки один и тот же.
Следствие. Векторные линии соленоидального поля не могут начинаться и заканчиваться внутри поля. В самом деле, иначе конечный поток приходился бы на нулевую площадь источника или стока, что требовало бы бесконечной мощности источника или стока.
6. Линейный интеграл. Ф-ла Стокса.
Линейным
интегралом векторного поля
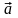 по дуге L
называется криволинейный интеграл
по дуге L
называется криволинейный интеграл
 .
Линейный интеграл имеет смысл работы
векторного поля при перемещении по
дуге. Циркуляцией векторного поля
называется линейный интеграл по
замкнутому контуру.
.
Линейный интеграл имеет смысл работы
векторного поля при перемещении по
дуге. Циркуляцией векторного поля
называется линейный интеграл по
замкнутому контуру.
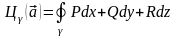 .
Вводя эти понятия, можно записать формулу
Стокса в «полевой» форме.
.
Вводя эти понятия, можно записать формулу
Стокса в «полевой» форме.
 .
Мы определили ротор векторного поля в
декартовой системе координат, однако
ротор – это характеристика самого
векторного поля Поэтому необходимо
дать определение ротора, которое не
зависит от выбора системы координат.
Пусть
поверхность S
ограничена кусочно-гладким контуром
L.
Пусть функции: P(x,y,z),
Q(x,y,z),
R(x,y,z)
– непрерывно дифференцируемы на
поверхности S.
Тогда имеет место
формула Стокса:
.
Мы определили ротор векторного поля в
декартовой системе координат, однако
ротор – это характеристика самого
векторного поля Поэтому необходимо
дать определение ротора, которое не
зависит от выбора системы координат.
Пусть
поверхность S
ограничена кусочно-гладким контуром
L.
Пусть функции: P(x,y,z),
Q(x,y,z),
R(x,y,z)
– непрерывно дифференцируемы на
поверхности S.
Тогда имеет место
формула Стокса:
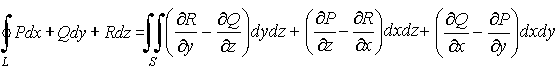 т. е. формула Стокса устанавливает связь
между интегралом по поверхности и
криволинейным интегралом по контуру,
ограничивающему эту поверхность.
т. е. формула Стокса устанавливает связь
между интегралом по поверхности и
криволинейным интегралом по контуру,
ограничивающему эту поверхность.
