Ферримагнетики.

Ферримагнетики (оксидные ферримагнетики называют ферритами) также имеют две магнитных подрешетки с противоположно направленными спинами, которые, однако, в отличие от антиферромагнетиков, скоменсированы неполностью. Наиболее исследованы и нашли широкое применение ферриты, например, MeO*Fe₂O₃, где Me=(Mg²⁺, Zn²⁺, Cu²⁺, Ni²⁺, Fe²⁺, Mn²⁺) или Ме²⁺[Fe²⁺Fe³⁺]O₄, имеющие кубическую структуру типа шпинель или гранат. В элементарной ячейке магнетита, Fе²⁺[Fe²⁺Fe³⁺]O₄, (рис.5.2), 8 ионов Fe³⁺, занимающие тетраэдрические положения, и 8 ионов Fe³⁺, занимающие октаэдрические положения имеют противоположную ориентацию спинов и поэтому их моменты компенсируются. Магнетизм обусловлен 8-ью электронами Fe²⁺, занимающими тетраэдрические положения, как схематично показано ниже:

Рис. 5.2 . Ферримагнитное упорядочение в магнетите Fе²⁺[Fe²⁺Fe³⁺]O₄.

S=5/2 ... ... S=2 октаэдрические положения

8Fe³⁺ 8Fe²⁺

... тетраэдрические положения

8Fe³⁺

Магнитные свойства некоторых ферримагнетиков приведены в таблице 5.2.

Таблица 5.2. Ферримагнетики.

Вещество	Намагниченность Ms (Гс)		n(0K)=μ/μB	TC, K
	Т = 300 К	Т= 0К
MnAs	670	870	3.4	318
MnBi	620	680	3.52	630
MnSb	710	-	3.5	587
CrO2	515	-	2.03	386
MnOFe2O3	410	-	5.0	573
FeOFe2O3	480	-	4.1	585
NiOFe2O3	270	-	2.4	858
CuOFe2O3	135	-	1.3	728
MgOFe2O3	110	-	1.1	713
EuO	-	1920	6.8	69
Y3Fe5O12	130	200	5.0	560

Значительную часть ферримагнетиков составляют диэлектрические и полупроводниковые ионные кристаллы, содержащие магнитные ионы различных элементов и одного элемента, но находящихся в разных кристаллографических позициях (в неэквивалентных узлах кристаллографической решетки).

Условие ферримагнетизма.

Представим себе кристалл, имеющий две магнитных подрешетки А и В с антипараллельными () магнитными моментами. В этом случае:

B_A=-M_A-M_B; B_В=- M_A-M_B, ,,>0. (5.1)

U= -1/2(B_AM_A+B_BM_B)=1/2M_A²+ M_A M_B+1/2M_B² . (5.2)

Энергия ниже, когда M_AM_B. Энергия  0, когда M_A=M_B=0. -ное состояние устойчиво, когда

M_AM_B>1/2(M_A²+M_B²). (5.3)

Температура Нееля, Кюри-Вейса и восприимчивость ферримагнетиков.

Определим константы Кюри C_A и C_B для подрешеток А и В. Для простоты пренебрежем всеми взаимодействиями, кроме -ного между А- и В- подрешетками: B_A=-M_B; B_B=-M_A;

В приближении среднего поля

M_AT=C_A(B_a-M_B); M_BT=C_B(B_a-M_A). (5.4)

При B_a =0 эта система уравнений становится однородной относительно M_A и M_B и имеет решение, если

=0. (5.5)

Отсюда ферромагнитная температура Кюри дается выражением

T_c=(C_AC_B)^1/2. (5.6)

Решая (5.4), мы получим восприимчивость при T>T_с

=(M_A+M_B)/B_A=((C_A+C_B)T-2C_AC_B)/(T²-T_c²) . (5.7)

При C_A=C_B =C – антиферромагнетизм.

Антиферромагнетик – это скомпенсированный ферримагнетик. Пример: MnO (рис.5.1), где спины Mn²⁺ скомпенсированы. Переход из антиферромагнитной фазы в парамагнитную происходит при температуре Нееля, Т_N:

T_N=C, =(2CT-2C²)/(T²-(C)²), т.е. =2C/(T+T_N) при T>T_N. (5.8а)

В действительности экспериментальные значения укладываются в зависимость

=C/(T+) при T>T_N. (5.8б)

Температуру  называют температурой Кюри-Вейса. Отношение /T_N ~ 1  5 и часто отличается от 1 (см. также таблицу 5.2). Качественное сопоставление хода температурных зависимостей магнитных восприимчивостей для парамагнетиков, ферромагнетиков и антиферромагнетиков приведено на рис.5.3.

Восприимчивость антиферромагнетиков ниже температуры Нееля.

Рассмотрим два случая, когда внешнее поле перпендикулярно и параллельно полному спину: 1) B_aS и 2) B_aS.

Рис. 5.3. Температурная зависимость магнитной восприимчивости парамагнетиков, ферромагнетиков, антиферромагнетиков.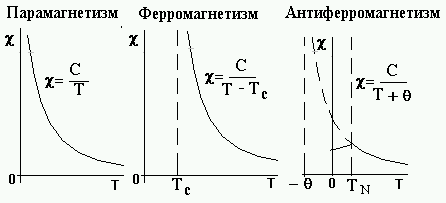

При T>T_N const (т.е. практически не зависит от взаимной

ориентации поля и спинов - парамагнитное поведение).

П

Рис. 5.4. Температурная зависимость магнитной восприимчивости для антиферромагнетиков при перпедикулярной (_) и параллельной (_) ориентации B_a.

ри T<T_N, если B_aS, то можно считать, что в этом случае плотность энергии при |M_A| = |M_B| = M, то

-2U=M_AB_A+M_BB_B,

B_A= B_a-M_B B_B= B_a-M_A. Тогда -2U=M_A B_a- M_A M_B+ M_BB_a- M_B M_A. Т.е. -2U=B_a(M_A+ M_B)-2 M_A M_B, или

U = M_AM_B -1/2B_a(M_A+M_B)  M²[1-1/2(2)²]-2B_aM/2, (5.9)

где 2 -угол между S_A и S_B. Минимум энергии будет при dU/d=0=4M² - B_aM

или в устойчивом состоянии =B_a/4M. (5.10)

Т.о. _=2M/B_a=1/2. (5.11)

В ||-ной ориентации M_ = M_A + M_B = 0 при Т = 0, поэтому восприимчивость при T=0K равна нулю _(0)=0. Эксперимен-тальная зависимость _ и _ для MnF₂ показана на рис. 5.4.