Операторы простой структуры
Линейный оператор
называется оператором простой структуры,
если он имеет n
линейно независимых собственных
векторов. Он так называется потому, что
в базисе из собственных векторов матрица
этого оператора имеет диагональный
вид. Действительно: пусть
– линейно независимые собственные
векторы оператора A.
Они образуют базис в пространстве
.
Построим матрицу оператора в этом
базисе:
.
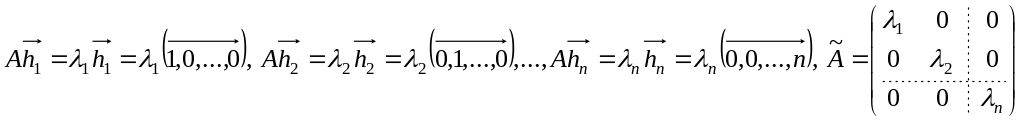Если в каком-либо базисе
матрица оператора имеет диагональный
вид
,
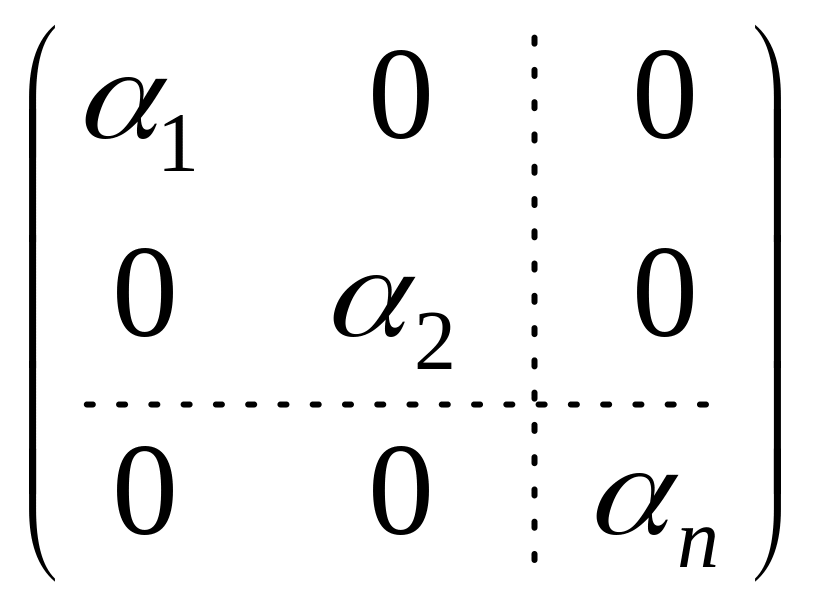где не все
различные, то векторы базиса являются
собственными для оператора A.
Если
– различные собственные числа оператора
(т.е.
для
),
то соответствующие им собственные
векторы образуют линейно независимую
систему.
Пусть
– собственное число,
– собственный вектор. Тогда
и
– линейно независимая система,
следовательно, для k
= 1 теорема верна. Пусть теперь теорема
верна для k – 1
собственного числа. Докажем тогда, что
только при
,
т.е. векторы
– линейно независимые. Подействуем на
обе части этого уравнения оператором
,
что равносильно
.
Домножим первое уравнение на
.
Вычтем из предпоследнего уравнения
последнее:
.
В силу линейной независимости
можно утверждать, что это равенство
выполняется только при
,
а т.к.
при k
i по условию и
,
т.к. это собственные числа, то
.
Тогда
,
т.к. линейно независимы.
Если линейный оператор имеет n собственных чисел, то он – оператор простой структуры.
Инвариантные подпространства
Подпространство
называется инвариантным относительно
оператора A,
если для
будет
.
Пусть
– собственные векторы оператора
.
Тогда линейная оболочка этих векторов
является инвариантным подпространством
относительно оператора A.
Евклидово пространство
Линейное пространство
называется евклидовым, если в нём задано
правило, по которому каждым двум векторам
из
ставится в соответствие число. Обозначение:
.
Причём для этого правила должны
выполняться три условия:
.
.
.
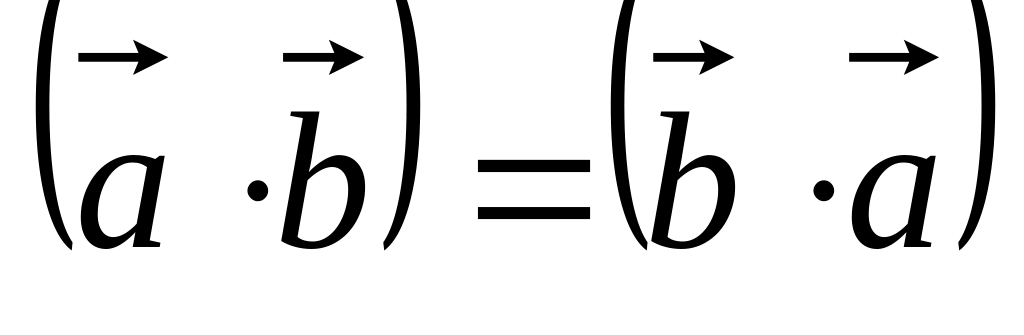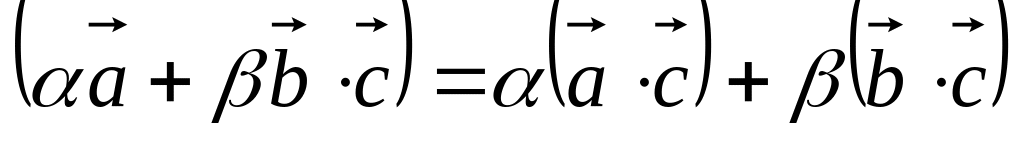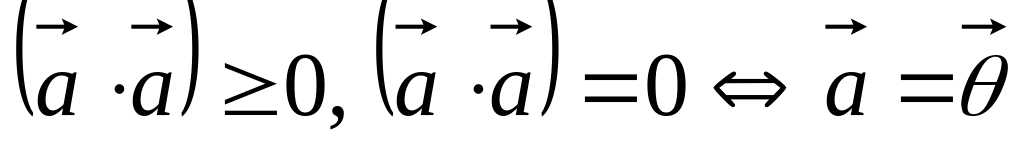Это число называется
скалярным произведением, а евклидово
пространство размерности n
обозначается
.
Пример: {
интегрируемы на
}.
Тогда
.
Ортогональные векторы
Два вектора
и
называются ортогональными, если
.
Если в предыдущем примере
,
то sin x
и cos x ортогональны.
Нормой элемента
называют число
.
Для нашего примера
.
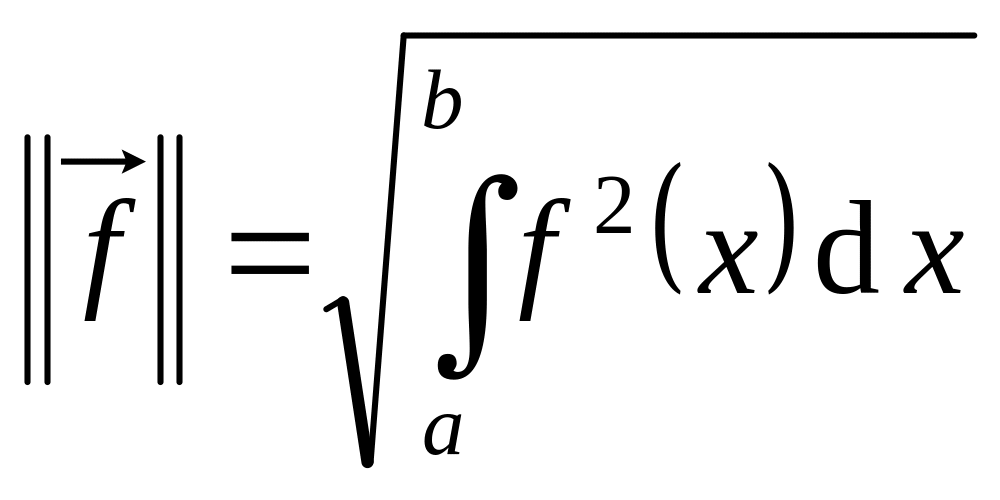Теорема Пифагора: Если
,
то
.
,
т.к.
.
Неравенство Коши-Буняковского:
.
Рассмотрим
для
.
Неравенство треугольника:
.
.
Угол между векторами
Углом между векторами
и
называют число
.
Система векторов называется ортогональной, если векторы этой системы попарно ортогональны.
Ортогональная система ненулевых векторов является линейно независимой.
Пусть
– ортогональная система векторов и
пусть
,
где
– числа. Умножим обе части этого равенства
на
.
Тогда
или
.
Аналогично для
– линейно независимая система.
Ортогональная система векторов называется ортонормированной, если нормы всех векторов равны единице.
Базис в евклидовом пространстве называется ортонормированным, если он составлен из ортонормированной системы векторов.