Ядро, образ, ранг, дефект.

Ядром оператора A называется множество векторов пространства , которые отображают этот оператор в . Обозначение: .

Образом оператора A называют .

Ядро и образ линейного оператора являются линейными подпространствами.

Пусть . Это означает, что . Но тогда . Для образа аналогично.

Алгоритм нахождения ядра и образа оператора:

1. Пусть - линейный оператор, – матрица оператора в фиксированном базисе. Ядро оператора совпадает с множеством решения однородной системы 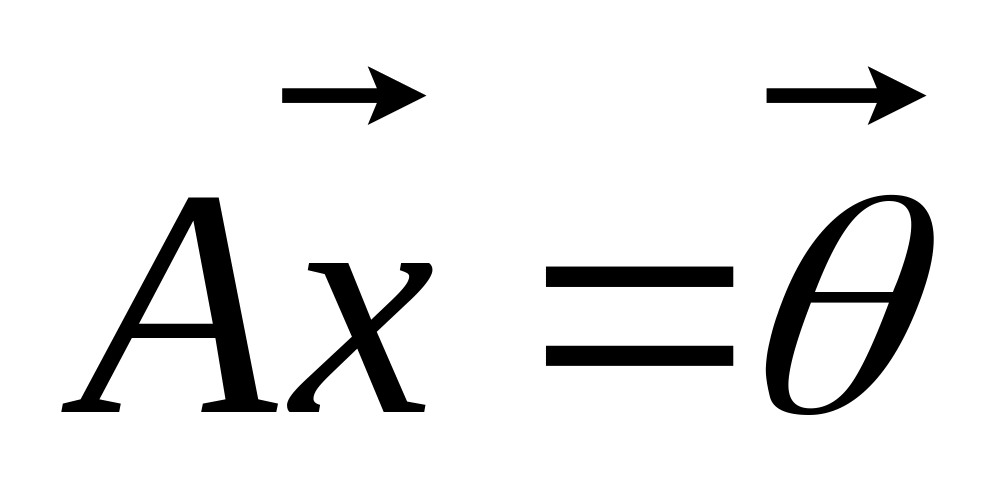, отсюда следует, что если 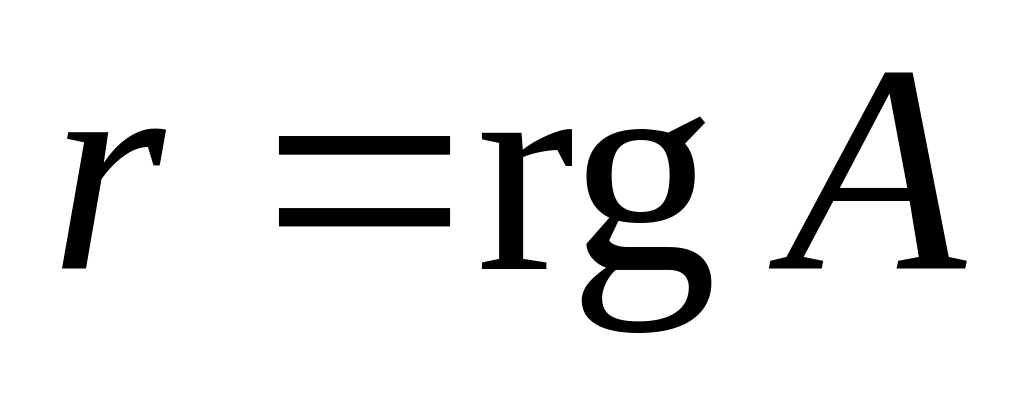, то .

2. Образ оператора совпадает с линейной оболочкой: 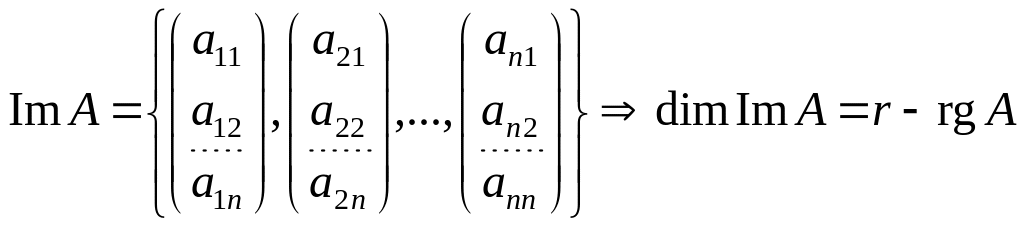. Пусть . Тогда 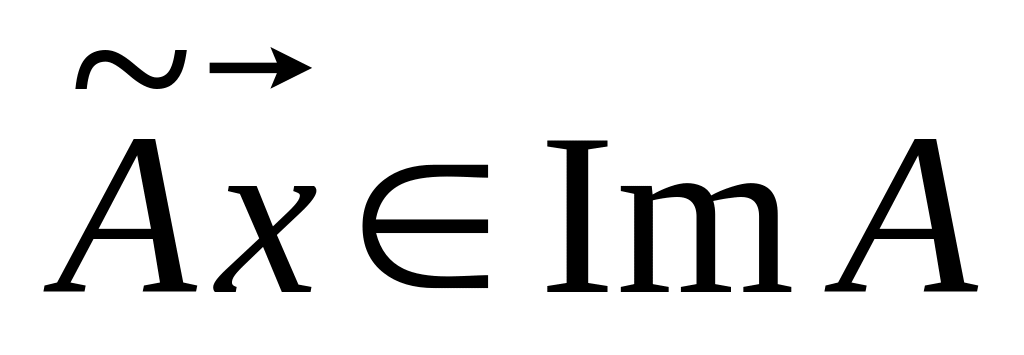и пусть 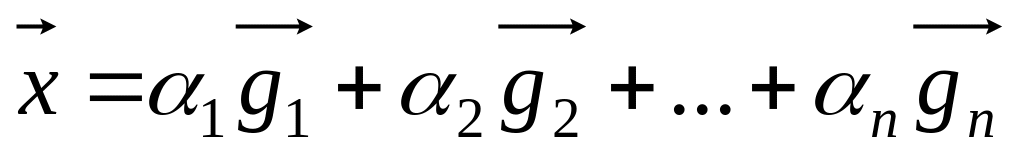в том же базисе, в котором дана матрица оператора. Тогда . Это означает, что .

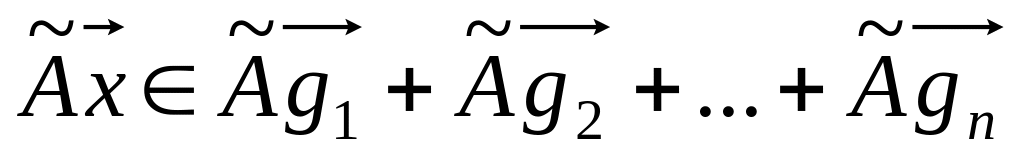, где n – размерность пространства, в котором действует оператор.

Размерность образа оператора называется размерностью оператора.

Размерность ядра оператора называется дефектом оператора.

Линейный оператор A называют невырожденным, если (т.е. дефект равен 0).

Суммой операторов A и B называют оператор C такой, что . Обозначение: .

Произведением операторов A и B называют оператор обозначение: .

Сумма и произведение линейных операторов является линейным оператором.

Матрица суммы линейных операторов равна сумме матриц этих операторов, матрица произведения – произведению матриц.

Обратный оператор

Линейный оператор B называется обратным для оператора A, если , где E – единичный оператор.

Для того чтобы линейный оператор A имел обратный, необходимо и достаточно, чтобы он был невырожденным, т.е. .

1. Пусть для любого A существует обратный и пусть 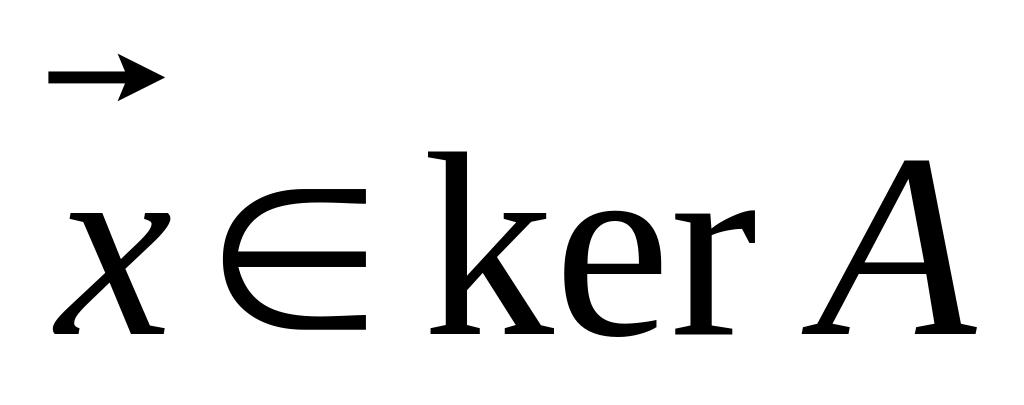. Это означает, что . Подействуем на обе части этого равенства обратным оператором: 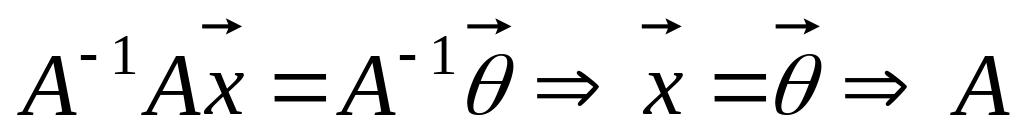невырожденный.

2. Пусть и пусть – матрица оператора в некотором базисе. По теореме о матрице оператора . Т.к. A невырожденный, то только при – невырожденная матрица, следовательно, существует ей обратная. Будем рассматривать матрицу как матрицу оператора B в том же базисе. Тогда .

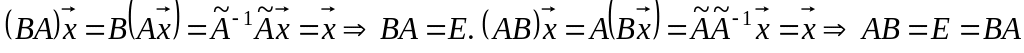Если A – матрица невырожденного оператора в каком-либо базисе, то – матрица обратного оператора в этом же базисе.

Собственные векторы и собственные числа

Ненулевой вектор называется собственным вектором линейного оператора A, если . При этом  – собственное число оператора A, соответствующее .

Теорема о собственных числах: Если  – собственное число оператора , то  ­– корень уравнения , где A – матрица оператора в некотором базисе.

Пусть  – собственное число оператора и A – матрица этого оператора в некотором базисе, а - собственный вектор, соответствующий числу . По определению , т.к. .

Уравнение – характеристическое.

Алгоритм нахождения собственных чисел:

1. Решая характеристическое уравнение, находим собственные числа оператора.

2. Для каждого собственного числа ищем собственный вектор.

Собственные векторы линейного оператора , отвечающие собственному числу , образуют вместе с линейное подпространство в .

Следует из того, что собственные векторы, отвечающие числу , образуют множество решения однородной системы , где – матрица оператора A.

Если – собственный вектор оператора A, отвечающий собственному числу , то и - собственный вектор, отвечающий числу  при   0.

Пусть – собственный и  – собственное число оператора A. Тогда – собственный вектор оператора A, отвечающий собственному числу .