Подпространство линейного пространства

Подпространством линейного пространства является часть пространства, которая сама является линейным пространством.

Второе определение: Подпространством линейного пространства является часть пространства, которая замкнута относительно операций, введённых в линейном пространстве.

Любое подпространство содержит нулевой элемент.

Линейной оболочкой векторов называют множество линейных комбинаций этих векторов. Обозначение линейной оболочки векторов .

Линейная оболочка является подпространством.

Пусть – линейная оболочка векторов и пусть , т.е. . Тогда , ­– подпространство.

Если – линейная комбинация , то .

Введём обозначения: . Пусть . Тогда . Т.к. является линейной комбинацией , то . Пусть теперь . Тогда и, следовательно, .

Максимальное число линейно независимых векторов системы называется рангом системы.

Размерность линейной оболочки векторов равна рангу системы этих векторов.

Пересечение и сумма подпространств.

Пересечением подпространств и называют множество векторов, принадлежащих и , и . Обозначение: .

Суммой подпространств и называют множество векторов вида , где . Обозначение: .

Сумма и пересечение подпространств являются пространствами.

Пусть . Тогда и , следовательно, и . Оставшаяся часть теоремы доказывается аналогично.

Теорема о связи размерностей пересечения и суммы подпространств: .

Прямая сумма подпространств

Сумма подпространств и называется прямой, если .

Теорема: , т.к. .

Любой элемент из может быть единственным образом представлен в виде , где .

Пусть , где и , где . Тогда . Но , а , и так как эти элементы можно сравнить, то и , следовательно, , что противоречит условию.

Линейные операторы

Оператор – это правило, по которому элементам одного линейного пространства ставятся в соответствие элементы другого или того же линейного пространства.

Оператор A называется линейным, если:

или .

Матрица линейного оператора:

Пусть дан линейный оператор (преобразует элемент n-мерного пространства в элемент n-мерного пространства).

1. Выберем в базис .

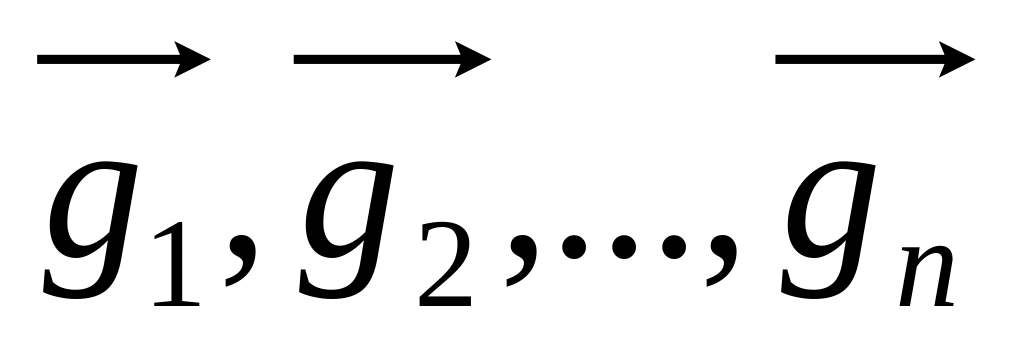2. Подействуем на базисные векторы оператором .

3. Разложим образы векторов по данному базису: .

4. Запишем координаты образов базисных векторов в виде столбцов матрицы: . Это и есть матрицы оператора A.

I теорема о матрице линейного оператора: Пусть под действием оператора A переходит в . Тогда 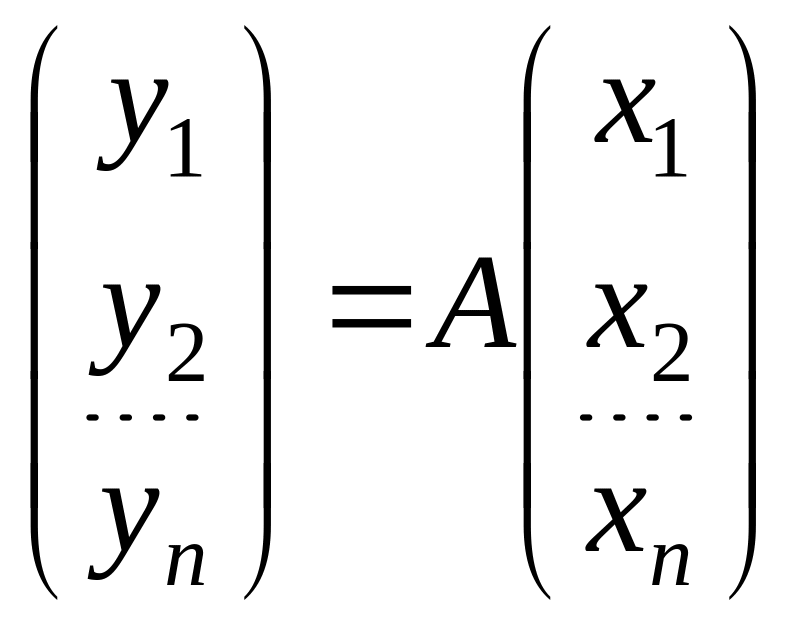, где A – матрица оператора A в том же базисе, в котором заданы координаты и .

Пусть – базис, в котором заданы и A. Тогда 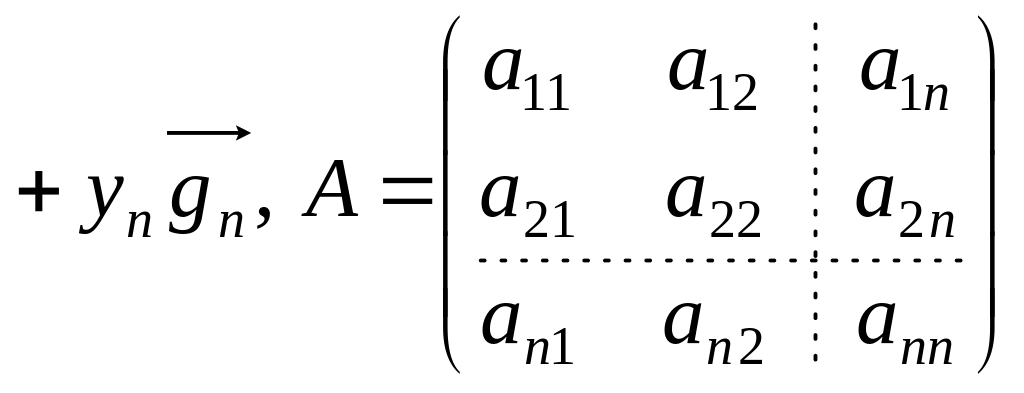. Подействуем на оператором A. В результате будет: .

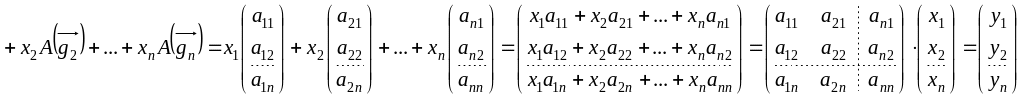Мы показали, что каждому линейному оператору в данном базисе соответствует матрица и можно показать, что она единственная. Также можно показать, что каждой матрице соответствует единственный линейный оператор.

II теорема о матрице линейного оператора: Пусть оператор в базисе имеет матрицу A, а базисе - матрицу . Тогда , где T – матрица перехода из базиса к базису .

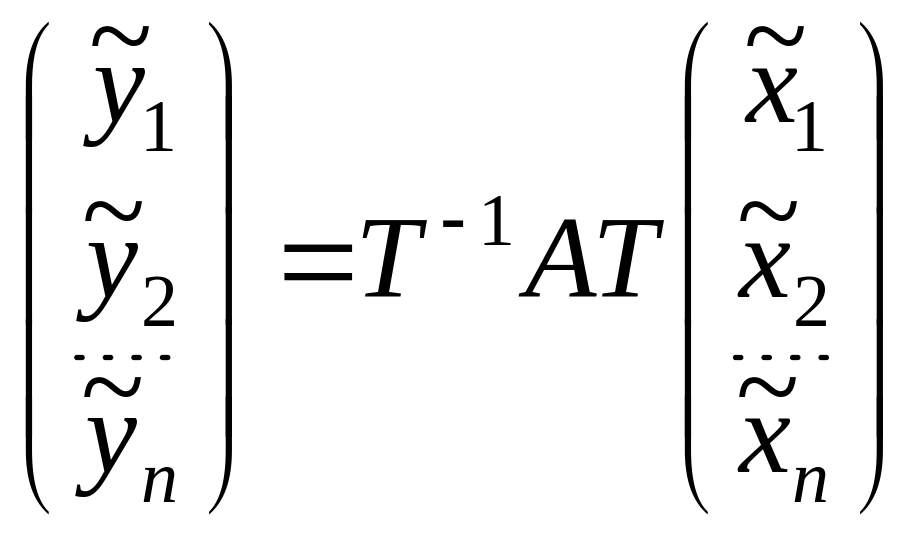Пусть в базисе имеет координаты , а в базисе , а – в , а в . Тогда , откуда . Следовательно, .