
- •II семестр
- •Элементарные преобразования матрицы
- •Ранг матрицы
- •Системы линейных алгебраических уравнений
- •Линейные пространства.
- •Линейная зависимость и линейная независимость векторов линейных пространств.
- •Подпространство линейного пространства
- •Ядро, образ, ранг, дефект.
- •Операторы простой структуры
- •Координаты вектора в ортонормированном базисе
- •Матрица Грама
- •Ортогональное дополнение к подпространству
- •Ортогональные операторы
- •Самосопряжённые операторы
- •Квадратичная форма
- •Канонический вид квадратичной формы
- •Знакопостоянные квадратичные формы
- •Приведение общего уравнения кривой второго порядка к каноническому виду
Линейные пространства.
Линейным пространством называется множество L элементов любой природы, если для элементов этого множества выполняются одно условие и восемь аксиом:
Условие: для
![]() и
и
![]() определена операция сложения, т.е. задано
правило, по которому любым
определена операция сложения, т.е. задано
правило, по которому любым
![]() и
и
![]() ставится в соответствие элемент
ставится в соответствие элемент
![]() ,
где символ «+» – только обозначение, и
для
,
где символ «+» – только обозначение, и
для
![]() и любого числа
определена операция
умножения
и любого числа
определена операция
умножения
![]() ,
т.е. задано правило, по которому каждому
и
ставится в соответствие элемент
,
т.е. задано правило, по которому каждому
и
ставится в соответствие элемент
![]() .
.
Аксиомы:
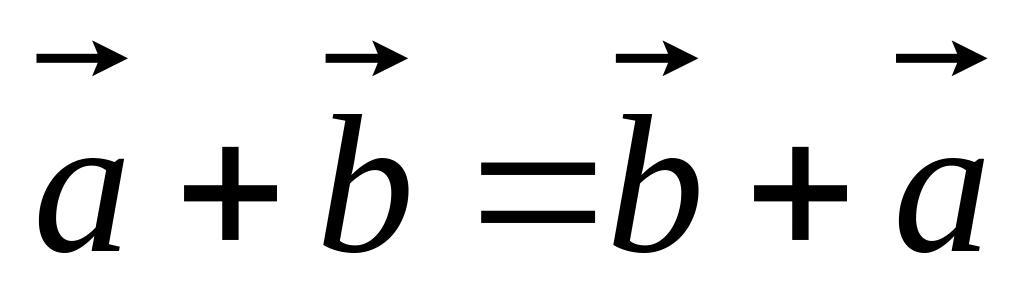 для
для
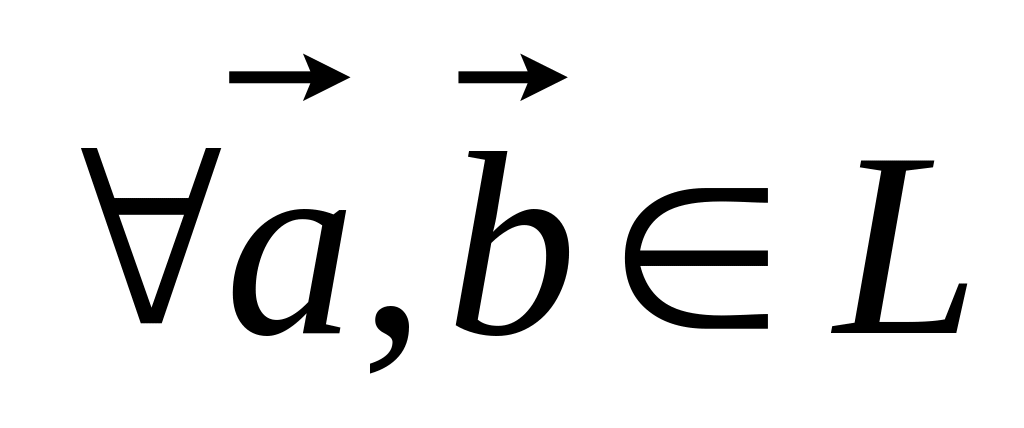 .
.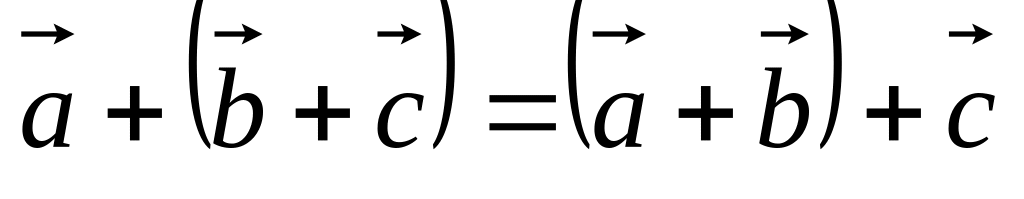 для
для
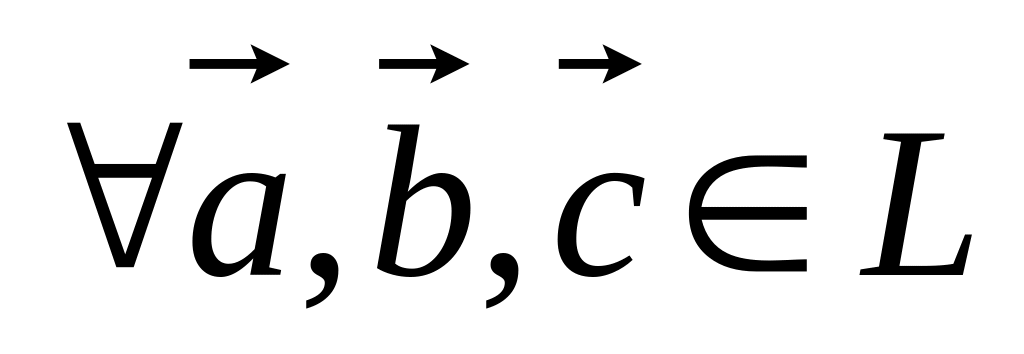 .
.Во множестве L
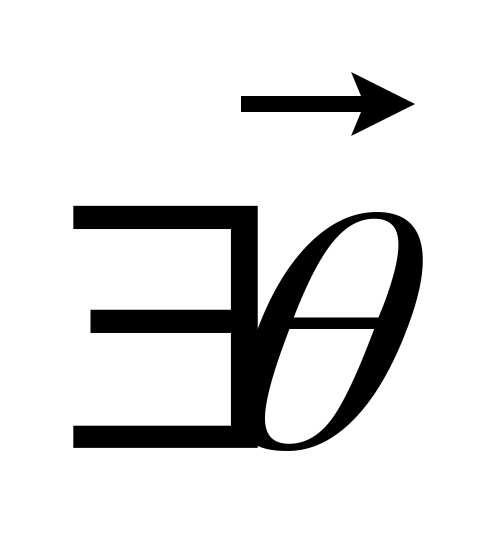 (нулевой (нейтральный) элемент):
(нулевой (нейтральный) элемент):
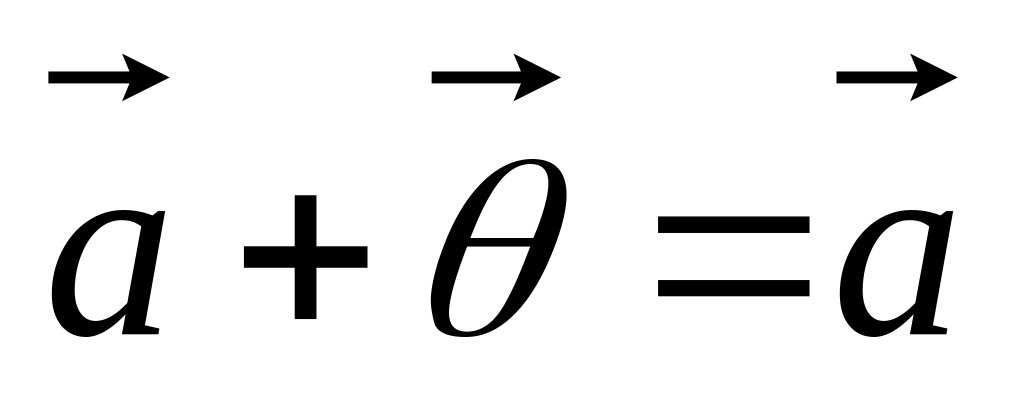 для
.
для
.Для
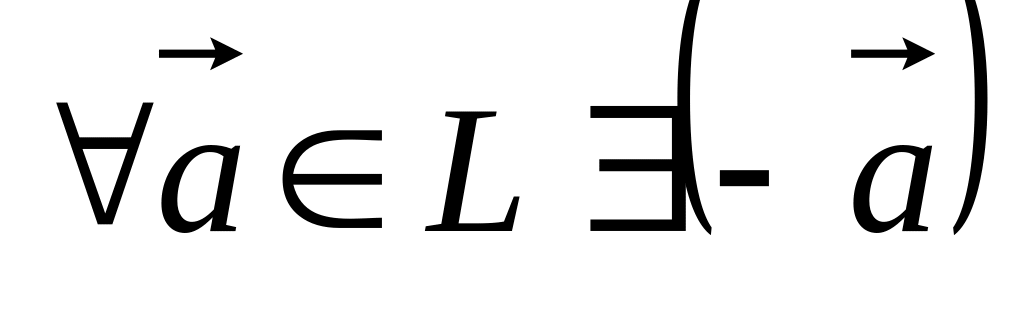 (противоположный элемент):
(противоположный элемент):
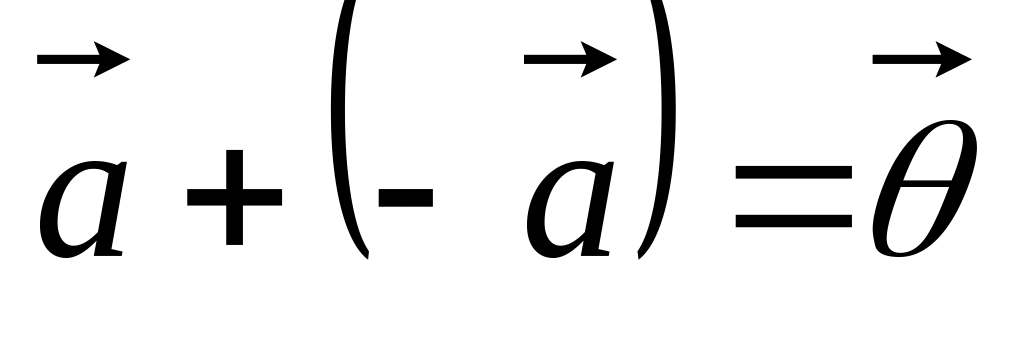 .
.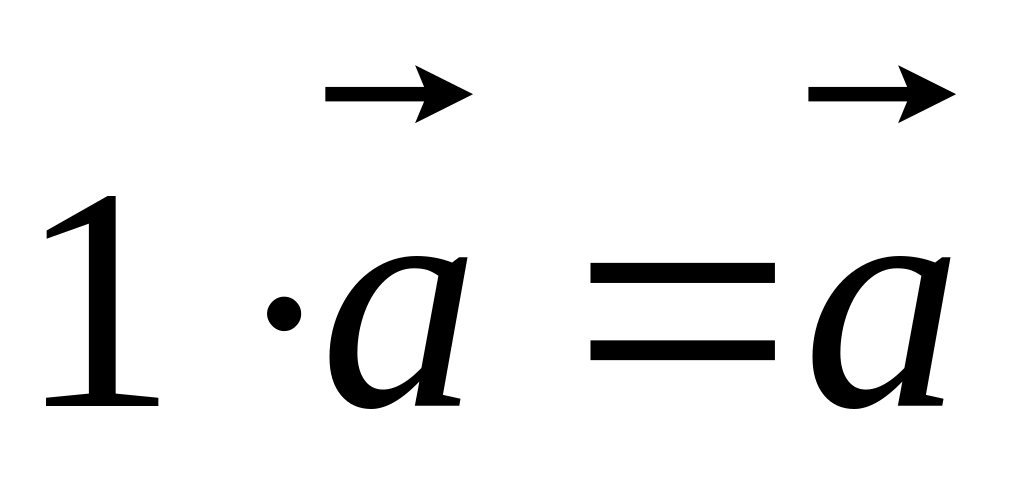 для
.
для
.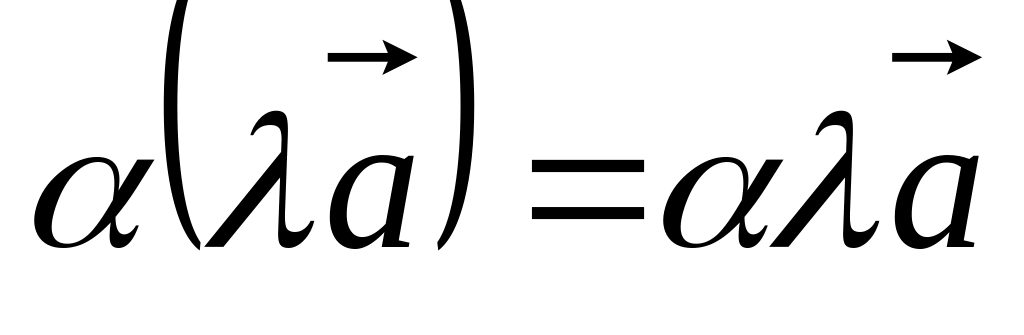 для
для
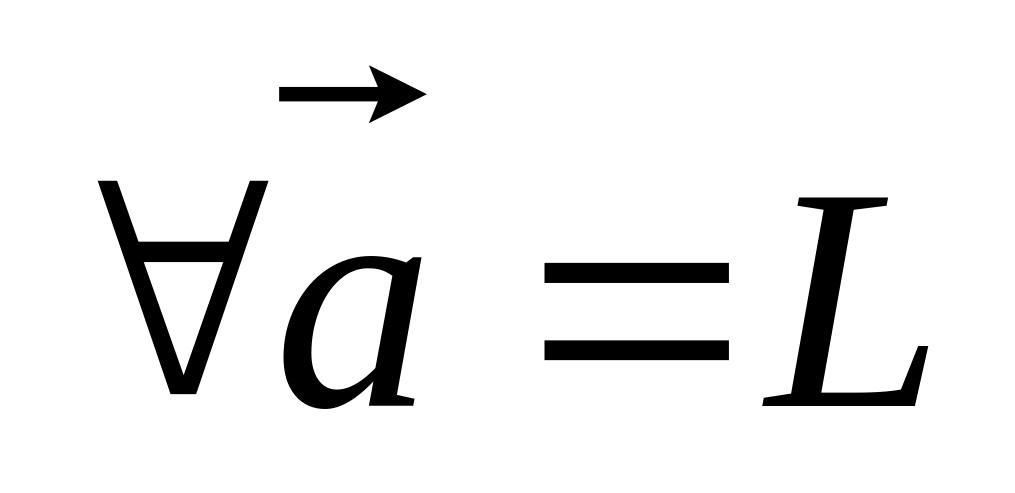
и
- числа.
и
- числа.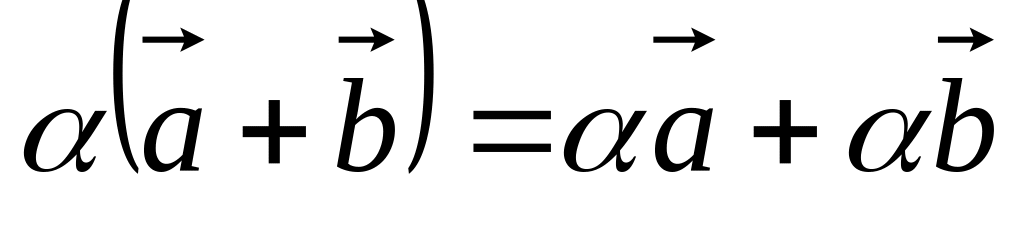 для
и
и любого числа .
для
и
и любого числа . для
,
и
- числа.
для
,
и
- числа.
Если данное множество является линейным пространством, то его элементы называются векторами.
Линейная зависимость и линейная независимость векторов линейных пространств.
Система векторов
![]() называется линейно независимой, если
хотя бы один из этих векторов можно
выразить через остальные, т.е.
называется линейно независимой, если
хотя бы один из этих векторов можно
выразить через остальные, т.е.
![]() .
.
Необходимо и достаточное условие
линейной зависимости: Для
того чтобы система векторов
![]() была линейно зависимой, необходимо и
достаточно, чтобы существовали числа
была линейно зависимой, необходимо и
достаточно, чтобы существовали числа
![]() ,
не все равные 0 и такие, что
,
не все равные 0 и такие, что
![]() .
.
Пусть система линейно зависима. Тогда
 ,
причём
,
причём
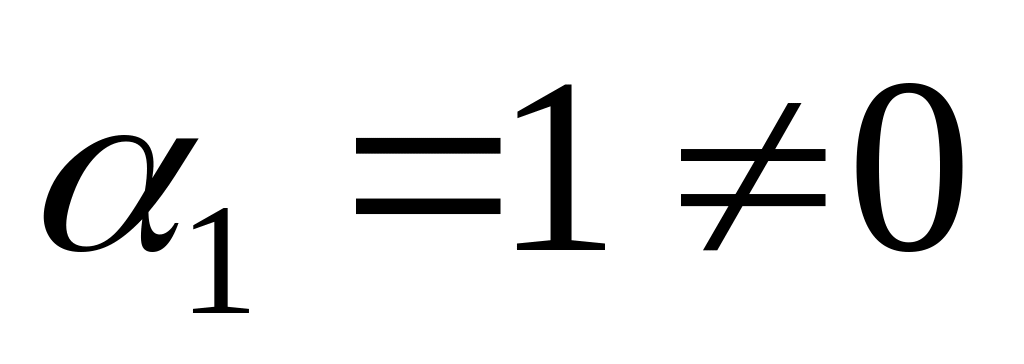 .
.Пусть
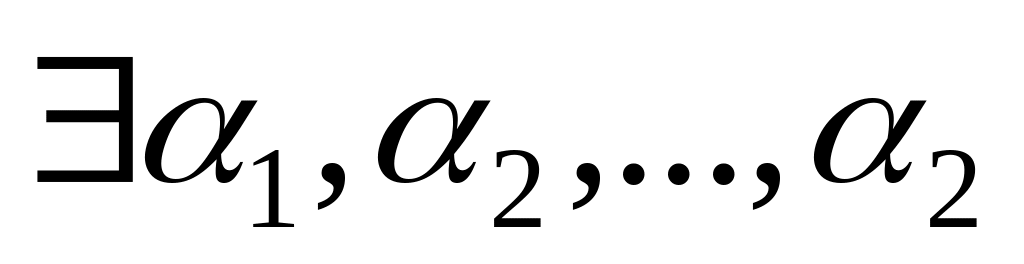 ,
не все равны 0 и такие, что
,
не все равны 0 и такие, что
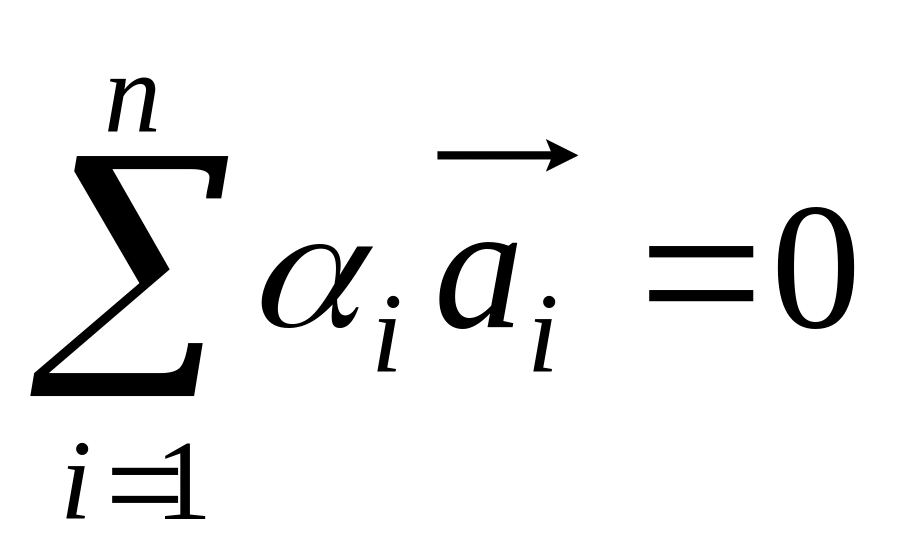 .
Пусть для определённости
.
Пусть для определённости
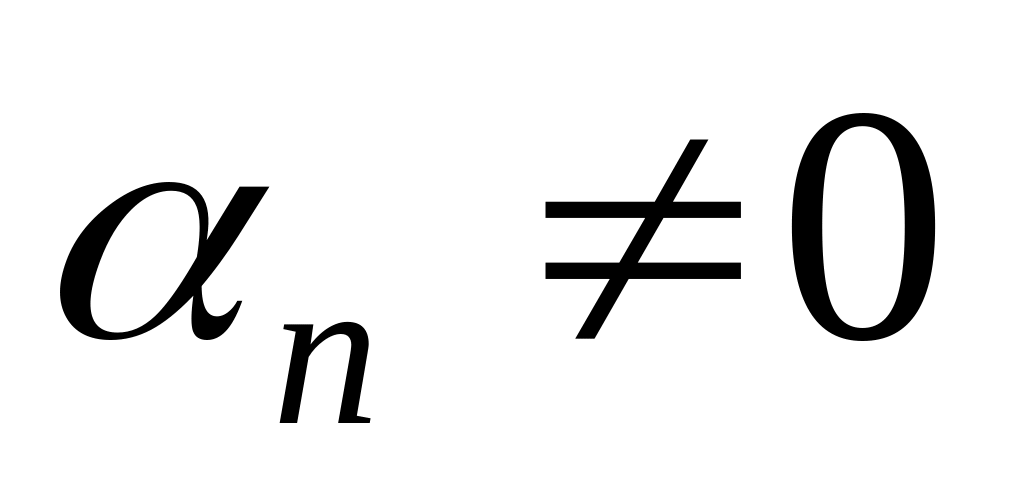 .
Тогда
.
Тогда
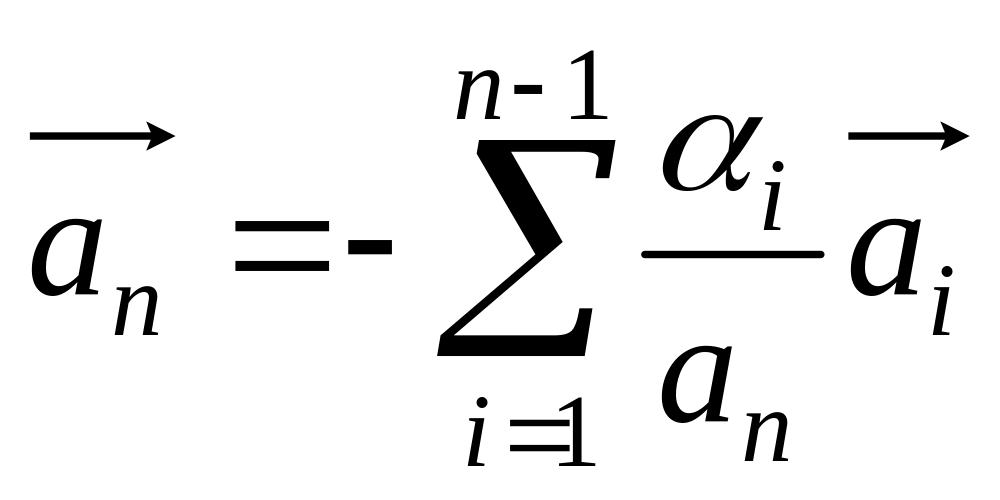 ,
следовательно, система линейно
независима.
,
следовательно, система линейно
независима.
Если среди
![]() содержится
содержится
![]() ,
то система векторов линейно зависима.
,
то система векторов линейно зависима.
Если среди k
векторов имеется m
линейно зависимых
![]() ,
то и вся система векторов линейно
зависима.
,
то и вся система векторов линейно
зависима.
Необходимое и достаточное условие
линейной независимости: Для
того чтобы система векторов
![]() были линейно независимой, необходимо
и достаточно, чтобы равенство
были линейно независимой, необходимо
и достаточно, чтобы равенство
![]() только при
только при
![]() для
для
![]() .
.
Если k векторов линейно независимы, то и любые m из них также линейно независимы.
Размерность линейного
пространства равна количеству базисных
векторов. Обозначение:
![]() .
Здесь n
– размерность.
.
Здесь n
– размерность.
Базисом в линейном пространстве называют систему векторов, если она удовлетворяет двум условиям:
Система линейно независимая.
Любой вектор пространства может быть линейно выражен через векторы этой системы.
Если в линейном пространстве имеется базис, состоящий из n векторов, то и любой другой базис также содержит n векторов.
Линейное пространство, в котором базис состоит из конечного числа векторов, называется конечномерным.
Число векторов в базисе называется размерностью линейного пространства. Обозначение: – линейное пространство размерностью n.
Если в пространстве выбран базис, то любой вектор этого пространства может быть представлен в виде линейной комбинации базисных векторов единственным образом.
Предположим, что в базисе
![]() вектор может быть представлен двумя
способами:
вектор может быть представлен двумя
способами:
![]() и
и
![]() .
Вычтем второе уравнение из первого:
.
Вычтем второе уравнение из первого:
![]() .
Т.к. здесь
.
Т.к. здесь
![]() ,
то
– линейно зависимы, что противоречит
условию.
,
то
– линейно зависимы, что противоречит
условию.
Пусть
![]() .
Тогда
.
Тогда
Любые m векторов (m > n) будут линейно зависимыми.
Любые n линейно независимых векторов образуют базис.
Пусть в пространстве выбран
базис
и пусть
![]() – разложение произвольного
– разложение произвольного
![]() по этому базису. Тогда коэффициенты
по этому базису. Тогда коэффициенты
![]() называют координатами
в базисе
.
называют координатами
в базисе
.
Пусть в
выбраны два базиса:
![]() и
и
![]() .
Назовём первый базис «старым», а второй
– «новым». Выразим базисные векторы
нового базиса через старый:
.
Назовём первый базис «старым», а второй
– «новым». Выразим базисные векторы
нового базиса через старый:
![]() .
Матрица
.
Матрица
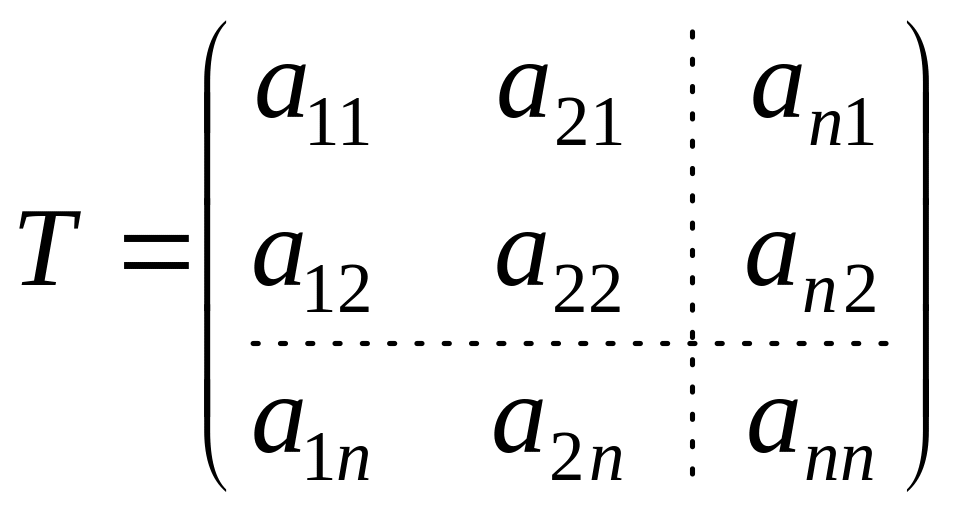 – матрица перехода от базиса
к базису
.
– матрица перехода от базиса
к базису
.
Теорема о замене базиса: Пусть
– произвольный вектор
и
– координаты
в базисе
![]() – координаты
в базисе
– координаты
в базисе
![]() .
Тогда
.
Тогда
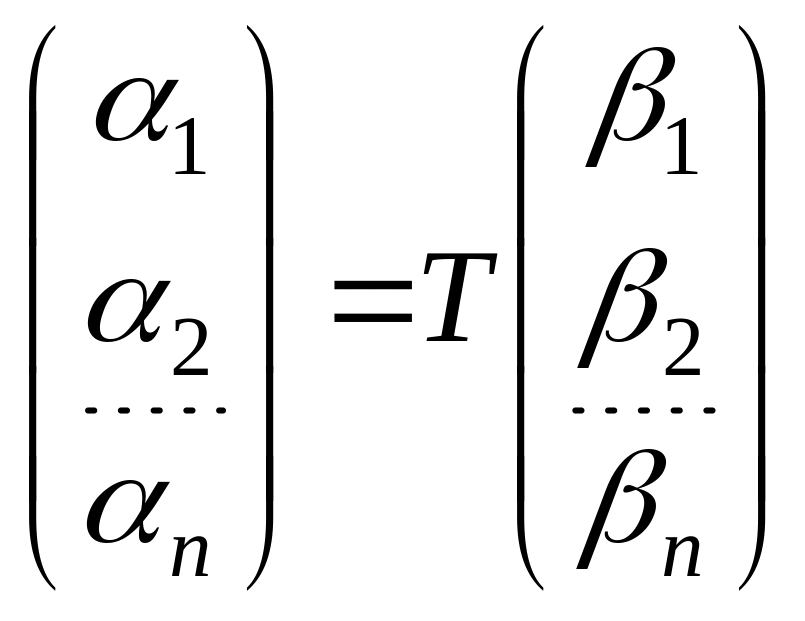 ,
где T
– матрица перехода от базиса
к базису
.
,
где T
– матрица перехода от базиса
к базису
.
Разложим
по базисам
и
:
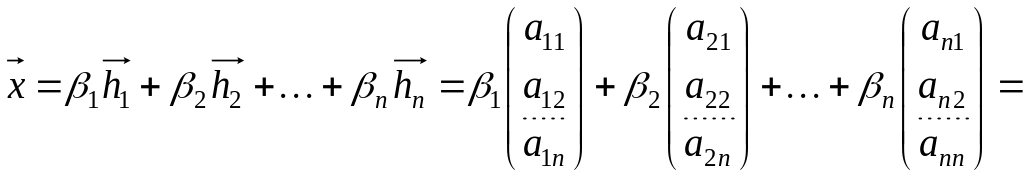
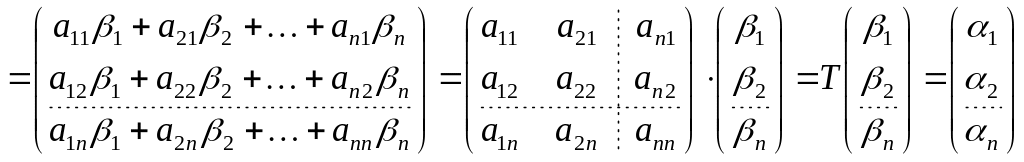 ,
где
,
где
![]() – j-я координата
– j-я координата
![]() в базисе
в базисе
![]() .
.
