
- •II семестр
- •Элементарные преобразования матрицы
- •Ранг матрицы
- •Системы линейных алгебраических уравнений
- •Линейные пространства.
- •Линейная зависимость и линейная независимость векторов линейных пространств.
- •Подпространство линейного пространства
- •Ядро, образ, ранг, дефект.
- •Операторы простой структуры
- •Координаты вектора в ортонормированном базисе
- •Матрица Грама
- •Ортогональное дополнение к подпространству
- •Ортогональные операторы
- •Самосопряжённые операторы
- •Квадратичная форма
- •Канонический вид квадратичной формы
- •Знакопостоянные квадратичные формы
- •Приведение общего уравнения кривой второго порядка к каноническому виду
Линейная алгебра
II семестр
Основные понятия
Матрицей порядка m
на n
называют прямоугольную таблицу чисел,
состоящую из m
строк и n
столбцов. Общий вид:
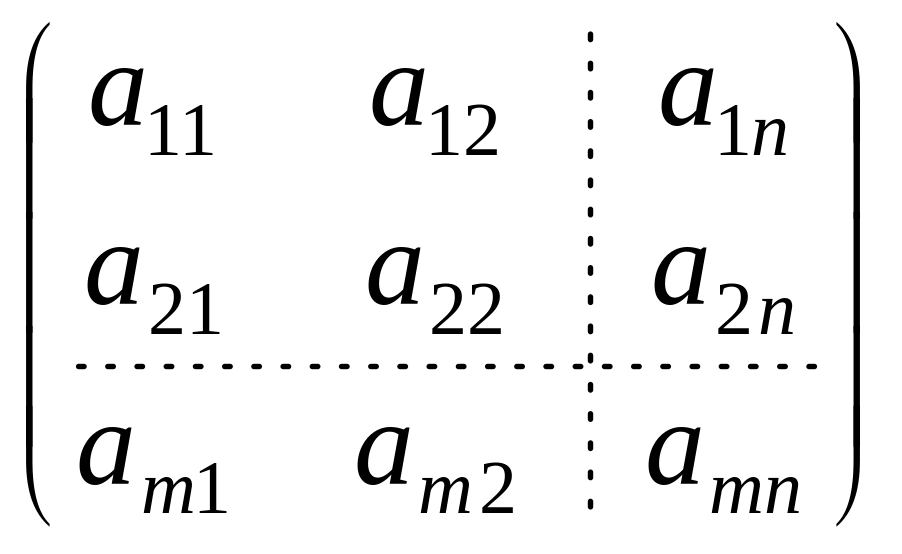 .
Также такая матрица обозначается как
.
Также такая матрица обозначается как
![]() .
Число
.
Число
![]() называется элементом матрицы. Числа i
и j обозначают
соответственно строку и столбец, в
которых этот элемент находится.
называется элементом матрицы. Числа i
и j обозначают
соответственно строку и столбец, в
которых этот элемент находится.
Если число строк матрицы равно числу столбцов, то такая матрица называется квадратной.
Главной диагональю квадратной
матрицы
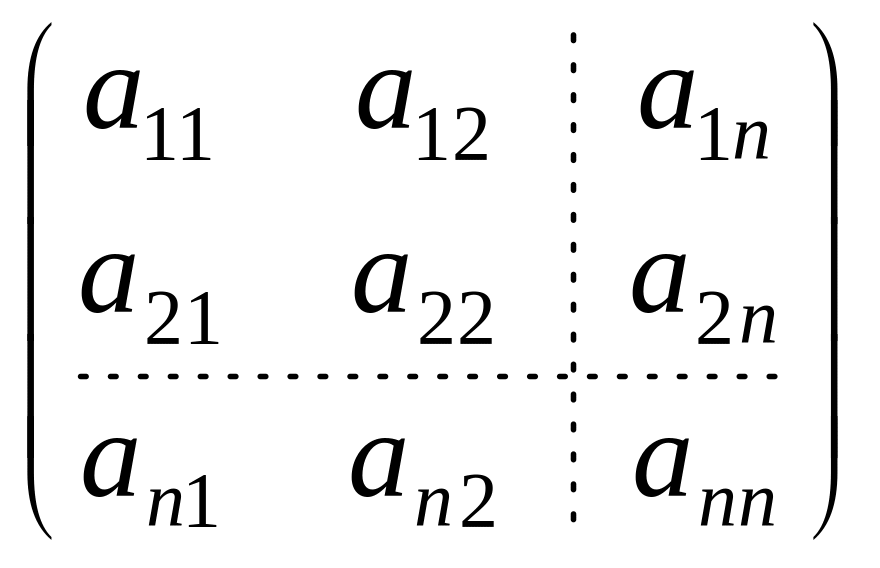 называют диагональ
называют диагональ
![]() .
.
Квадратная матрица называется
верхней треугольной, если все элементы
этой матрицы, лежащие ниже главной
диагонали равны нулю:
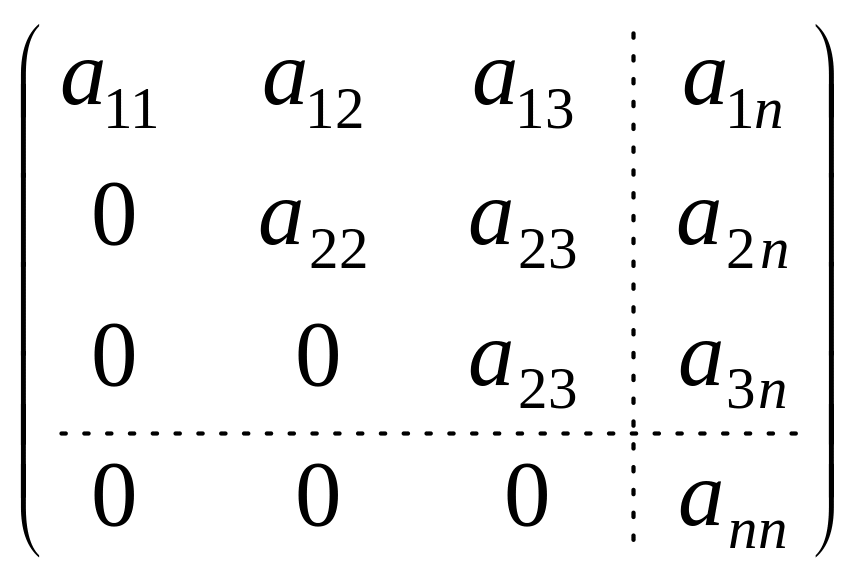 .
.
Квадратная матрица называется
диагональной, если все элементы этой
матрицы, лежащие вне главной диагонали,
равны нулю:
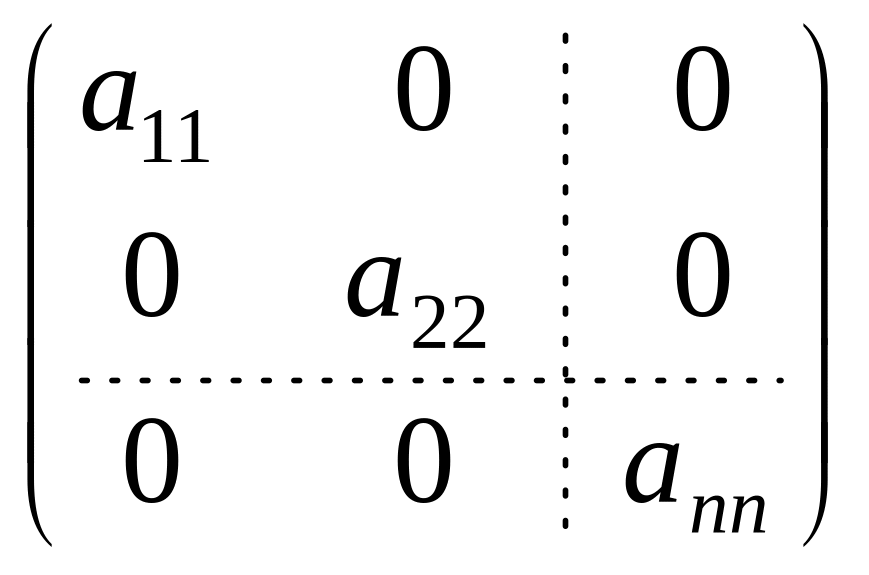 .
.
Если все элементы матрицы равны между собой, то такую матрицу называют скалярной.
Если элементы диагональной матрицы равны единице, то такую матрицу называют единичной, если нулю – нулевой.
Матрица-строка (или
вектор-строка):
![]() .
.
Матрица-столбец (или
вектор-столбец):
![]() .
.
Трапециевидная матрица:
 .
.
Две матрицы называют равными, если они одного размера и их соответствующие элементы равны.
Действия над матрицами
Сложение матриц:
 .
.
Свойства операции сложения:
![]() ,
,
![]() .
.
Умножение матрицы на число:
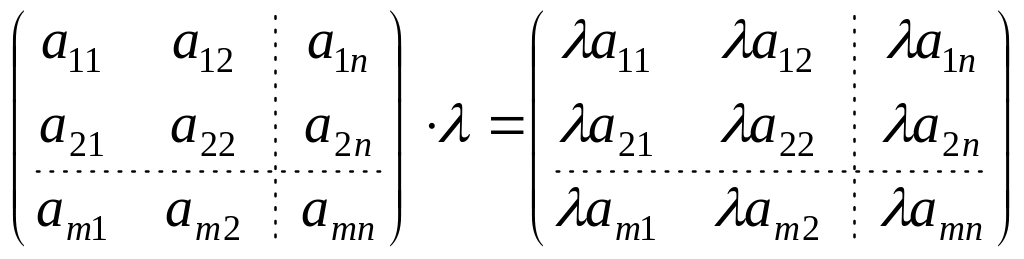 .
.
Две матрицы, взятые в определённом порядке, называются согласованными, если число столбцов первой матрицы равно числу строк второй.
Перемножать можно только согласованные матрицы.
Произведением матриц
![]() и
и
![]() называют матрицу
называют матрицу
![]() ,
где
,
где
![]() .
При этом в общем случае
.
При этом в общем случае
![]() .
.
Две матрицы A
и B
называют коммутирующими, если
![]() .
.
Транспонирование матрицы – преобразование,
при котором все столбцы матрицы заменяются
столбцами, а столбцы – строками.
Обозначение:
![]()
Свойства транспонирования:
![]() ,
,
![]() ,
,
![]() .
.
Числовые характеристики матриц
Определитель – числовая характеристика
только квадратных матриц. Обозначение:
![]() ,
,
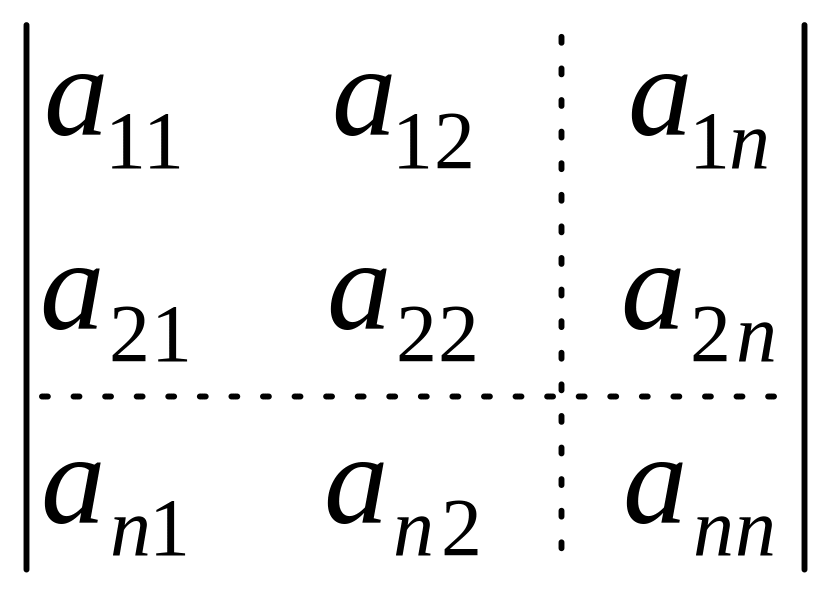 .
.
Если в прямоугольной матрице выбрать k строк и k столбцов, то на их пересечении будет лежать квадратная матрица k-го порядка. Определитель этой матрицы называется минором k-го порядка большой матрицы.
Минор элемента квадратной матрицы можно получить, вычеркнув ту строчку и столбец, в которой располагается этот элемент и составив из оставшихся элементов квадратную матрицу. Тогда этот элемент называется алгебраическим дополнением минора, а минор – алгебраическим дополнением элемента.
Матрица называется невырожденной, если её определитель не равен 0.
Определитель квадратной матрицы
вычисляется с помощью рекуррентного
соотношения:
![]() ,
где
,
где
![]() - минор элемента
.
(разложение по i-й
строке (или по j-му
столбцу)).
- минор элемента
.
(разложение по i-й
строке (или по j-му
столбцу)).
Свойства определителя:
Определитель матрицы при транспонировании не меняется, следовательно если какое-либо свойство доказано для строк, то оно доказано и для столбцов.
Если поменять местами две строки (или два столбца), то определитель сохранит своё абсолютное значение, но поменяет знак.
Линейное свойство определителя: Пусть даны строки (столбцы)
 .
Сумма произведений этих строк (столбцов)
на произвольные числа называется
линейной комбинацией строк (столбцов).
Если j-й
столбец (i-я
строка) является линейной комбинацией
столбцов (строк)
.
Сумма произведений этих строк (столбцов)
на произвольные числа называется
линейной комбинацией строк (столбцов).
Если j-й
столбец (i-я
строка) является линейной комбинацией
столбцов (строк)
 ,
т.е. представляет собой выражение
,
т.е. представляет собой выражение
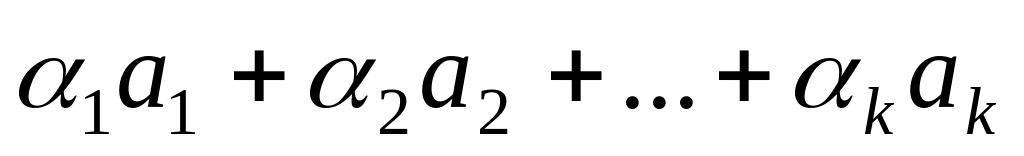 ,
то определитель этой матрицы равен
сумме определителей
,
то определитель этой матрицы равен
сумме определителей
 ,
где
,
где
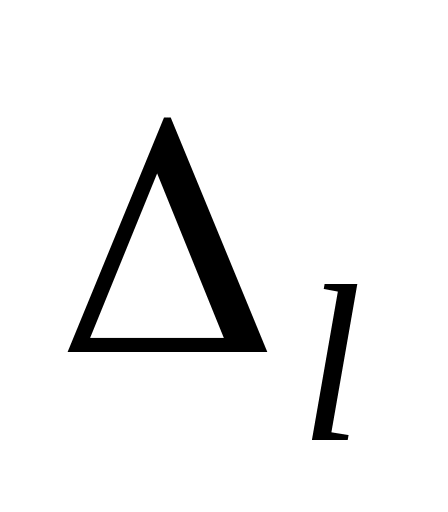 получается из исходного определителя
заменой j-го
столбца (i-й
строки) столбцом (строкой)
получается из исходного определителя
заменой j-го
столбца (i-й
строки) столбцом (строкой)
 .
.
Для доказательства рассмотрим случай,
когда j-й столбец есть
линейная комбинация двух столбцов:
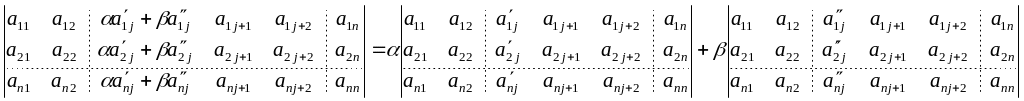 .
.
Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Если строку (столбец) умножить на какое-либо число, то и определитель умножится на это же число.
Если определитель содержит две пропорциональных строки (столбца), то он равен нулю.
Если все элементы одной из строк (столбцов) равны нулю, то и определитель равен нулю.
Если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на какое-либо число, то определитель не изменится.
Сумма произведений элементов одной строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю.
