25. Расчёт жб элементов по предельным состояниям первой группы.

При определении предельных усилий в сечении, нормальном к продольной оси, используют следующие предпосылки: сопротивление бетона растяжению Rbt =0, сопротивление бетона сжатию в пределах сжатой зоны принимается равным Rb (эпюра напряжений прямоугольная), максимальное растягивающее напряжение в арматуре равно Rs, сжимающее напряжение в арматуре принимается Rsc.

Граничное условие имеет вид: , значение вычисляется по формуле: 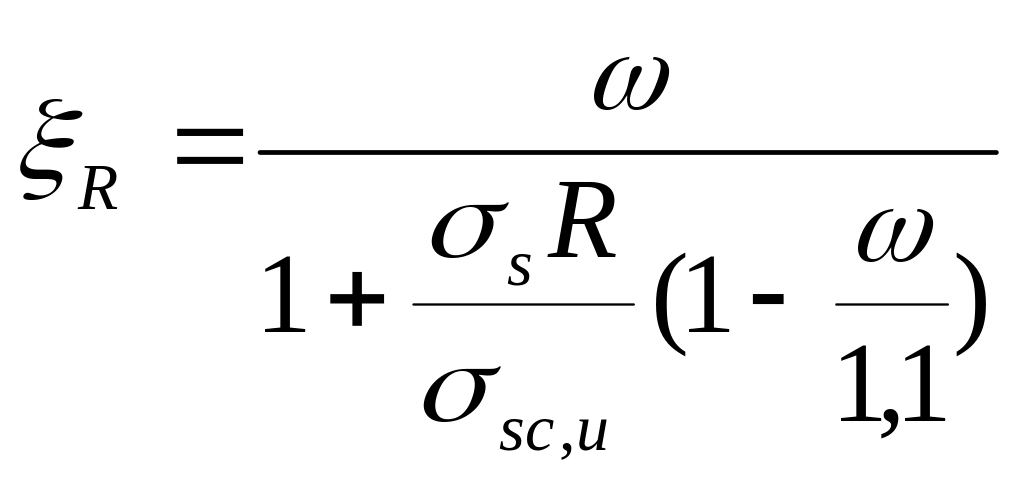, характеристика сжатой зоны бетона , .

Расчёт по прочности изгибаемых элементов в сечениях, нормальных к продольной оси. Расчет сечений при условии ведётся по формуле(для прямоугольного сечения): , высота сжатой зоны бетона х определяется: .

Тавровые сечения с полкой в сжатой зоне при рассчитываются: если граница сжатой зоны проходит в полке, то расчёт производится как и для прямоугольных сечений шириной , если граница сжатой зоны проходит в ребре: ,

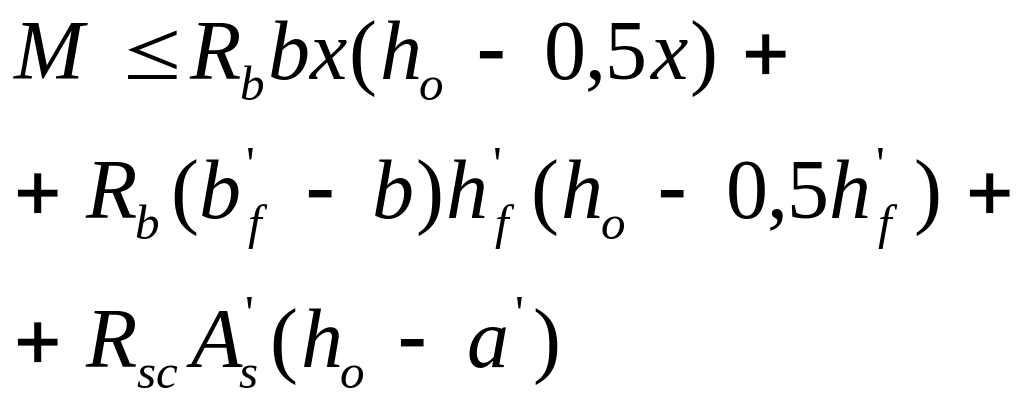При этом высота сжатой зоны бетона х определяется: . На практике расчёт ведётся: 1) определяется рабочая высота сечения , полная высота сечения . 2) рассчитывается площадь сечения арматуры As и проверяется условие .

3) вычисляют коэф армирования, по табл. по находят значение Ао и вычисляют М_f. После проверяют условие .

Расчёт по прочности сечений, наклонных к продольной оси элемента. Расчёт производится на действие поперечных сил и изгибающего момента. Проверяется условие , если оно выполняется, то расчёт на действие поперечной силы не требуется. Для обеспечения прочности необходимо, чтобы расчётные усилия M и Q не превышали несущей способности сечения:

,

. Значение Q_b для изгибаемых элементов с ненапрягаемой продольной арматурой определяется по эмпирической формуле: , где . Поперечная сила, воспринимаемая хомутами и бетоном сжатой зоны , вычисляется C_o и подставляется в основную формулу: 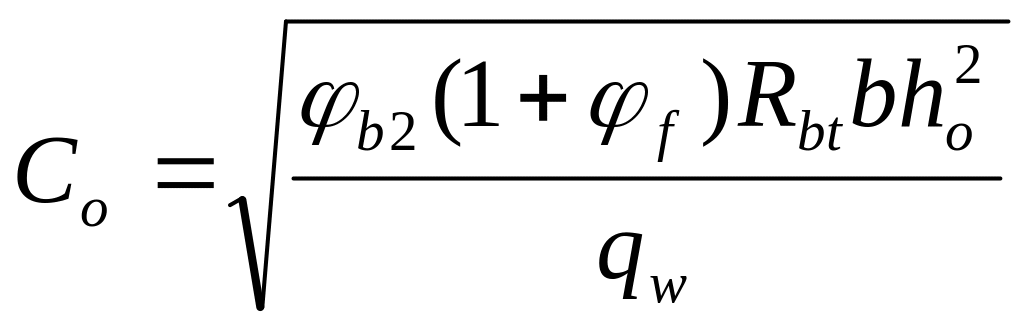, получаем , где - предельное усилие на единицу длины элемента.

Для изгибаемых предварительно напряженных, внецентренно сжатых и растянутых элементов: , где , но не более 0,5 и , но не более -0,8 – коэф, учитывающий влияние продольной силы. Суммарный коэф принимается не более 1,5.

26. Расчёт жб элементов по предельным состояниям второй группы.

По образованию нормальных трещин (в центрально-растянутых элементах):

при расчёте рассматривается состояние непосредственно предшествующее образованию трещин:

растягивающее напряжение в бетоне равное R_bt,ser, напряжение в напрягаемой арматуре равное предварительному напряжению с учётом всех потерь.

ЖБ элемент гарантирован от образования трещин, если продольная растягивающая сила, отвечающая сопротивлению сечения в состоянии, предшествующем образованию трещин в бетоне, не менее продольной силы, вычисленной при расчётных или нормативных значениях нагрузки. , где , , если без предварительного напряжения .

По образованию нормальных трещин (в изгибаемых, внецентренно растянутых и сжатых элементах):

При расчёте принимаются следующие предпосылки: эпюра напряжений в сжатой зоне бетона имеет криволинейное очертание, в растянутой зоне бетона – прямоугольное. Применяется метод расчёта по точкам поперечного сечения.

Расчёт производят по условию , -момент внешних сил, расположенных по одну сторону от рассматриваемого сечения: при изгибе , при внецентренном сжатии , при внецентренном растяжении , e - расстояние от центра тяжести приведенного сечения до точки приложения внешней продольной силы N, r – расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удалённой от растянутой зоны.

Момент M_crc : , где M_rp – момент усилия Р относительно оси, при которой вычисляют M_r, принимая знак, отвечающий направлению вращения, W_pl – упругопластический момент сопротивления приведенного сечения. Приближённо упругопластический момент сопротивления , коэффициент зависит от формы сечения (1,5…1,75). Расстояние r вычисляется .

Расчёт по образованию наклонных трещин:

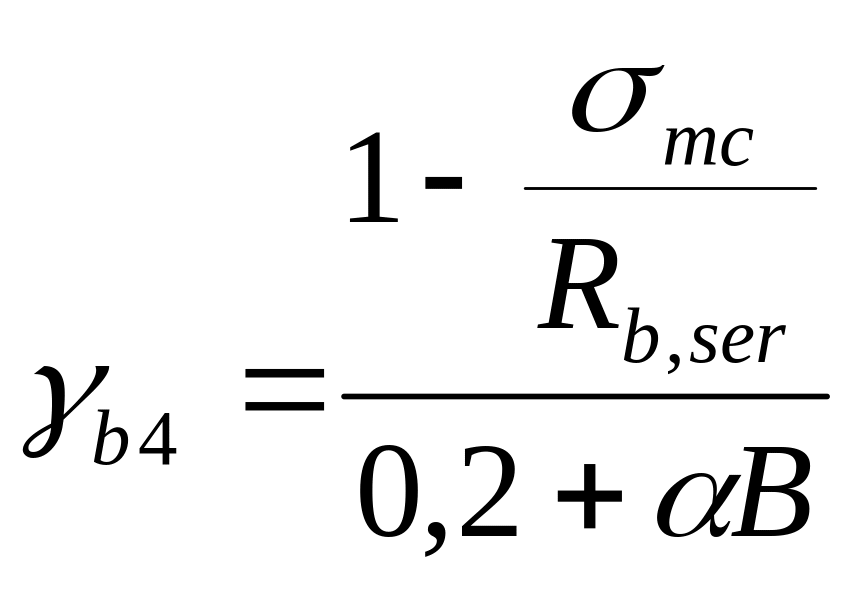Расчёт производится в тех местах, где действуют наибольшие растягивающие напряжения , с учётом главных сжимающих напряжений . Проверку выполняют по условию при , при , где , но не более 1, - для тяжёлого бетона 0,01; - для лёгких и ячеистых бетонов 0,02.

Значения главных напряжений вычисляются: ,

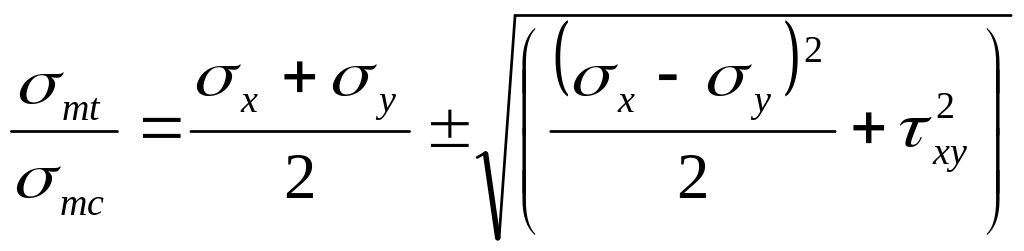, , , S_red – приведенный статический момент части сечения.

, - длина анкеровки.

Расчёт по деформациям: проверяется условие обеспечения жёсткости изгибаемого элемента: , где - подученное значение, - нормативное значение.

Кривизна оси: , прогиб: , где - коэффициент, зависящий от расчётной схемы элемента, кривизна оси в наиболее нагруженном сечении.

Расчёт по раскрытию трещин:

Ширина раскрытия трещин определяется на уровне центра тяжести наиболее растянутых арматурных стержней в общем виде: , по эмпирической зависимости , где - коэффициент равный 1 для изгибаемых и внецентренно сжатых элементов и 1,2 - для растянутых, - коэф, характеризующий длительность действия нагрузки, - коэф, учитывающий влияние вида рабочей арматуры, - коэф армирования (не более 0,02), d – диаметр растянутой арматуры, - напряжение в растянутой арматуре в сечении с трещиной, вычисляется для каждлгл вида деформаций, например для ценрально-растянутых элементов: .

Расчёт элементов по закрытию трещин: для изгибаемых, сжатых и внецентренно растянутых элементах трещины считаются закрытыми, если соблюдается условие ,

для центрально-растянутых элементов , Mnr – нормативный момент внешних сил, для изгибаемых элементов: , для внецентренно сжатых (растянутых) элементов: , где M_n и N_n - изгибающий момент и продольная сила от внешних нагрузок, - расстояние от ядровой точки до центра тяжести приведенного сечения. В продольной растянутой арматуре Аsp при полной нормативной нагрузке должно выполняться условие .