
- •Билет – 1 «основные понятия и определения статики»
- •Билет – 2 «аксиомы статики».
- •Билет – 3 «основные виды связей и их реакции».
- •Билет – 4 «сложение сходящихся сил. Силовой многоугольник. Условия равновесия сходящихся сил».
- •Билет – 5 «теорема о трех силах».
- •Билет – 6 «момент силы относительно точки».
- •Билет-7 «Аналитические выражения момента силы относительно координатных осей»
- •Билет-8 «Сложение параллельных сил. Пара сил. Момент пары.»
- •Билет-12 Условия равновесия произвольной пространственной системы сил
- •Билет – 14
- •Билет – 18 «методы расчета плоской фермы»
- •Билет – 19» «трения скольжения. Угол трения. Конус трения».
- •Билет – 20 «трение качения»
- •Билет-21 «Центр параллельных сил»
- •Б илет – 22 «центр тяжести. Общие формулы для определения центра тяжести однородных тел».
- •Билет – 23 «способы определения центра тяжести»
- •5.4. Частные случаи приведения системы сил.
Билет – 5 «теорема о трех силах».
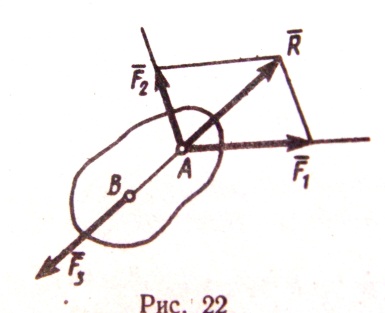
3)ТЕОРЕМА О ТРЕХ СИЛАХ – Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Для
доказательства теоремы рассмотрим
сначала какие-нибудь две из действующих
на тело сил, например ![]()
Т.к. по
условиям теоремы эти силы лежат в одной
плоскости и не параллельны, то их линии
действия пересекаются в некоторой точке
А. (РИС. 22) Приложим силы ![]() в этой точке и заменим их равнодействующей
.
Тогда, на тело будут действовать две
силы: сила
и сила
приложенная
в какой-то точке В тела. Если тело при
этом находиться в равновесии, то силы
и
должны быть направлены по одной прямой,
т.е. вдоль АВ. Следовательно, линия
действия силы
тоже проходит через точку А, что и
требовалось доказать.
в этой точке и заменим их равнодействующей
.
Тогда, на тело будут действовать две
силы: сила
и сила
приложенная
в какой-то точке В тела. Если тело при
этом находиться в равновесии, то силы
и
должны быть направлены по одной прямой,
т.е. вдоль АВ. Следовательно, линия
действия силы
тоже проходит через точку А, что и
требовалось доказать.
Билет – 6 «момент силы относительно точки».
Точку,
относительно которой берется момент,
называют ЦЕНТРОМ МОМЕНТА, а момент силы
относительно этой точки – МОМЕНТОМ
ОТНОСИТЕЛЬНО ЦЕНТРА. МОМЕНТОМ СИЛЫ ![]() ОТНОСИТЕЛЬНО ЦЕНТРА О – называется
приложенный в центре О вектор
ОТНОСИТЕЛЬНО ЦЕНТРА О – называется
приложенный в центре О вектор ![]()
![]() , модуль которого равен произведению
модуля F
силы на её плечо h
и который направлен перпендикулярно
плоскости, проходящей через центр О и
силу, в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг
центра О против хода часовой стрелки
(рис. 31).
, модуль которого равен произведению
модуля F
силы на её плечо h
и который направлен перпендикулярно
плоскости, проходящей через центр О и
силу, в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг
центра О против хода часовой стрелки
(рис. 31).

Билет-7 «Аналитические выражения момента силы относительно координатных осей»
Возьмем три взаимно перпендикулярные координаты оси x, y, z, которым соответствуют орты I, j, k.
Момент М0 силы Р относительно начала координат, выражается формулой
М0=r × P
Где r-радиус-вектор точки А приложения силы относительно начала координат.
Разложим вектор М0 на составляющие по осям координат:
М0=i×Mx+j×My+k×Mz
Из векторной алгебры известно, что векторное произведение r×P можно представить определителем:
i j k
r×P= x y z
X Y Z
Приравнивая значения М0 и определителя, разложенного по элементам первой строки, получаем
i×Mx+j×My+k×Mz=i×(y×Z-z×Y)+j×(z×X-x×Z)+k×(x×Y-y×X)
Сопоставляя левые и правые части этого равенства, находим проекции момента М0 на оси координат, равные моментам силы Р относительно этих осей
Mx=y×Z-z×Y; My=z×X-x×Z; Mz=x×Y-y×X.
Билет-8 «Сложение параллельных сил. Пара сил. Момент пары.»
Сложение
параллельных сил параллельные направленные
в одну сторону силы
![]() приложенные
в точках А и В.
приложенные
в точках А и В.
Согласно
1-й и 2-й аксиомам статики перейдем от
данной системы параллельных сил к
эквивалентной системе сходящихся сил
![]() .
Для этого приложим в точка А и В две
уравновешивающие силы
.
Для этого приложим в точка А и В две
уравновешивающие силы
![]() направленные
вдоль прямой АВ и сложим их с силами
по
правилу параллелограмма. Полученные
силы
перенесем
в точку О, где пересекаются их линии
действия и разложим на первоначальные
составляющие. Силы
направленные
вдоль прямой АВ и сложим их с силами
по
правилу параллелограмма. Полученные
силы
перенесем
в точку О, где пересекаются их линии
действия и разложим на первоначальные
составляющие. Силы
![]() отбросим
(по 2-й аксиоме статики) и останутся две
направленные по одной прямой силы
.
Эти силы переносим в точку С и заменяем
равнодействующей
отбросим
(по 2-й аксиоме статики) и останутся две
направленные по одной прямой силы
.
Эти силы переносим в точку С и заменяем
равнодействующей
![]() модуль
которой равен:
модуль
которой равен:
![]()
Для определения положения точки С рассмотрим треугольники ОаК, ОАС, ОСВ, Оbm. Из подобия
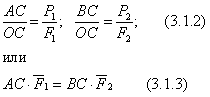
т.к.
![]() .
Далее учитывая свойства пропорций,
уравнение (3.1.1) и то, что
.
Далее учитывая свойства пропорций,
уравнение (3.1.1) и то, что
BC+AC=AB
получаем
![]()
Рассмотрим случай сложения параллельных сдал направленных в разные стороны.
Пусть
![]() .
.
Выберем
на продолжении прямой АВ точку С и
приложим к ней уравновешенные силы
![]() которые
параллельны
.
Положение точки С и модули сил выберем
таким образом, чтобы удовлетворялись
соотношения
которые
параллельны
.
Положение точки С и модули сил выберем
таким образом, чтобы удовлетворялись
соотношения
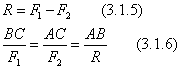
Складываем
силы
![]() и
и
![]() ,
согласно (3.1.1) и (3.1.4), получим их
равнодействующую
,
согласно (3.1.1) и (3.1.4), получим их
равнодействующую
![]() равную
по модулю
равную
по модулю
![]() ,
то есть модулю
,
то есть модулю
![]() и
приложенную в точке А. То есть силы
и
оказались
уравновешенными и их можно отбросить.
и
приложенную в точке А. То есть силы
и
оказались
уравновешенными и их можно отбросить.
В итоге силы заменяются одной силой , которая и является их равнодействующей. Точка приложения С равнодействующей и ее модуль определяются формулами (3.1.5), (3.1.6).
С помощью формул (3.1.1.) - (3.1.6) можно решать задачу о разложении силы на две ей параллельные. Задача будет определенной при задании дополнительных условий.
Пара
сил. Момент пары.Система
двух равных по модулю, параллельных и
противоположно направленных сил
![]() и
называется
парой сил. Система не находится в
равновесии, но и не имеет равнодействующей.
и
называется
парой сил. Система не находится в
равновесии, но и не имеет равнодействующей.
Плоскость, проходящая через линии действия сил называют плоскостью действия пары. Расстояние d между линиями действия сил пары называют плечом пары.
Действие пары сил на твердое тело сводится к вращательному эффекту и зависит от:
1) модуля F и длины плеча d;2) положения плоскости пары;3) направления поворота в этой плоскости.Для характеристики этого вращательного эффекта вводится понятие момент пары.
Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо.
![]() Момент
пары условимся считать положительным
(+), если пара стремится повернуть тело
против хода часовой стрелки, и отрицательным
(-) - когда по ходу часовой стрелки.
Момент
пары условимся считать положительным
(+), если пара стремится повернуть тело
против хода часовой стрелки, и отрицательным
(-) - когда по ходу часовой стрелки.
Обозначение
момента пары m или М без индекса имеет
свой смысл, так как момент пары нельзя
смешивать с моментом силы относительно
центра и этот центр указывается в индексе
(например:
![]() ).
Момент же пары определяется только
силами и плечом.
).
Момент же пары определяется только
силами и плечом.
Действие
пары сил, как уже указывалось выше,
характеризуется тремя условиями. При
характеристике пар необходимо задавать
все три значения. Но мы знаем, что
вектор-нормаль к плоскости задает
значения второго и третьего условия.
Если мы теперь пронормируем вектор-нормаль
значением момента пары, то все три
условия будут выполнены. Эти соображения
и позволили рассматривать момент пары
как вектор. Будем изображать момент
пары вектором
![]() или
или
![]() ,
модуль которого равен модулю момента
пары, и который направлен перпендикулярно
плоскости действия пары, в ту сторону
откуда поворот пары виден происходящим
против хода часовой стрелки.
,
модуль которого равен модулю момента
пары, и который направлен перпендикулярно
плоскости действия пары, в ту сторону
откуда поворот пары виден происходящим
против хода часовой стрелки.
Если рассматривать только пары лежащие в одной плоскости, то вместо вектора момента пары, можно стрелкой указывать только направлением поворота.Вектор на рис. 25 условно изображен выходящим из точек В и D, однако он может изображаться выходящим из середины АВ или CD или из произвольной точки плоскости действия пары, так как
![]()
БИЛЕТ – 9
«ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ ПАР».
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР: Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу. Это следует из того, что указанными операциями, т.е. путем изменения плеча и перемещения пары в плоскости действия или переноса в параллельную плоскость, пары с одинаковыми моментами могут быть преобразованы одна в другую.
БИЛЕТ – 10
«СЛОЖЕНИЕ ПАР»
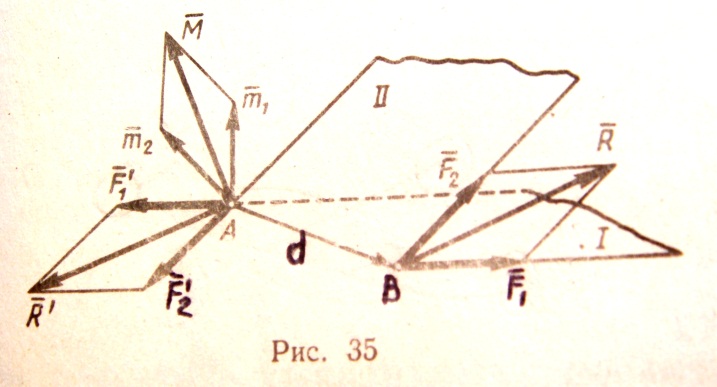
ТЕОРЕМА О СЛОЖЕНИИ ПАР: система пар, действующих на абсолютно твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар
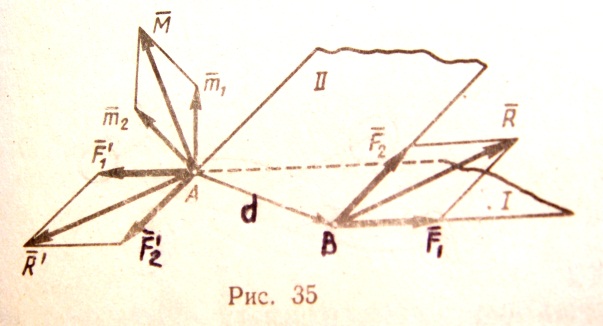
Рассмотрим
сначала две пары с моментами ![]() и
и ![]() , лежащие в плоскостях I
и II
(рис.35). Возьмем на линии пересечения
плоскостей отрезок АВ = d
и изобразим пару с моментом
силами
и
, лежащие в плоскостях I
и II
(рис.35). Возьмем на линии пересечения
плоскостей отрезок АВ = d
и изобразим пару с моментом
силами
и ![]() , а пару с моментом
- силами
и
, а пару с моментом
- силами
и ![]() . Сложив силы, приложенные в точках А и
В, убеждаемся, что пары
и
и
действительно эквивалентны одной паре
,
. Сложив силы, приложенные в точках А и
В, убеждаемся, что пары
и
и
действительно эквивалентны одной паре
, ![]() . Найдем момент
. Найдем момент ![]() этой пары. Так как
=
+
, то
этой пары. Так как
=
+
, то ![]() *
=
*
+
*
=
*
+![]() *
*![]() или
=
+
или
=
+
БИЛЕТ-11
Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил. Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.
О![]() сн
теор статики (теорема Пуансо): Всякую
пространственную систему сил в общем
случае можно заменить эквивалентной
системой, состоящей из одной силы,
приложенной в какой-либо точке тела
(центре приведения) и равной главному
вектору данной системы сил, и одной пары
сил, момент которой равен главному
моменту всех сил относительно выбранного
центра приведения.
сн
теор статики (теорема Пуансо): Всякую
пространственную систему сил в общем
случае можно заменить эквивалентной
системой, состоящей из одной силы,
приложенной в какой-либо точке тела
(центре приведения) и равной главному
вектору данной системы сил, и одной пары
сил, момент которой равен главному
моменту всех сил относительно выбранного
центра приведения.
