8.3.2. Многошаговые методы решения задачи Коши

В данном случае построение разностных расчетных схем (8.11) основано на том, что для определения y_i+1 используются результаты не одного, а k предыдущих шагов y_i–k+1, y_i–k+2, ..., y_i в данном случае это k шаговый метод.

Многошаговые методы могут быть построены следующим образом. Исходное уравнение (8.4) для задачи Коши запишем в виде dY(x) = f(x, y)dx. Проинтегрируем обе части этого соотношения на отрезке [x_i, x_i+1].

Из левой части получаем

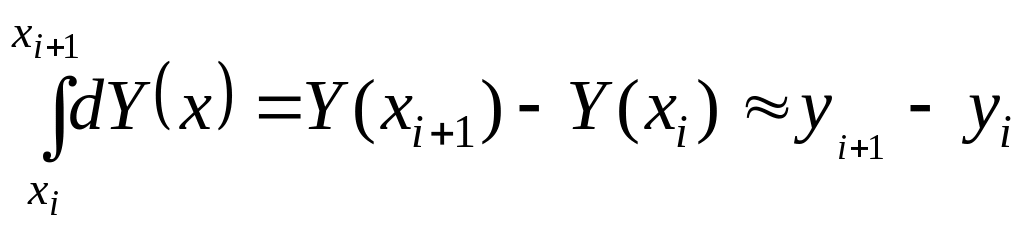, (8.23)

где y_i+1, y_i – сеточные значения искомой функции.

Для вычисления интегралов правой части сначала построим интерполяционный многочлен P_k–1(x) степени (k – 1) для функции f(x, Y) на этом отрезке по значениям f(x_i–k+1, Y_i–k+1), f(x_i–k+2, Y_i–k+2), ..., f(x_i, Y_i). Тогда

. (8.24)

Приравнивая (8.23) и (8.24), получаем формулу для определения неизвестного значения сеточной функции y_i+1 в узле х_i+1:

. (8.25)

На основе (8.25) можно строить различные многошаговые методы любого порядка точности. Порядок точности при этом зависит от степени P_k–1(x), для построения которого используются значения сеточной функции y_i, y_i–1, ..., y_ik+1, вычисленные на k предыдущих узлах.

На практике широко используются следующие многошаговые методы.

Семейство методов Адамса. Известны методы Адамса k-го порядка. Простейший из них при k = 1 повторяет метод Эйлера первого порядка в точности. Метод четвертого порядка на практике принято называть методом Адамса. Рабочую формулу для него получают следующим образом.

Пусть известные в четырех последовательных узлах (k = 4) значение сеточной функции y_i–3, y_i–2, y_i–1, y_i и вычисленные первоначально значения правой части (8.4) f_i–3, f_i–2, f_i–1, f_i. В качестве интерполяционного многочлена P₃(x) возьмем многочлен Ньютона. В случае h = const конечные разности для правой части в узле x_i будут иметь вид

f_i = f_i – f_i–1;

²f_i = f_i – 2 f_i–1 + f_i–2;

³f_i = f_i – 3 f_i–1 + 3 f_i–2 – f_i–3.

Тогда разностная схема метода Адамса запишется в виде

. (8.26)

По сравнению с методом Рунге  Кутта той же точности можно отметить его экономичность, так как (8.26) предусматривает на каждом шаге только один раз вычисление правой части в соотношении (8.4). Однако расчет здесь можно начать только с узла x₄. Значения y₁, y₂, y₃, необходимые для вычисления y₄, нужно определять одношаговым методом, что несколько усложняет алгоритм вычисления. Кроме того, метод Адамса не позволяет изменять шаг h в процессе счета, что доступно для одношаговых методов.

Многошаговые методы, использующие неявные разностные схемы. На практике они называются методами прогноза и коррекции или (методами предиктор  корректор).

Их суть состоит в том, что на каждом шаге расчета вводятся два этапа, использующие многошаговые методы:

а) с помощью явного метода (предиктора) по известным значениям функции в предыдущих узлах находится начальное значение y_i+1 = в новом узле;

б) используя неявный метод (корректор) в результате итераций находятся приближения , ... . Посредством корректора итерации продолжаются до тех пор, пока и не совпадут по желаемой точности, затем осуществляется переход к следующей точке сетки, т. е. по рассмотренному выше алгоритму определяется значение y_i+2. Одним из вариантов метода прогноза и коррекции является метод на основе метода Адамса четвертого порядка.

Вид разностных соотношений на этапе предиктора:

; (8.27)

на этапе корректора:

. (8.28)

В (8.27) и (8.28) используются не f_i (конечные разности), а значения правой части (8.4), что удобнее для реализации на ПК. Явная схема (8.27) используется на каждом шаге лишь один раз, а с помощью неявной схемы (8.28) строится итерационный процесс вычислений y_i+1, поскольку это значение входит в правую часть выражения f_i+1 = f(x_i+1, y_i+1).

В данных формулах, как и в случае метода Адамса, при вычислении y_i+1 необходимы значения сеточной функции в четырех предыдущих узлах: y_i–3, y_i–2, y_i–1, y_i. Расчет по этому методу может быть начат только со значения y₄.

Необходимые при этом значения y₁, y₂ и y₃ находятся по методу Рунге  Кутта, y₀ задается начальным условием.

Метод Адамса легко распространяется на системы дифференциальных уравнений.

Повышение точности результатов. Точность можно повысить путем уменьшения значения шага h. Но этот путь ограничен требованием экономичности, поскольку это может потребовать огромного объема вычислений.

На практике часто для повышения точности численного решения без существенного увеличения машинного времени используется метод Рунге. Его суть состоит в том, что по одной и той же разностной схеме проводятся повторные расчеты с различными шагами. В соответствие с методом Рунге уточненное значение сеточной функции в узлах сетки с шагом h вычисляется по формуле .

Порядок точности этого решения равен (k + 1), хотя используемая разностная схема имеет порядок точности k, т. е. точность повышается на порядок.