7. Численное дифференцирование

7.1. Постановка задачи

К численному дифференцированию (ЧД) прибегают тогда, когда приходится вычислять производные для функций, заданных таблично, или когда непосредственное дифференцирование y = f(x) затруднительно. Формулы для расчета в точке x области определения функции получают посредством аппроксимации оператора дифференцирования интерполяционными многочленами как локальной, так и глобальной интерполяции. А именно, берутся несколько близких к исследуемой точке x узлов x₁, x₂,…, x_n (n  m + 1), называемых шаблоном. Вычисляются значения y_i = f(x_i) в узлах шаблона, и строится интерполяционный многочлен

.

Тогда .

Для получения рабочих формул численного дифференцирования с точки зрения упрощения их реализации интерполирование производится на равномерной сетке, и производные обычно находятся в узлах x_i с соответствующей оценкой их погрешностей. При n = m + 1 формулы ЧД не зависят от положения точки x внутри шаблона, так как m-я производная от полинома m-й степени есть константа. Такие формулы называются простейшими формулами ЧД.

7.2. Аппроксимация производных посредством локальной интерполяции

В случае табличного задания функции производную находят, опираясь на формулу

,

полагая

. (7.1)

Это соотношение называется аппроксимацией производной с помощью отношения конечных разностей. При заданных значениях таблицы {x_i, y_i}, i = и шаге расположения интерполяционных узлов h = const в зависимости от способа вычисления конечных разностей для i-го узла используются различные алгоритмы вычисления (7.1).

Пусть i = 1.

1. Формула левых разностей:

; ;

. (7.2)

2. Формула правых разностей:

; ;

. (7.3)

3. Формула центральных разностей:

; ;

. (7.4)

С помощью соотношений (7.2), (7.3), (7.4) последовательно можно получить выражения для вычисления производных высших порядков. Например, используя (7.3), получим

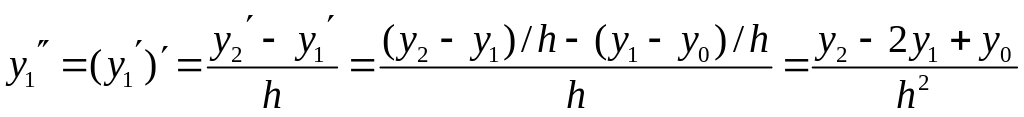. (7.5)

Открытым остается вопрос точности.

7.3. Погрешность численного дифференцирования

Аппроксимируя исследуемую функцию, ее представляют в виде

. (7.6)

В качестве (x) можно принять либо интерполяционную функцию, либо частичную сумму ряда. Тогда погрешность аппроксимации R(x) определяется остаточным членом ряда или P_n–1(x). Дифференцируя (7.6) необходимое число раз, находим:

и т. д.

Тогда погрешность аппроксимации при численном дифференцировании функции, заданной таблицей с шагом h, зависит от h, и ее записывают в виде О(h^k). Показатель степени k называют порядком погрешности аппроксимации производной. При этом предполагается, что |h| < 1.

Оценку погрешности формул (7.2) – (7.5) можно проиллюстрировать с помощью ряда Тейлора.

Пусть дважды непрерывно дифференцируемая функция f(x) задана таблицей значений:

x	x0	x1	x2	…	xn
y	y0	y1	y2	…	yn

В таблице y_i = f(x_i), i = . Пусть далее используются равностоящие узлы, h = (x_n – x₀)/n, x_i = x₀ + ih, h = x_i+1 – x_i, .

Запишем ряд Тейлора в общем виде:

. (7.7)

Запишем (7.7) при x = x₁, с точностью до h¹:

y₀ = y₁ – y'₁h + O(h²).

Тогда .

Это выражение совпадает с (7.2) и является аппроксимацией первого порядка (k = 1). Тогда для произвольного узла .

По всему отрезку [a, b], где h = (b  a)/n, для f '(x) погрешность не превысит величины R = .

Полагая для (7.7) x = h, можно получить этот результат и для соотношения (7.3). Для оценки погрешности для (7.4) и (7.5) воспользуемся рядом Тейлора с учетом того, что x = –h и x = h. Соответственно получим

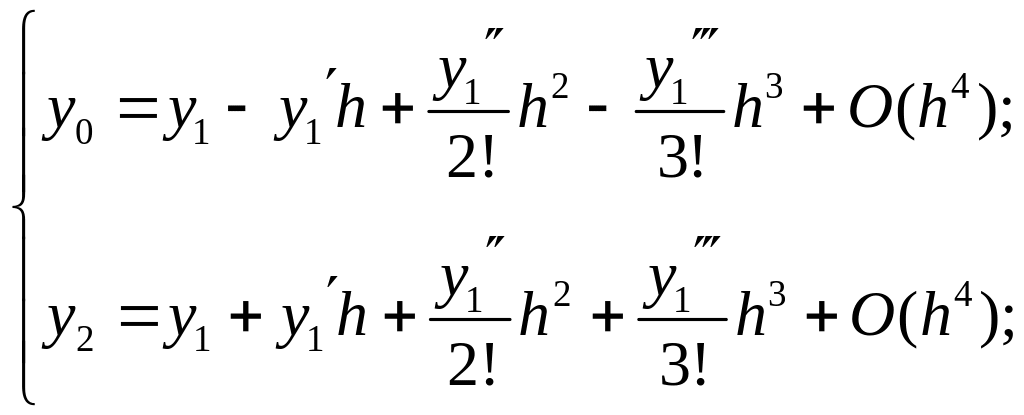(7.8)

в предположении, что f(x) трижды непрерывно дифференцируемая функция.

Вычитая из второго равенства первое, получаем

+ О(h²), здесь k = 2.

Для произвольного узла

.

На основании (7.7) по всему отрезку погрешность аппроксимации не превзойдет величины

.

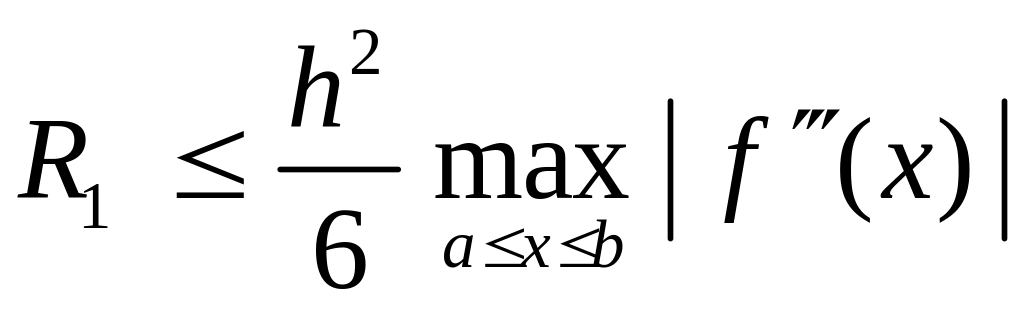Сложив равенства (7.8), найдем

+ О(h²), k = 2.

Для отрезка [x_i–1, x_i+1] получим

, i = .

Погрешность на отрезке [a, b] для второй производной оценивается соотношением

.

Следует отметить, что в целом приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Считают, что при численном дифференцировании функции y = f(x), заданной таблично, имеют место два типа погрешностей:

а) погрешности усечения, которые вызываются заменой функции y = f(x) интерполяционным многочленом P_n(x);

б) погрешности округления, которые вызываются неточным заданием исходных значений y_i.

При этом известно, что с уменьшением шага численного дифференцирования погрешность округления возрастает, а погрешность же усечения, как правило, убывает. Поэтому при вычислениях по формулам численного дифференцирования стоит задача и оптимального выбора шага h.