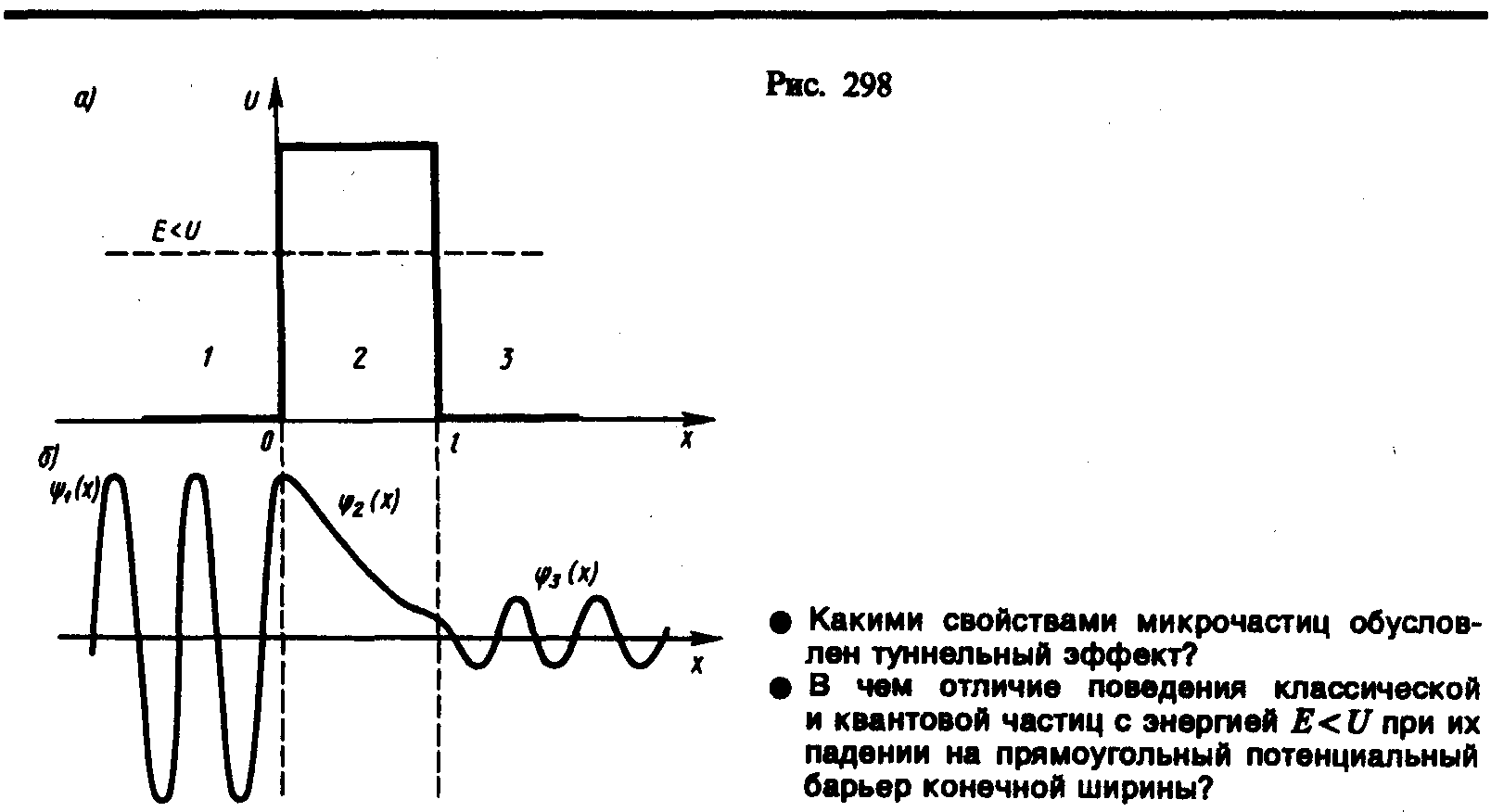
30.Туннельный эффект. Расмм. Потенциальный барьер (пц) прямоугольной формы для одномерного (по оси х) движения частицы.

Класс. частица либо пройдет над барьером (при Е>U), либо отразится от него (при Е<U) движение в обратную сторону, (не может проникнуть сквозь барьер). Для микрочастицы , при Е>U, есть вер-сть, что частица отразится от барьера – движение в обратную сторону. При E<U аналогично. Выводы следуют из решения ур-ния Шредингера.

Ур-ние Шр.для стационарных состояний для каждой

Общие решения этих дифференциальных уравнений:

Для области 1 полная волновая функция:

В выражении первый член - плоская волна, движущ. в полож. направлении оси х (в сторону барьера), а второй — волну, в проти­воположном направлении, (отраженную от барьера).

Решение содержит также волны (после умножения на временной множи­тель), движ. в обе стороны. Однако в области 3 только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэфф. B₃ в ф-ле следует принять = 0.

В обл. 2 при Е<U q=i — мнимое число, где Значения q и B₃=0 ур-ние Шр:

В области 2 функция уже не соответствует плоским волнам, распространя­ющимся в обе стороны, т.к. показатели степени экспонент не мнимые, а дейст­вительные. Сл-но, частица имеет вер-ть пройти через барьер. Туннельного эффекта (микрообъект может «пройти» сквозь ПЦ при E<U).

Для описания ТЭ используют понятие коэффициента прозрач­ности D ПЦ, (отношение плотности потока прошедших частиц к плотности потока падающих). Чтобы найти отношение |А₃/А₁|², нужно условие непрерывности  и ' на границах барьера х=0 и х=l

Можно выразить коэф. A₂, A₃, В₁ и В₂ через А₁. Решение ур-ний для прямоугольного ПЦ дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀ — постоянный множитель(=1) . D зависит от т ,l (U—E); чем шире барьер, тем меньше вер-ть прохождения сквозь него .

Для ПЦ произвольной формы

где U=U(x).

С класс. точки зрения прохождение частицы сквозь ПЦ при Е<U невозможно, т.к. частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. ТЭ является специ­фическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам класс. механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса р на отрезке х=l составляет p>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (р)²/(2m) может оказаться достаточной, чтобы полная энергия частицы оказалась больше потенциальной.

31.Атом водорода в квантовой механике. Состояние эл-на в атоме водорода описывается волновой функцией , удовлетворяющей стационарному ур-нию Шредингера , потенциальная энергия (дв-ие эл-на в кулоновском поле ядра), т — масса эл-на, Е — полная энергия эл-на в атоме. Физ. Смысл:

1. Энергия. В теории дифференциальных уравнений доказывается, что уравнения имеют решения, удовл. требованиям однозначности, конеч­ности и непрерывности волновой функции , только при собственных значениях энергии Сл-но появление дискретных энергетических уровней. нижний уровень Е₁, отвечающий минимальной возможной энер­гии, — основной, остальные (Е_n >Е₁, n = 2, 3, ...) — возбужденные. При Е<0 движение эл-на является связанным — он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n= E_ = 0. При Е>0 движение эл-на является свободным; область непрерывного спектра Е>0 (заштри­хована на рис.) соответствует ионизованному атому. Энергия ионизации атома водорода равна

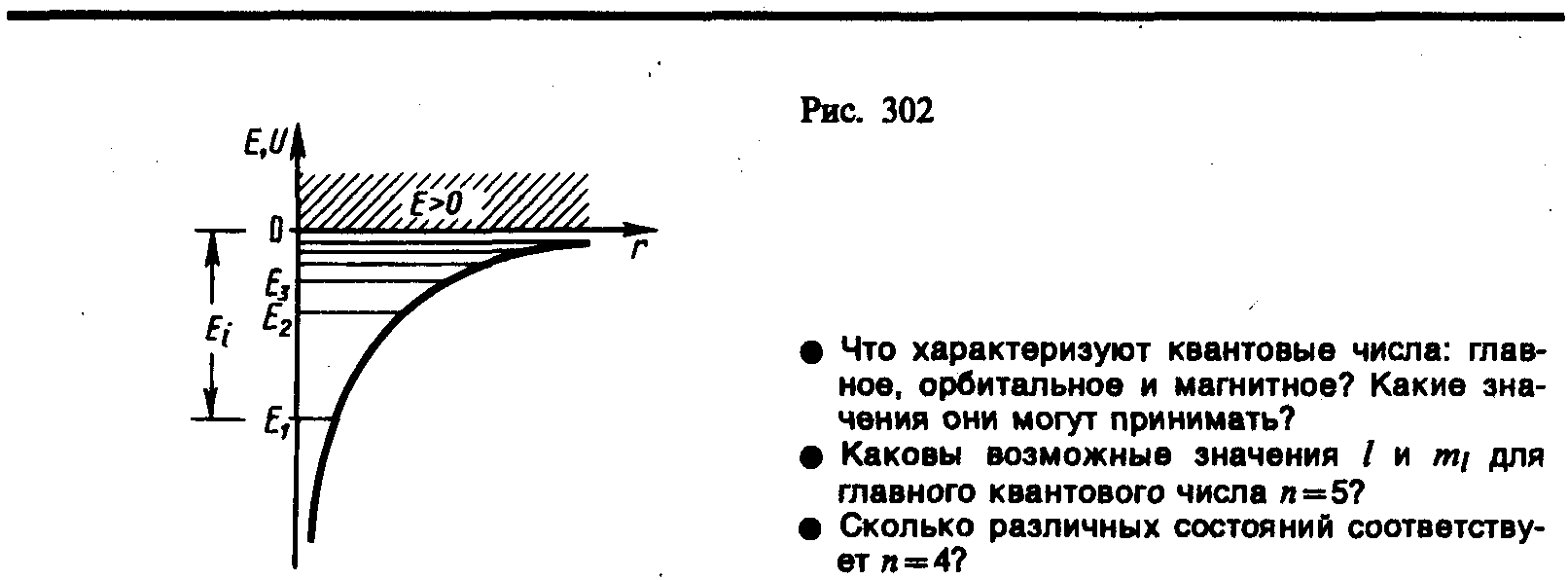
2. Квантовые числа. ур Шр. определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным т_l.

Главное квантовое число n определяет энергетические уровни эл-на, n=1,2,3..Из решения ур Шр - момент импульса (механический орбитальный момент) эл-на квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой где l — орбитальное квантовое число, которое при заданном n принимает значения l=0,1…,n-1.n определяет момент импульса эл-на в атоме.

Из решения ур Шр следует - вектор L_l момента импульса эл-на может иметь лишь такие ориентации в пространстве, при которых его проекция L_lx на направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:

где т_l — магнитное квантовое число, которое при заданном l может принимать значения

Сл-но, магнитное квантовое число m_l определяет проекцию момента импульса эл-на на заданное направление, причем вектор момента импульса эл-на в атоме может иметь в пространстве 2l+1 ориентации.

3. Спектр. Квантовые числа n, l и m_l позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора. Вводятся правила отбора, ограничивающие число возможных переходов эл-ов в атоме, связанных с испусканием и поглощением света. Для дипольного излучения эл-на могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа l удовл. условию 2) изменение магнитного квантового числа m_l удовл. условию