27. Волновая функция и ее статистический смысл

Немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется амплитуда вероятности Y(х, у, z, t) (вер. Обнаружить микрочастицу в пространстве). Y(х, у, z, t) - волновой функцией. Вер. W равна

(|Y|²=YY*, Y* — функция, комплексно сопряженная с Y). След-но, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероят­ностный характер : квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент вр. t в области с корд. х и x+dx, у и y+dy, z и z+dz.

Волновой функция, является основным носителем информации об корпускулярных и волновых св-вах. Вер. нахождения частицы в элементе объемом dV равна Величина имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с коор­. х, у, z. Физ. смысл имеет не сама Y-функция, а квадрат ее модуля |Y|², которым задается интенсивность волн де Бройля.

Вер. найти частицу в момент вр. t в конечном объеме V,

Т.к. |Y|²dV определяется как вероятность, то необходимо волновую функцию Y нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Значит, что частица должна находиться где-то в пространстве. След-но, условие нормировки вероятностей Это говорит об объективном существовании частицы в прост-ве.

Чтобы волновая функция являлась объективной характеристикой состояния микро­частиц, она должна удовлетворять ряду ограничительных условий. Функция Y, харак­теризующая вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком). Волновая функция удовл. принципу суперпозиции: если система может нахо­диться в различных состояниях, описываемых волновыми функциями Y₁, Y₂,..., Y_n,... то она также может находиться в состоянии Y, описываемом линейной комбинацией этих функций:

где С_n (n=1, 2, ...)—произвольные, вообще говоря, комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей отличает квантовую теорию от класс. статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей. Волновая функция Y позволяет в квантовой механике вычислять средние значения физ. величин, харак-щих данный микрообъект. Н-ер, среднее расстояние árñ эл-на от ядра вычисляют по ф-ле

26. Соотношение неопределенностей

В класс. механике частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микроча­стицы из-за наличия у них волновых св-в существенно отличаются от класс. частиц. Различия: нельзя говорить о движе­нии микрочастицы по определенной траектории и неправомерно говорить об одновре­менных точных значениях ее коор. и имп. Это следует из корпускулярно-волнового дуализма.. Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определен­ную координату (х, у, z), и определенную соотв. проекцию имп.(р_х, p_у, p_z).Условие т. е. произведение неопределенностей корд. и соотв. ей проекции имп. не может быть меньше величины порядка h. Например, если микроча­стица находится в состоянии с точным значением координаты (Dx = 0), то в этом состоянии соотв. проекция ее имп. оказывается совершенно неопреде­ленной (Dp_x ® ¥), и наоборот. Для микрочастицы не существует состояний, в кот ее коорд и имп. имели бы одновременно точные значения.

Т.к. в класс. механике принимается, что измерение коор и имп может быть произведено с любой точностью, то соотношение неопределенностей является квантовым ограничением применимости класс. механики к микрообъектам.

Движение по траектории хар-ся опред. значениями корд. и скорости. С.Н в виде

Следует, что чем больше масса частицы, тем меньше неопределен­ности ее коор. и ск-ти и с большей точностью можно применять к этой частице понятие траектории. Например, пыинка массой 10^–12 кг и линейными размерами 10^–6 м, коор. определена с точ­ностью до 0,01 ее размеров (Dх = 10^–8 м), неопределенность ск-ти, Dv_x = 6,62×10^–34/(10^–8×10^–12) м/с = 6,62×10^–14 м/с, т. е. не будет сказываться при всех скоростях, с кот пылинка может двигаться. (Для описания движения макротел можно пользоваться законами класс. механики.)

Например, пучок эл-ов движется вдоль оси х со v=10⁸ м/с, опред. с точностью до 0,01% (Dv_x»10⁴ м/с).

т. е. положение эл-на м.б. определено с точностью до тысячных долей миллиметра. (описывать их движение законами классической механики.)

На-ер, эл-н, движ. в атоме водорода. Коор эл-на Dx»10^–10 м. Тогда Dv_x=6,62×10^–34/(9,11×10^–31 ×10^–10) = 7,27×10⁶ м/с. Используя законы класс. физики, что при движении эл-на вокруг ядра его скорость v » 2,3×10⁶ м/с. 7,27×10⁶ >>2,3×10⁶ м/с ( нельзя пользоваться з-ми класс. физики.)

С.Н. для энергии Е и времени t, улосвие: DЕ — неоп-ь энергии некоторого состояния системы, Dt — промежуток вр, в течение кот оно существует. Систе­ма, имеющая среднее время жизни Dt, не м.б. охарактеризована определенным значением энергии; разброс энергии DE=h/Dt возрастает с уменьшением ср. вр. жизни. Частота излученного фотона должна иметь неоп-ть Dn = DE/h, т. е. линии спектра должны харак-ся частотой, равной n ± DE/h..Опыт действительно показывает, что все спектраль­ные линии размыты; -

28.Уравнение Шредингера. где ћ=h/(2), т—масса частицы, —оператор Лапласа i — мнимая единица, U (х, у, z, t) — потенциальная ф-ция частицы в силовом поле, (х, у, z, t) — искомая волновая ф-ция частицы.

Ур-ние справедливо для любой частицы движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью v<<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волно­вая ф-ция д.б. конечной, однозначной и непрерывной 2) производные должны быть непрерывны; 3) ф-ция ||² д.б. интегрируема; это условие сводится к условию нормировки вероятностей

Чтобы прийти к уравнению Шредингера, рассм. свободно движущуюся частицу, кото­рой, согласно идее де Бройля, сопоставляется плоская волна.. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид , или в комплексной записи . Сл-но, плоская волна де Бройля имеет вид ( = E/ћ, k=p/ћ). В квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет только ||², то это несущественно. Тогда откуда Используя взаимосвязь между энергией Е и импульсом р (E=p²/(2m)) и подставляя выражения получим дифференциальное ур-ние которое совпадает с уравнением (№1) для случая U=0. Если частица движется в силовом поле, характеризуемом потенциальной энергией U, то полная энергия Е складывается из кинетической и потенциальной энергий. Е : p²/(2m)=E–U)

Приведенные рассуждения поясняют, как можно прийти к уравнению Шр. Уравнение (№1) является общим уравнением Шредингера. Его также наз. урав. Шр., зависящим от времени. Если силовое поле, в котором частица движется, стационарно, т. е. ф-ция U=U(x, у, z) не зависит от времени и имеет смысл потенциальной энергии. Решение ур-ния Шредингера может быть представлено в виде произведения двух функций, одна из которых есть ф-ция только координат, другая — только времени, причем зависимость от времени выражается множителем , так что где Е — полная энергия частицы, постоянная в случае стационарного поля. Получим После деления на множитель и преобразований придем к ур-нию, определяющему ф-цию :

29. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Проведем анализ решений уравнения Шредингера применительно к ча­стице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида

l — ширина «ямы», а энергия отсчитывается от ее дна

Ур. Шр. для стационарных состояний: По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а сл-но, и волновая функция) за пределами «ямы»= 0. На границах «ямы» (при х=0 и х=1) непрерывная волновая функция должна обращаться в нуль. Сл-но, граничные усло­вия В пределах «ямы» (0  х  l) ур Шр сведется к ур. или где Общее решение дифференциального ур.: Т.к. (0)=0, то В=0. Тогда Условие (l)=A sin kl = 0 выполняется при kl = n, n — целые числа, т. е. надо, чтобы Из выражений следует, что т. е. стационарное ур Шр, описывающее движение частицы в «потен­циальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Сл-но, энергия Е_n частицы в «потенциальной яме» принимает определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n наз. уровнями энергии, а число п, определяющее энергетические уровни частицы, наз. главным квантовым числом. Сл-но, микрочастица в «по­тенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_n, или частица находится в кван­товом состоянии n. Подставив значение k найдем собственные функции:

Постоянную интегрирования А найдем из условия нормировки В рез-те интегрирования

А = , а собственные функции:

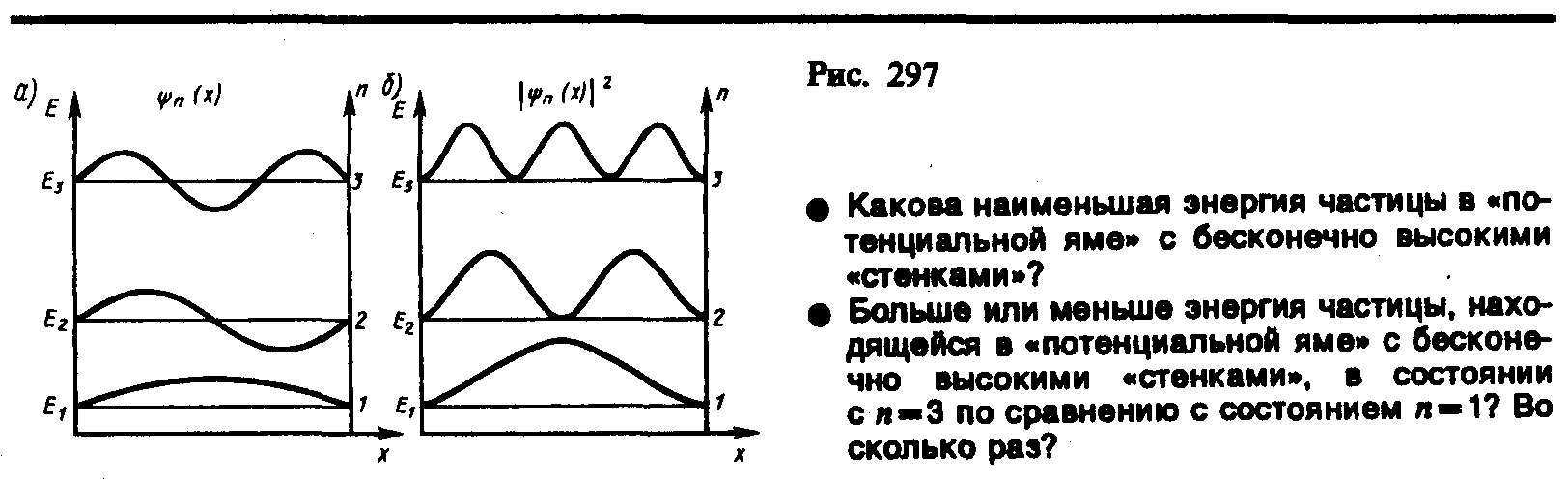
Графики собственных функций , соответствующие уровням энергии при n = 1, 2, 3, приведены на рис. 297,а. На рис. 297,6 изображена плотность вероят­ности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |_n(х)|² = _n(х)*_n(х) для n=1,2 и 3. Из рисунка следует, что в квантовом состоянии с n=2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Это указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны. Энергетический интервал между двумя сосед­ними уровнями равен