
- •Множества. Операции над множествами.
- •Законы алгебры множеств.
- •Мощность множества. Теорема о числе подмножеств конечного множества.
- •Бинарные отношения и их типы
- •Отношение эквивалентности. Теорема о разбиении множества на классы.
- •Перестановки и сочетания
- •Формулы о подсчете числа подстановок из сочетаний с повторениями и без повторений.
- •Высказывания. Операции над высказываниями.
- •Булевы функции
- •12. Законы равносильности. Доказать законы Де Моргана.
- •13. Формулы алгебры логики, их классификация и примеры.
- •14. Алгоритмы определения типа формулы.
- •15. Двойственные формулы. Принцип двойственности.
- •20. Сднф и алгоритмы ее построения.
- •21. Скнф и алгоритмы ее построения.
- •22. Теорема о разложении.
- •23. Контактные схемы.
- •24. Логические схемы.
- •26.Область истенности булевой фун-ции. Покрытие обл. Заданной в днф.
- •27.Метод Блейка,Нельсона, графический метод.
- •28. Минимальная днф. Метод инпликантных матриц.
- •29.Сокращенная днф. Теорема о связи сднф и мднф.
- •30. Тупиковая днф. Теорема о связи тднф и мднф
- •31.Алгоритмпостроения тупиковой днф
- •41. Квантор общности. Теорема о применении квантора общности для предиката определенном на конечном множестве.
- •42. Квантор существования. Теорема о применении квантора существования для предиката определенного на конечном множестве.
- •43. Законы алгебры логики предикатов.
- •44. Тождественно истинные предикаты, примеры. Теорема о тождественно истинных предикатах.
- •45. Тождественно ложные предикаты и теорема о тождественно ложных предикатах.
- •46. Понятие следствия и равносильности предикатов, примеры.
- •47. Формулы алгебры логики предикатов и их классификация.
- •48. Законы Де Моргана для алгебры логики предикатов.
- •49. Закон пронесения квантора общности через конъюнкцию.
- •50. Закон пронесения квантора существования через дизъюнкцию.
- •51.Закон пронесения квантора общности и существования через импликацию.
- •53. Детерминированные функции и графическое изображение (примеры).
- •54. Ограничено-детерминированные функции.
- •55. Диаграммы Мура.
- •56. Канонические уравнения ограничено-детерминированных функций.
- •57. Машины Тьюринга.
- •58. Простейшие функции. Теорема о простейших функциях.
- •59. Операция примитивной рекурсии. Примитивно-рекурсивные функции. Примеры.
- •60. Операция минимизации. Рекурсивные функции.
- •61. Тезисы Тьюринга и Черча. Теорема о связи между рекурсивными функциями и функциями вычислимыми по Тьюрингу (без доказательства).
- •62. Графы. Способы задания графов.
- •63. Формула Эйлера.
- •64. Графы к3,3 и к5,5. Теорема.
- •65. Плоские графы. Теорема о плоских графах (без доказательства).
- •66. Эйлеровые графы. Теорема о Эйлеровых графах. Гамильтоновы графы.
- •67. Деревья. Теорема о деревьях (без доказательства).
- •68. Предмет теории кодирования, алфавитное кодирование.
- •69. Префиксный код. Теорема о префиксном коде.
- •70. Разделимый код. Теорема Маркова (без доказательства).
54. Ограничено-детерминированные функции.
Детерминированная
функция
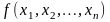 называется ограниченно – детерминированной
функцией, если она имеет конечный вес.
называется ограниченно – детерминированной
функцией, если она имеет конечный вес.
Класс
всех ограниченно
–
детерминированных функций обозначим
через
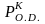
Весом дерева и весом соответствующей детерминированной функции называется максимальное число попарно неэквивалентных поддеревьев.
55. Диаграммы Мура.
Для
любой ограниченно – детерминированной
функции соответствующее ей полное
нагруженное дерево можно свести к
конечному дереву с занумерованными
ребрами и вершинами. Если в нем провести
отождествление эквивалентных вершин,
то получим так называемую диаграмму
Мура. В ней нулём отмечена начальная
вершина и ребрам приписаны пары чисел
(a,
b),
первое из которых обозначает номер
ребра, а второе, чем данное ребро
нагружено. Так функция
 соответствует диаграмме Мура.
соответствует диаграмме Мура.
![]() А
функция
А
функция
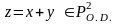
![]()
56. Канонические уравнения ограничено-детерминированных функций.
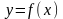 – ограниченно-детерминированная
функция с весом r.
– ограниченно-детерминированная
функция с весом r.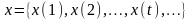 – входная последовательность. Ей
соответствует выходная последовательность
– входная последовательность. Ей
соответствует выходная последовательность и последовательность состояний
и последовательность состояний
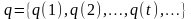 .
.
Возьмем
другую входную последовательность
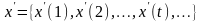 .
.
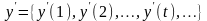 ;
;
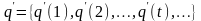 .
.
В
общем случае из того, что
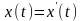 не следует, что
не следует, что
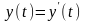 .
Однако, если
и
.
Однако, если
и
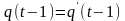 ,
то
и
,
то
и
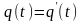 .
Другими словами это означает, что если
два одноименных ребра (
)
выходят из эквивалентных вершин (
),
то они будут нагружены одной и той же
буквой (
)
и будут входить в эквивалентные вершины
(
).
Это означает, что
.
Другими словами это означает, что если
два одноименных ребра (
)
выходят из эквивалентных вершин (
),
то они будут нагружены одной и той же
буквой (
)
и будут входить в эквивалентные вершины
(
).
Это означает, что
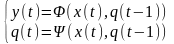
Уравнения называются каноническими уравнениями функции . Первое уравнение называется уравнением выход, второе уравнением перехода.
57. Машины Тьюринга.
Машина Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки. Лента разбита на ячейки. Каждая ячейка находится в одном из двух состояний 0 – пустая; 1. В каждый момент времени лента содержит конечное число ячеек, но в процессе работы машины можно пристраивать новые ячейки в пустом состоянии. Управляющее устройство в каждый момент времени находит в некотором состоянии qi, принадлежащее множеству Q{q0,q1,…,qr-1}, r 1. Множество Q называется внутренним алфавитом. В дальнейшем начальное состояние будем обозначать символом q1, а заключительное символом q0 .
Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита.
Работа машины Тьюринга определяется программой. Программа состоит из команд. Каждая команда представляет собой выражение одного из следующего вида:
qi aj →qk ae;
qi aj →qk ae R;
qi aj →qk ae L.
58. Простейшие функции. Теорема о простейших функциях.
Следующие числовые функции мы будем называть простейшими:
1) O(x) = 0 – нуль-функция
2)
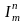 (x1,
x2,…,
xn)
= xm
, 1 ≤ m
≤ n
– функция
повторяющая
значение своих аргументов;
(x1,
x2,…,
xn)
= xm
, 1 ≤ m
≤ n
– функция
повторяющая
значение своих аргументов;
3) S(x) = x+1 – функция следования.
Будем говорить, что n – местная функция φ получается из m – местной функции ψ и n – местных функций f1,f2,…,fm с помощью операции суперпозиции, если для всех x1,x2,…,xn справедливо равенство:
φ (x1,x2,…,xn) = ψ( f1(x1, x2,…, xn),…, fm(x1, x2,…, xn))
