
- •Множества. Операции над множествами.
- •Законы алгебры множеств.
- •Мощность множества. Теорема о числе подмножеств конечного множества.
- •Бинарные отношения и их типы
- •Отношение эквивалентности. Теорема о разбиении множества на классы.
- •Перестановки и сочетания
- •Формулы о подсчете числа подстановок из сочетаний с повторениями и без повторений.
- •Высказывания. Операции над высказываниями.
- •Булевы функции
- •12. Законы равносильности. Доказать законы Де Моргана.
- •13. Формулы алгебры логики, их классификация и примеры.
- •14. Алгоритмы определения типа формулы.
- •15. Двойственные формулы. Принцип двойственности.
- •20. Сднф и алгоритмы ее построения.
- •21. Скнф и алгоритмы ее построения.
- •22. Теорема о разложении.
- •23. Контактные схемы.
- •24. Логические схемы.
- •26.Область истенности булевой фун-ции. Покрытие обл. Заданной в днф.
- •27.Метод Блейка,Нельсона, графический метод.
- •28. Минимальная днф. Метод инпликантных матриц.
- •29.Сокращенная днф. Теорема о связи сднф и мднф.
- •30. Тупиковая днф. Теорема о связи тднф и мднф
- •31.Алгоритмпостроения тупиковой днф
- •41. Квантор общности. Теорема о применении квантора общности для предиката определенном на конечном множестве.
- •42. Квантор существования. Теорема о применении квантора существования для предиката определенного на конечном множестве.
- •43. Законы алгебры логики предикатов.
- •44. Тождественно истинные предикаты, примеры. Теорема о тождественно истинных предикатах.
- •45. Тождественно ложные предикаты и теорема о тождественно ложных предикатах.
- •46. Понятие следствия и равносильности предикатов, примеры.
- •47. Формулы алгебры логики предикатов и их классификация.
- •48. Законы Де Моргана для алгебры логики предикатов.
- •49. Закон пронесения квантора общности через конъюнкцию.
- •50. Закон пронесения квантора существования через дизъюнкцию.
- •51.Закон пронесения квантора общности и существования через импликацию.
- •53. Детерминированные функции и графическое изображение (примеры).
- •54. Ограничено-детерминированные функции.
- •55. Диаграммы Мура.
- •56. Канонические уравнения ограничено-детерминированных функций.
- •57. Машины Тьюринга.
- •58. Простейшие функции. Теорема о простейших функциях.
- •59. Операция примитивной рекурсии. Примитивно-рекурсивные функции. Примеры.
- •60. Операция минимизации. Рекурсивные функции.
- •61. Тезисы Тьюринга и Черча. Теорема о связи между рекурсивными функциями и функциями вычислимыми по Тьюрингу (без доказательства).
- •62. Графы. Способы задания графов.
- •63. Формула Эйлера.
- •64. Графы к3,3 и к5,5. Теорема.
- •65. Плоские графы. Теорема о плоских графах (без доказательства).
- •66. Эйлеровые графы. Теорема о Эйлеровых графах. Гамильтоновы графы.
- •67. Деревья. Теорема о деревьях (без доказательства).
- •68. Предмет теории кодирования, алфавитное кодирование.
- •69. Префиксный код. Теорема о префиксном коде.
- •70. Разделимый код. Теорема Маркова (без доказательства).
48. Законы Де Моргана для алгебры логики предикатов.
Теорема 8 (законы де Моргана для кванторов) Следующие формулы алгебры логики предикатов равносильны:
1)
 ;
;
2)
 ;
;
Доказательство.
1) Пусть А(х)
– произвольный конкретный одноместный
предикат, определённый на произвольном
множестве М.
Тогда
 и
и
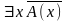 – высказывания.
– высказывания.
Пусть =1. Тогда =0. Отсюда следует, что А(х) 1. А это значит, что 0. Теперь согласно определению 12 =1.
Пусть =0. Тогда =1. Отсюда следует, что А(х) 1. А это значит, что 0. Теперь, согласно определению 12 =0.
Доказательство определения 2) приводится аналогично.
Следствие.
Следующие
формулы алгебры логики предикатов
равносильны:
=

Действительно,
согласно теореме 8 и закону двойного
отрицания получаем
= =
.
=
.
49. Закон пронесения квантора общности через конъюнкцию.
Следующая теорема показывает, что квантор общности можно рассматривать как обобщение конъюнкции.
Теорема 6 Пусть A(x) – одноместный предикат, определенный на конечном множестве M={ a1,a2, … ,an}, тогда = A(a1)·A(a2)·…·A(an).
Доказательство. Пусть = 1, тогда A(x)≡1. Отсюда A(ai)=1 для любого aiM. Но тогда A(a1)·A(a2)·…·A(an)=1. Пусть = 0, тогда
A(x)1. А это значит, что существует ai из M, что A(ai)=0. Но тогда A(a1)·A(a2)·…·A(an)=0. Теорема доказана.
Квантор общности можно применять и к многоместным предикатам. Однократное применение квантора к одной из n переменных n-местного предиката порождает (n-1) – местный предикат.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x > y), определенный на множестве R. Тогда x (x > y) задает одноместный предикат B(y), зависящий от переменной y. Определим тип этого предиката. Возьмем произвольное действительное число y0. Ясно, что
B(y0)= x(x > y0)=0. Следовательно, B(y) – тождественно ложный предикат.
Заметим, что к (n-1)-местному предикату x1 A(x1,x2, … ,xn), зависящему от переменных х1, x2,x3, … ,xn, можно снова применять операцию связывания квантором общности по одной из свободных переменных. В результате получится (n-2)-местный предикат и т.д.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x+y > 2), определенный на R. Тогда xy (x+y > 2) – ложное высказывание, которое читается: «сумма любых двух действительных чисел больше двух».
50. Закон пронесения квантора существования через дизъюнкцию.
Следующая теорема показывает, что квантор существования можно рассматривать как обобщение дизъюнкции.
Теорема 7 Пусть A(x) – одноместный предикат, определенный на конечном множестве M={a1,a2, … ,an}. Тогда x A(x)=A(a1)VA(a2) V…VA(an).
Доказательство. Пусть x A(x)=0. Тогда согласно определению 12 A(x) – тождественно ложный предикат, а значит A(ai)=0 для любого aiM, но тогда A(a1)VA(a2) V…VA(an)=0. Пусть x A(x)=1. Тогда А(х) – не тождественно ложный предикат. А это значит, что найдется значение аi из М, что А(аi)=1. Но тогда А(а1)V А(а2)V…VА(аn)=1. Теорема доказана.
Квантор существования можно применять к многомерным предикатам. Однократное применение квантора к одной из n переменных а-мерного предиката порождает (n-1)-мерный предикат.
Пусть, например, мы имеем двухместный предикат А(х,у)=(х > у) определённый на множестве R. Тогда х(х > y) задает одноместный предикат В(у), зависящий от переменной у. Данный предикат будет тождественно истинным. Действительно, пусть у0 – произвольное фиксированное действительное число. Тогда В(у0)= х(х > y0)=1.
Заметим, что если в многомерном предикате все переменные связаны кванторами, то он будет высказыванием.
Пусть А(х,у)=(х+у > 1) двухместный предикат определённый на множестве R.
Тогда из него связыванием переменных х и у можно получить восемь высказываний:
1 ху(х + у > 2) – “Для всяких действительных чисел х и у их сумма больше двух”.
2 ух(х + у > 2) – “Для всяких действительных чисел у и х их сумма больше двух”.
3 ху(х + у > 2) – “Существуют действительные числа х и у, сумма которых больше двух”.
4 ух(х + у > 2) – “Существуют действительные числа у и х, сумма которых больше двух”.
5 ху(х + у > 2) – “Для всякого действительного числа х существует действительное число у, что их сумма больше двух”.
6 ух(х + у > 2) – “Для всякого действительного числа у существует
действительное число х, что их сумма больше двух”.
7 ху (х+у>2) – “Существует действительное число х, что для всякого действительного числа у их сумма больше двух ”.
8 х (х+у>2) – “Существует действительное число у, что для всякого
действительного числа х их сумма больше двух ”.
Нужно заметить, что высказывания 1 и 2 оба ложны и имеют один и тот же смысл; высказывания 3 и 4 оба истинны и имеют один и тот же смысл. Как видно, изменение порядка одноименных кванторов не влияет на смысл и значение истинности высказывания. Высказывание 5 истинно, а высказывание 8 ложно.
Высказывание 7 ложно, а высказывание 6 истинно. Как видно, изменение порядков разноименных кванторов приводит к изменению смысла и, возможно, значения истинности высказывания.
