61 Стандартизованные коэффициенты регрессии

Стандартизованные коэффициенты регрессии показывают, на сколько % изменится в среднем результат, если соответствующий фактор xi изменится на 1 % при неизменном среднем уровне других факторов.

• Стандартизованные коэффициенты регрессии bi сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат.

• В этом основное стандартизованных коэффициентов регрессии в отличие от коэффициентов “чистой ” регрессии, которые несравнимы между собой.

• коэффициенты “чистой ” регрессии связанны со стандартизованными коэффициентами регрессии следующими формулами :

Это позволяет от уравнения регрессии в стандартизованном виде переходить к уравнению регрессии в естественном виде.

62. Понятие о гомо-и гетероскедастичности остатков. Тесты на гетероскедастичность

Для обнаружения гетероскедастич­ности обычно используют тесты, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда - Квандта, тест Глейзера, двусторонний критерий Фишера и другие. При малом объеме выборки для оценки гетероскедастич­ности может использоваться метод Голдфельда — Квандта. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков воз­растает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая   распределена нормально. Чтобы оценить на­рушение гомоскедастичности по тесту Голдфельда - Квандта необходимо выполнить следующие шаги.

63. Обобщенная линейная модель множественной линейной регрессии. Обобщенный метод мнк

Модель множественной регрессии – решает задачу зависимости одной зависимой переменной (Y) от нескольких объясняющих переменных (X1, X2,…, Xn). Уравнение модели: Yi=f(Xi1, Xi2, …, Xin). Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а так же совокупное воздействие факторов на моделируемый показатель. Построение модели множественной регрессии начинают с решения вопроса о спецификации модели, который включает 2 этапа:

• отбор факторов;

• выбор вида уравнений регрессии.

Индекс множественной корреляции – оценивает тесноту связи по всей совокупности факторов. Индекс множественной детерминации – оценивает качество подбора уравнений регрессии. В обобщенной модели дисперсии объясняющих переменных могут быть произвольными.

64. Взвешенный мнк

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS - Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает "вес", обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: 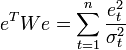 . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.

65. Отбор факторов в модель регрессии. Пошаговые процедуры отбора.

1. Отбор факторов производится на основе качественного теоретико-экономического анализа, то есть включение в уравнение тех или иных факторов должно опираться на понимание природы взаимосвязи экономических переменных.

2. Факторы должны быть количественно измеримы.

3. Каждый из факторов не может быть частью другого

4. Число включаемых факторов должно быть как минимум в 6-7 раз меньше объема совокупности, по которой изучается регрессия

5. Каждый дополнительно включенный в уравнение регрессии фактор должен увеличивать множественный коэффициент детерминации, то есть доля объясненной вариации результативного признака за счет включенного фактора должна увеличиваться, а, соответственно, доля остаточной вариации должна уменьшаться.

6. Факторы, включенные в модель, должны быть независимы друг от друга. Если между самими факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результат и параметры уравнения тогда невозможно интерпретировать.