49.Классификация нелинейных регрессий

Если между эк явлениями сущ нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: н-р, равносторонней параболы у= а+b/х +Е, параболы второй степени у=а+b*х+с*х²+Е

Различают два класса нелинейных регрессий: -регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. –регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции: - полиномы разных степеней: у=а+b*х+с*х²+Е, у=а+b*х+с*х²+d*х³+Е, -равносторонняя гипербола у=а+b/х+Е. К нелинейным регрессиям по оцениваемым параметрам относятся функции: -степенная у=а*х^b*Е, -показательная у=а*b^х*Е, -экспоненциальная у=е ^а+bx*Е

50.Оценка параметров регрессий нелинейных регрессий

Нелинейная регрессия по включенным переменным не имеет никаких сложностей для оценки ее параметров. Они определяются, как и в линейной регрессии, МНК, ибо эти функции линейны по параметрам. Так, в параболе второй степени у=а₀+а₁*х+а₂*х²+Е, заменив переменные х=х₁, х²=х2, получим двухфакторное уравнение линейной регрессии: у=а₀+а₁*х₁+а₂*х₂+Е, для оценки параметров которого используется МНК. Соответственно для полинома третьего порядка у=а₀+а₁*х+а₂*х²+а₃*х³+Е при замене х=х₁, х²=х2, х³=х₃ получим трехфакторную модель линейной регрессии у=а₀+а₁*х₁+а₂*х₂+а₃*х₃+Е,, а для полинома k-го порядка у=а₀+а₁*х₁+а₂*х²+…+а_к*х^к+Е получим линейную модель множественной регрессии с К объясняющими переменными: у=а₀+а₁*х₁+а₂*х₂+…+а_к*х_к+Е. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени, в отдельных случаях-полином третьего порядка. Ограничения в применении полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответсвенно меньше однородность совокупности по результативному признаку. Применение МНК для оценки параметров параболы второй степени у=а+bх+сх²+Е приводит к следующей системе нормальнух уравнений: Σу=n*a+b* Σx+c* Σx²,

Σy*x=a*Σx+b* Σx²+c* Σx³

Σy*x²=a* Σx²+b* Σx³+c* Σx⁴

В классе нелинейных функций, параметры которых без особых затруднений оцениваются МНК, в эконометрике хорошо известна равносторонняя гипербола у=а+b/х. если в уравнении равносторонней гиперболы у=а+ b/х+Е заменить 1/х на z, получим линейное уравнение регрессии у=а+b*z+Е, оценка параметров которого может быть дана МНК. Система нормальных уравнение имеет вид: Σу=n*a+b*Σ1/x

Σу/х=a*Σ1/x+b*Σ1/x²

Во всей этой деятельности существенным является использование моделей. В большинстве случаев экономические законы выражаются в относительно простой математической форме. Рассмотрим, например, функцию потребления

У = А +ВХ₁ + СХ₂

где

У – потребление товара А;

Х₁ – индекс цен на продукцию;

Х₂ – доход на душу населения.

Данная функция описывает в среднем поведение потребителя по отношению к покупке данного товара. Закон поведения будет найден, как только мы найдем значения коэффициентов В и С. Задача эконометрики в этом случае – определить (оценить) эти коэффициенты из подходящего набора наблюдений. Но это не единственная задача, здесь могут возникнуть и другие вопросы:

- нет ли переменных, которые следовало бы дополнительно включить в уравнение (или исключить);

- насколько корректно измерены наши данные (доход, индекс цен). Если они не отражают того, что должны отражать, то поведенческая модель потребителя теряет смысл;

- верно ли, что модель линейна;

- что нужно изучать: макроэкономическое уравнение (данные на уровне областей, регионов) или микроэкономическое ( индивидуальные данные по конкретным людям);

- является модель статической, когда используют данные одного периода, или динамической, поскольку спрос данного года может определяться не только доходом текущего периода, но и прошлых лет?

Эконометрика рассматривает эти и многие другие возникающие вопросы и предлагает способы решения названных проблем.

50.Нелинейная регрессия. Методы линеаризации. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др. Различают два класса нелинейных регрессий: 1)регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; 2)регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: 1)полиномы разных степеней –у = а +bх + с2 + ε, у = а + bх +сх +dx3+ ε; 2)равносторонняя гипербола К нелинейным регрессиям по оцениваемым параметрам относятся функции: 1)степенная — y = axbε; 2) показательная – у = аbх ε; 3)экспоненциальная – y=ea+bxε. Приведение к линейному виду регрессий, нелинейных по объясняющим переменным. Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени у= а0 + а1 х + а2 х2 + ε заменяя переменные х1 =х, х2 = х2, получим двухфакторное уравнение линейной регрессии: у= а0 + а1 х1 + а2 х2 + ε для оценки параметров которого, как будет показано далее, используется МНК. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу Для равносторонней гиперболы такого вида, заменив на z, получим линейное уравнение регрессии y = a +bz +ε оценка параметров которого может быть дана МНК. Она может быть использована не только для характеристики связи удельных расходов сырья,материалов,топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроуровне, но и на макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у. В отдельных случаях может использоваться и нелинейная модель вида так называемая обратная модель, являющаяся разновидностью гиперболы Но, если в равносторонней гиперболе преобразованию подвергается объясняющая переменная z = 1/x и y = а + bz + ε, то для получения линейной формы зависимости в обратной модели преобразовывается у, а именно: z =1/y и z = a + bx +ε. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин 1/у, а именно следовательно полученная методом наименьших квадратов оценка уже не будет эффективной. Приведение к линейному виду регрессий, нелинейных по параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция: y = axbε, где у – спрашиваемое количество; х – цена; ε – случайная ошибка. Данная модель нелинейна относительно оцениваемых пaраметров, ибо включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: lпу = lпа + b lnx + ln ε. Соответственно оценки параметров а и b могут быть найдены МНК. Если же модель представить в виде y = axbε, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. Внутренне нелинейной будет и модель вида — у = а + bхc + ε, ибо это уравнение не может быть преобразовано в уравнение, линейное по коэффициентам. В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель y = еa+bхε, ибо логарифмируя ее по натуральному основанию, получим линейную форму модели: lnу = а + b х +lnε. Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция y = axbε. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия , то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. lпу, 1/у. Так, в степенной функции y = axbε МНК применяется к преобразованному уравнению lпу = lnа + xlnb. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах: .Вследствие этого оценки параметров для линеаризуемых функций МНК оказываются несколько смещенными. При исследовании взаимосвязей среди функций, использующих ln у, в эконометрике преобладают степенные зависимости – это и кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости.

51. Оценка тесноты связи в нелинейной регрессионной модели. Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:                      R=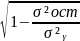   , где σ²ᵧ  - общая дисперсия результативного признака у; σ²_ост – остаточная дисперсия.                                   Величина данного показателя находится в пределах: 0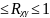 . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака y , объясняемую регрессией, в общей дисперсии результативного признака: Коэффициент детерминации вычисляется по формуле:R²ᵪᵧ =   , где 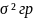   - межгрупповая дисперсия; 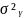- общая дисперсия. Индекс детерминации Rᵪᵧ² можно сравнивать с коэффициентом детерминации  для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина  меньше . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.Индекс детерминации используется для проверки существенности в целом уравнения регрессии по -критерию Фишера: , где  – индекс детерминации,  – число наблюдений,  – число параметров при переменной . Фактическое значение -критерия сравнивается с табличным при уровне значимости  и числе степеней свободы  (для остаточной суммы квадратов) и  (для факторной суммы квадратов).О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле

52

53. Когда количество факторов (без учета константы) больше 1-го, то говорят о множественной регрессии. Матричная запись множественной линейной модели регрессионного анализа: Y = Xb + e, где Y - случайный вектор - столбец размерности (n x 1) наблюдаемых значений результативного признака (y1, y2,..., yn); X - матрица размерности [n x (k+1)] наблюдаемых значений аргументов; b - вектор - столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели; e - случайный вектор - столбец размерности (n x 1) ошибок наблюдений (остатков). На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.

56. Оценка значимости множественной регрессии.Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фшера: где D_факт – факторная сумма квадратов на одну степень свободы;D_ост – остаточная сумма квадратов на одну степень свободы;R² – коэффициент (индекс) множественной детерминации;m - число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов);n – число наблюдений.Коэффициент детерминации R² - одна из наиболее эффективных оценок адекватности регрессионной модели, мера качества уравнения регрессии, характеристика его прогностической силы.Коэффициент детерминации (или множественный коэффициент детерминации)  определяется по формуле: где Q – общая сумма квадратов отклонений зависимости переменной от средней, равное Q_e – остаточная сумма квадратов, характеризующая влияние неучтенных факторов, Q_R – сумма квадратов, обусловленная регрессией, Q=Q_R-Q_e С учетом этого, F-критерий можно найти следующим образом:

59. Мультиколлинеарность и методы ее устранения- высокая взаимная коррелированность объясняющих перпеменных – приводит к значительным ошибкам оцениваемых параметров и недостоверности параметров выборочного уравнения регрессии для генеральной совокупности.Возникает при наличии высокой корреляции между независимыми переменными.Методы устранения: 1) Удаление из регрессионных мод лишних факторов. 2) Преобразование факторов при к-ом уменьшается корреляция между ними. 3) Исп-ие в мод регрессии взаимодействия факторов, например, в виде их произведения. 4) Исп-ие метода главных компонент – сокращение числа независимых факторов до наиболее существенно влияющих факторов.Мультиколлинеарность определяется нарушением требования к рангу матрицы - ранг мат­рицы меньше . Матрица оказывается вырожденной.1) анализируют матрицу парных коэффициентов корре­ляции. наличие значений коэффициентов корреляции > 0,75 - 0,80, свидетельствует о наличии мультиколлинеарности.2) Существование тесных линейных статистических связей между объяс­няющими переменными приводит к слабой обусловленности матрицы .3) Важную роль в анализе мультиколлинеарности играет и минимальное собственное число матрицы .4) Мультиколлинеарность есть когда:n некоторые из оценок имеют неправильные знаки или неоправданно большие по аб­солютной величине значения;n небольшое изменение исходных статистических данных приво­дит к существенному изменению оценок коэффициентов мо­дели, вплоть до изменения их знаков;n большинство или даже все оценки коэффициентов регрессии ока­зываются статистически незначимо отличающимися от нуля, а модель в целом является значимой при проверке с помощью статистики.

60. Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная. Частным коэффициентом корреляции между переменными x_i и x_j при фиксированных значениях остальных (р-2) называется выражение: r_ij.1,2..p = -q_ij / корень из(q_iiq_jj),где через q обозначены алгебраические дополнения.В случае трех переменных: r_{ij k} = r_ij – r_ik r_jk / 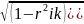.Частные коэффициенты можно найти через остаточные объемы вариации:

R_{ij.1.2…i-1,i+1. j-1,j+1 p} = W_{i1,2…i-1,i+1…j-1,j+1…p} – W_{i1,2 .j…p} / W_{i1,2…i-1,i+1…j-1,j+1…p}, где W_{i1,2 .j…p}-остаточный объем вариации при построении модели регрессии зависимой переменной i от всего набора (р-1) переменных; W_{i1,2…i-1,i+1…j-1,j+1…p}- остаточный объем вариации модели регрессии зависимой переменной I от (р-2) набора переменных (за мсключением j).

В случае трех перменных: r_ijk = W_ik – W_{i jk} / W_ik . Кроме того существует еще один способ расчета:

- в общем виде: r_{ij.1,2…i-1,i+1,j-1,j+1…p} = 1-(1-R²_i1,2…p / 1-R²_{i1,2j-1,j+1.p}).

- в случае трех переменных: r_{ij .k} = 1-(1-R²_ijk / 1-r²_ik).