3. Индуктивно связанные цепи
3.1. Основные положения и определения
При изменении магнитного поля, связанного с каким-либо витком, в последнем наводится ЭДС, которая определяется скоростью изменения магнитного потока, независимо от того, чем вызвано изменение этого потока. В катушке, состоящей из большого числа витков, наводится ЭДС, пропорциональная скорости изменения потокосцепления. Потокосцепление – это сумма магнитных потоков, сцепленных с отдельными витками данной катушки. Если все витки катушки пронизываются одним и тем же магнитным потоком, то потокосцепление равно произведению магнитного потока на число витков.
При рассмотрении цепей гармонического тока мы учитывали лишь явление самоиндукции, т.е. наведение ЭДС в электрической цепи при изменении потокосцепления самоиндукции из-за тока в этой цепи. Отношение потокосцепления самоиндукции к току характеризовалось скалярной величиной – индуктивностью L.
Явление взаимной индукции связано с наведением ЭДС в цепи при изменении потокосцепления взаимной индукции в связи с изменением тока в другой цепи. Такие две электрические цепи называются индуктивно связанными цепями.
Отношение потокосцепления взаимной индукции в одной цепи к току в другой характеризуется взаимной индуктивностью M, которая также является скалярной величиной.
Если потокосцепление W1FM2 первой цепи обусловлено током i2 второй цепи, то взаимная индуктивность цепей определяется как
.
(3.1)
Соответственно потокосцепление W2FМ1 второй цепи, обусловленное током i1 первой цепи характеризуется взаимной индуктивностью
.
(3.2)
Для линейных электрических цепей выполняется равенство M12 = M21. Поэтому индексы у параметра взаимной индуктивности можно упустить.
Справедливость последнего равенства можно доказать, если выразить FM1 и FM2 через соответствующие намагничивающие силы i1W1 и i2W2 и магнитную проводимость путей, по которым замыкаются эти потоки
.
(3.3)
Величина M пропорциональна произведению чисел витков катушек и магнитной проводимости пути общего потока, которая зависит от магнитной проницаемости среды и взаимного расположения катушек.
Свойство взаимности для индуктивно связанных цепей: если ток, проходящий в первой цепи, обусловливает во второй цепи потокосцепление взаимной индукции W2FM1, то такой же ток, проходящий во второй цепи, обусловит в первой цепи потокосцепление взаимной индукции W1FM2 той же величины.
3.2. Полярности индуктивно связанных катушек
Определим ЭДС взаимной индукции.
Положительные направления тока и создаваемого им потока согласуются всегда по правилу правого винта. Условимся, положительные направления токов i1 и i2 в двух индуктивно связанных катушках считать согласными, если положительные направления создаваемых ими магнитных потоков самоиндукции и взаимной индукции совпадают.
На рис. 3.1а, б показано согласное включение двух катушек. Зажимы катушек, относительно которых токи i1 и i2 направлены одинаково, называются одноименными или однополярными. Два одноименных зажима обозначаются точками.
Одноименные зажимы индуктивно связанных катушек характерны тем, что при одинаковом направлении токов i1 и i2 относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции в каждой катушке складываются. Поэтому при вычерчивании электрических схем достаточно наметить на схеме одноименные зажимы индуктивно связанных катушек.
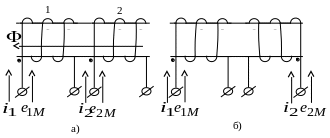
Рис. 3.1. Согласное
включение катушек
ЭДС взаимной индукции при согласном включении
(3.4)
На рис. 3.2а показано согласное, а на рис. 3.2б – встречное включение катушек.
Одноименные зажимы двух индуктивно связанных катушек обладают той особенностью, что подведение к одной из них тока, возрастающего по величине, вызывает возрастание потенциала на одноименном зажиме второй катушки. На этом правиле основан один из методов нахождения одноименных зажимов индуктивно связанных катушек.
Одна из катушек включается в цепь постоянного напряжения, а к другой присоединяется вольтметр постоянного тока. Если в момент замыкания цепи источника стрелка вольтметра отклоняется в сторону положительных показаний, то одноименные зажимы катушек определены верно.
При встречном включении катушек (рис. 3.2б) ЭДС взаимоиндукции равны
(3.5)
Рассмотрим последовательное соединение двух индуктивно связанных катушек (рис. 3.4).
При
согласном направлении токов (рис. 3.4а)
ЭДС взаимной индукции
и
,
совпадающие по направлению с токами,
могут быть заменены падениями напряжения
uM1
= –eM1
и uM2
= –eM2.
Если учесть, что i1
= i2
= i,
то суммарное напряжение цепи будет
.
(3.6)
Две катушки можно заменить одной с активным сопротивлением (R1 + R2) и индуктивностью (L1 + L2 + 2M). Наличие взаимной индукции при согласном включении катушек, соединенных последовательно, увеличивает индуктивность цепи.
При встречном направлении токов
.
(3.7)
Наличие взаимной индукции при встречном включении катушек уменьшает индуктивность цепи.