7. Булевой ф-ией от одного аргумента наз-ся ф-ия , заданная на множестве из двух элементов и принимающая значения в том же двухэлементном мн-ве. : .

Булевой ф-ией от двух аргументов наз-ся ф-ия , заданная на мн-ве и принимающая значения в двухэлементном множестве .Булевой функцией от аргументов наз-ся ф-ия , заданная на мн-ве и принимающая значения в двухэлементном множестве . Другими словами, булева функция от аргументов сопоставляет каждому упорядоченному набору, составленному из элементов 0 и 1, либо 0, либо 1.

Суперпозицией булевых ф-ий в булеву ф-ию наз-ся новая булева ф-ия, получающаяся из ф-ии подстановкой вместо аргументов ф-ий соотв-венно

.

Т.1.Число различных булевых ф-ий от аргументов равно точно .Д-во. Чтобы задать булеву ф-ию от n аргументов, нужно перечислить все наборы из нулей и единиц значений, к-ые могут принимать её аргументы и для каждого такого набора указать значение функции , к-ое она принимает на этом наборе. Выясним сначала, сколько существует различных наборов , составленных из нулей и единиц, значений для аргументов . Покажем, что это число равно . Д-во будем вести методом мат.инд. по числу . В самом деле, для имеется всего два набора значений переменного . Это 0 и 1. Так что для n = 1 число наборов равно 2¹. Предположим, что для аргументов имеется точно различных наборов , составленных из 0 и 1, значений для аргументов. Тогда среди всевозможных различных наборов значений для k + 1 аргумента имеется, согласно предпо­ложению индукции, точно наборов вида и точно 2^к наборов вида . Сл-но, всего будет различных наборов. Тем самым до­казано с помощью индукции утверждение о числе различ­ных наборов.

Т.о., для задания ф-ии от n аргументов нужно указать её значение для каждого из различных наборов значений её аргументов. Если каждое значение функции равно нулю, то такая ф-ия постоянна. Она наз-ся константа 0. Если каждое значение функции равно единице, то это вторая постоянная функция, назы­ваемая константа 1. Мы указали лишь две различные функ­ции от n аргументов. Сколько же их существует всего? Ров­но столько, сколько имеется различных наборов длины , составленных из нулей и единиц. Различных наборов длины , составленных из нулей и единиц, как показано в начале д-ва теоремы, име­ется 2¹, где l = — длина набора. Т.о., число m различных булевых ф-ий от n аргументов равно точно 2¹⁼ .

Система булевых ф-ий наз-ся полной, если всякая булева функция явл-ся суперпозицией ф-ий из этой системы.

Т.2. Следующие системы булевых ф-ий явл-ся полными: 1) ; 2) ; 3) ; 4) ; 5) ; 6) {|}; 7) .

Бу­лева функция принадлежит классу ф-ий , сохраняющих константу 0, тогда и только тогда, когда .

Бу­лева функция наз-ся линейной, её можно представить в виде полинома Жегалкина: , где . Символом обозначим класс всех линейных булевых функ­ций.

Т.3. (Поста: о полноте системы булевых ф-ий). Система булевых ф-ий явл-ся полной тогда и только тогда, когда в этой системе имеется ф-ия, не принадлежащая классу , имеется ф-ия, не принадлежащая классу , имеется ф-ия, не принадлежащая классу S, имеется ф-ия, не принадлежащая классу М, имеется ф-ия, не принадлежащая классу L.

8. Релейно-контактная схема представляет собой физическую систему, построенную из элементов, состоящих из катушки реле и управляемых этой катушкой двух типов контактов, замыкающих и размыкающих. Замыкающие контакты, управляемые i-ой катушкой обозначим через , а размыкающие - через . Всякая РКС может быть представлена как схема с соответствующими соединениями между собой контактов.

Покажем, что любую булеву ф-ию можно представить в виде РКС: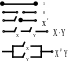

При рассмотрении релейно-контактных схем возникают два типа задач: анализ и синтез, Задача анализа состоит в описании ра­боты схемы. Задача синтеза наоборот по заданному описанию рабо­ты схемы требуется построить соответствующую схему.

9.К первоначальным,

неопределяемым понятиям акс-ской теории выск-ий

относятся след-ие: Х1,Х2,…,Хn-пропозициональные переменные; ¬,→-логические связки; (,) — технические знаки.

Первоначальным понятием явл-ся также понятие ф-лы,

к-ое опр-ся индуктивным образом: 1) каждая пропозициональная переменная есть ф-ла;

2) если F1 и F2 — ф-лы, то выражения ¬F1,(F1→F2)

также явл-ся ф-лами;

3) никаких других формул, кроме получающихся согласно пунктам 1) и 2) нет. След.аксиомы:

(А1)

(А2)

(А3)

Закладывающей основой акс-ой теории выск-ий, состоит в выборе правил

вывода.Единственным правилом вывода будет служить правило

заключения (или отделения, или modus ponens,или сокращенно МР):из формул F и F→G непосредственно следует ф-ла G. Поскольку в аксиомах не участвуют связки , то их

придется определить. Введем следующие определения:

(F G) означает →(F→¬G);

(F G) означает (¬F→G);

(F↔G) означает ((F→G) (G→F)).

Док-вом или выводом формулы F из мн-ва формул Г наз-ся такая конечная посл-сть формул, каждая формула к-ой явл-ся либо аксиомой, либо формулой из Г,либо получена из 2-х предыдущих формул этой посл-сти по правилу modus ponens(МР),а последняя формула совпадает с F. Если имеется вывод формулы F из мн-ва Г, то говорят,что F выводима из Г,или что Г выводит F, и пишут Г├F.Элементы из Г наз-ся гипотезами или посылками вывода.Если же имеется вывод формулы F из пустого мн-ва гипотез, то говорят, что F выводима из аксиом, или что F доказуема, а посл-сть наз-ся док-вом этой формулы.Саму F наз-ют теоремой и пишут├F. Совокупность аксиом, правил вывода и всех теорем,выводимых из аксиом,и представляет собой акс-ую теорию выск-ий, или формализованное исчисление выск-ий.

Т.1.(св-ва выводимости).

а) Если Г├F и Г ∆,то ∆├F; б) Г├F тогда и только тогда, когда в Г сущ-ет такое конечное подмн-во ∆, что ∆├F; в) Если Г├G для любой формулы G из мн-ва ∆ и ∆├F,то Г├F.