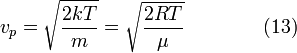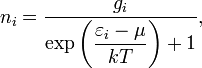30 Среднее число столкновений и средняя длина свободного пробега молекул

Стандартная константа равновесия вещества связана со стандартной энергией Гиббса образования следующим соотношением:

Барометрическая формула

        определяет зависимость давления или плотности газа от высоты в поле тяжести.

         Для идеального газа, имеющего постоянную температуру Т и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), Б. ф. имеет следующий вид:

         р = p₀exp [-gμ.(h - h₀)/RT] (1),

         где р — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), μ — молекулярная масса газа, R — Газовая постоянная, Т — абсолютная температура. Графически зависимость (1) представлена на рис. Из Б. ф. (1) следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

         n =n₀exp [-mg (h-h₀)/kT],

         где m — масса молекулы, k — Больцмана постоянная.

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана: n = n₀exp( -mgh / kT ) где n - концентрация молекул на высоте h, n₀ - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

 Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайноесобытие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина.Случайная величина является одним из центральных понятий теории вер-тей

32 В процессе становления молекулярно-кинетической теории газов некоторое время считалось, что все молекулы газа в условиях термоди-намического равновесия движется с одинаковыми скоростями. Однако движение происходит в разных направлениях, тогда столкновения молекул происходят под различными углами. Это должно приводить к изменению скорости сталкивающихся молекул. Столкновения молекул газа между собой носят случайный характер, следовательно, их скорости должны являться случайными физическими величинами. Область воз можных значений этой физической величины ничем не ограничена, поэтому скорости молекул в газе в условиях термодинамического равновесия – непрерывная случайная величина, для описания которой необходимо построить соответствующую функцию распределения Функция распределения молекул газа по скоростям была выведена Дж. Максвеллом в 1859 г. и носит его имя Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

Наиболее вероятная скорость

наиболее вероятная скорость,   — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  . Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно  :

Средняя кинетическая энергия частиц. df (v) / N = f (v) dv ; Кинетическая энергия одной частицы: E = m0 v / 2 ; v = (корень) 2E / m0 ;

Распределения Больцмана-Максвела. Основное уравнение МКТ и максвелские распределения молекул по скорости были получены предположением, что молекулы равномерно распределены по объему и все направления движения молекул равномерно распределены по объему и все направления движения молекул равновероятны. Такие условия могут быть реализованы только в том случае, если на молекулы не действуют никакие внешние силовые поля. Однако молекулы любого газа в земных условиях находятся в потенциальном гравитационном поле Земли, что приводит к нарушению равномерного распределения молекул по объему. P = pgh — давление в жидкости ; dP = - pgdh — т.к. с увеличением высоты давление уменьшается. распределения Больцмана. Оно описывает распределение частиц по высоте в гравитационном поле, а не только в гравитационном поле Земли. Это распределение приемлемо к частицам, находящимся в состоянии заотического теплового движения.

33 Распределение Гиббса — распределение, определяющее количества частиц в различных квантовых состояниях. Основывается на постулатах статистики:

1. Все доступные микросостояния системы равновероятны.

2. Равновесию соответствует наиболее вероятное распределение (подсистем по состояниям).

3. Вероятность пребывания подсистемы в некотором состоянии определяется только энергией состояния.

Распределение Гиббса представляет наиболее общую и удобную основу для построения равновесной статистической механики.

В статистической механике статистика Бо́зе — Эйнште́йна определяет распределение тождественных частиц с нулевым или целочисленным спином(таковыми являются, например, фотоны и атомы гелия-4) по энергетическим уровням в состоянии термодинамического равновесия.

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам вметалле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией   есть

где

 — среднее число частиц в состоянии  ,

 — энергия состояния  ,

 — кратность вырождения состояния   (число состояний с энергией  ),

 — химический потенциал (который равен энергии Ферми   при абсолютном нуле температуры),

 — постоянная Больцмана,

Т—бсолютная температура

34 Фотонные кристаллы (ФК) представляют собой структуры, характеризующиеся периодическим изменением диэлектрической проницаемости в пространстве. Оптические свойства ФК сильно отличаются от оптических свойств сплошных сред. Распространение излучения внутри фотонного кристалла благодаря периодичности среды становится похожим на движение электрона внутри обычного кристалла под действием периодического потенциала.

Фотонные кристаллы интересны как с фундаментальной точки зрения, так и для многочисленных приложений. На основе фотонных кристаллов создаются и разрабатываются оптические фильтры, волноводы (в частности, в волоконно-оптических линиях связи), устройства, позволяющие осуществлять управление тепловым излучением, на основе фотонных кристаллов были предложены конструкции лазеров с пониженным порогом накачки. Помимо изменения спектров отражения, прохождения и поглощения металло-диэлектрические фотонные кристаллы обладают специфической плотностью фотонных состояний. Измененная плотность состояний может существенным образом влиять на время жизни возбужденного состояния атома или молекулы, помещенных внутрь фотонного кристалла, и, следовательно, менять характер люминесценции. Например, если частота перехода в молекуле-индикаторе, находящейся в фотонном кристалле, попадет в запрещенную зону, то люминесценция на этой частоте будет подавлена.

ФК делятся на три типа: одномерные, двумерные и трехмерные.

Колебания кристаллической решетки Кристаллическая структура – равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, то есть не находится в состоянии статического равновесия.

Колебаниям решетки, согласно квантовой механике, можно сопоставить квазичастицы - фононы. Каждому колебанию соответствует одно состояние фонона с импульсом и энергией .

Энергия колебаний и теплоемкость кристаллической решетки Энергию колебаний и теплоемкость решетки будем рассчитывать для единичного объема кристалла, т. е. положим нормировочный объем равным единице: V = L³ = 1. Чтобы вычислить среднюю энергию колебаний кристаллической решетки, нужно просуммировать среднюю энергию всех типов колебаний (всех состояний фононов)
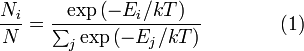