
- •Раздел 8. Свойства электромагнитных волн
- •Раздел 9. Основы квантовой механики
- •Раздел 10. Основы молекулярно-кинетической теории и термодинамики
- •Раздел 11. Второе начало термодинамики. Явления переноса
- •Раздел 12. Элементы квантовой статистики. Физика твердого тела.
- •Раздел 13. Атомное ядро. Элементарные частицы (4часа)
- •30 Среднее число столкновений и средняя длина свободного пробега молекул
- •35 Квантовая теория свободных электронов кристалла.
Раздел 12. Элементы квантовой статистики. Физика твердого тела.
Равновесие идеального газа в поле тяготения. Барометрическая формула. Понятие о функции распределения вероятностей. Распределение Больцмана.
Распределение Максвелла. Распределение частиц по абсолютным значениям скорости. Средняя кинетическая энергия частицы. Распределение Максвелла-Больцмана.
Распределение Гиббса. Распределение Бозе - Эйнштейна и Ферми-Дирака.
Фононный спектр кристаллов. Средняя энергия и теплоемкость колебаний решетки.
Элементы квантовой теории свободных электронов в кристалле. Электронный ферми-газ. Энергия Ферми. Энергетические зоны кристаллической решетки. Заполнение зон: металлы, диэлектрики и полупроводники.
Сверхпроводимость Собственные и примесные полупроводники. Контактные и термоэлектрические явления.
Раздел 13. Атомное ядро. Элементарные частицы (4часа)
Состав и свойства ядер. Ядерное взаимодействие и его обменный характер. Масса и энергия связи в ядре.
Радиоактивные превращения атомных ядер. Закон радиоактивного распада.
Модели ядра. Деление и синтез ядер. Ядерный реактор. Термоядерные реакции.
Элементарные частицы и их классификация.
(1). Плоская электромагнитная волна и ее свойства. Энергия и импульс плоской электромагнитной волны.
Существование электромагнитных волн было предсказано Дж. Максвеллом в1862-1864 г.г Проанализируем бескрайнее трехмерное пространство с декартовой системой координат х, у, z. У которого в каждой точке задана некоторая величина А (её физическая природа безразлична), меняющаяся в пространстве и во времени по закону А = Ao*cos(w*t+-Бетта*z). для волны, распространяющейся в положительном направлении, будем иметь: A+ = Ao*e^-интеграл(бетта*z). в противоположную сторону: A- = Ao*e^+интеграл(бетта*z) Свойства: 1) Поперечность. в плоской электромагнитной волне вектор напряженности электрического поля E, вектор напряженности магнитного поля H и волновой вектор k взаимно перпендикулярны и образуют правовинтовую систему. 2) Синфазность. векторы имеют одинаковые фазы и изменяются синхронно 3) Фазовая скорость - скорость распространения одинаковой фазы. V = (c)/(sqr(эпсиланд * Мю)) 4) Поляризация. Уравнения Максвелла допускают, в частности, такое решение, когда каждый из векторов E и H совершает колебания только вдоль одной из взаимно перпендикулярных осей. Тогда говорят, что волна имеет линейную, или плоскую поляризацию. Плоскость, в которой лежит вектор напряженности электрического поля волны E и волновой вектоор k , называют плоскостью поляризации или плоскостью колебаний. Средняя величина энергии плоской поляризованной волны <W> = eeoA2/2 Дж/см3.
Энергия волны Ев, протекающая через поверхность S , перпендикулярную распространению волны, за время t , равна Ев = <W>cSt. Величину I =<W>c называют интенсивностью. плоская электромагнитная волна с плотностью энергии w имеет импульс Kед в единице объёма, переносимый плоской электромагнитной волной за единицу времени, определяемый по формуле: Kед=w/c.
(2). Естественный и поляризованный свет. Двойное лучепреломление. Закон Малюса.
Естественный свет - это свет, в котором колебания вектора напряженности Е электрического поля происходят по всевозможным направлениям в плоскости, перпендикулярной направлению распространения (к лучу). Плоскополяризованный свет - это свет, в котором колебания вектора Е происходят только в одном направлении, перпендикулярном лучу. Частично поляризованный свет - это свет, в котором колебания в каком-либо направлении ослаблены. Двойное лучепреломление — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o — ordinary), второй же отклоняется в сторону, нарушая обычный закон преломления света, и называется необыкновенным (e — extraordinary). Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла фи между плоскостями поляризации падающего света и поляризатора. I = Ka*Io*cos^2фи
3 Поляриза́ция волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического или магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения
Вращение плоскости поляризации (оптика) — явление, происходящее с лучами поляризованного света, проходящими через некоторые кристаллы, жидкости и пары, находящиеся в естественном состоянии или же под влиянием магнетизма. Световые лучи, исходящие от самосветящихся тел (солнце, пламя свечи или газа и т. п.) по своим физическим свойствам считаются типическими и нормальными. После отражения или преломления нормальные лучи, например солнечные, приобретают некоторые особенности, выступающие особенно отчетливо в случае преломления лучей света в кристаллах, обладающих способностью двойного лучепреломления (см. это слово), каковы, например, кристаллы исландского шпата. Если пропустить солнечный луч сквозь небольшое отверстие, сделанное в непрозрачной пластинке, за которой помещен кристалл исландского шпата, то из кристалла выйдут два луча равной силы света. Солнечный луч разделился, с небольшой потерей силы света, в кристалле на два луча равной световой силы, но по некоторым свойствам отличные от неизмененного солнечного луча и друг от друга. Для определительности в дальнейшем обозначим один из новообразовавшихся лучей буквою O, а другой — буквою E.Происхождение световых лучей приписывают колебательному движению светового эфира (см. Волны света), наполняющего все свободное пространство вселенной и междучастичные промежутки тел. Колебания эфирных частиц в каждом из двух лучей, образовавшихся в исландском шпате, происходят по прямым линиям и такие лучи называются прямолинейно поляризованными (см. Поляризация света). При этом распространение светового луча происходит по направлению, перпендикулярному к направлению колебаний.
4 Когерентные источники света – это источники, которые имеют постоянную во времени разность фаз, согласованное протекание нескольких колебательных или волновых процессов, степень которых различна.
Когерентные волны - волны, характеризующиеся одинаковой частотой и постоянством разности фаз в заданной точке пространства.
Интерференция - это явление наложения когерентных волн - свойственно волнам любой природы (механическим, электромагнитным и т.д.
5 Физическое явление взаимодействия электромагнитной волны с неоднородностями пространства называется дифракцией электромагнитной волны, в частности, дифракцией света. Благодаря дифракции света возникают волны, отражённые от освещаемых объектов, и становится возможным их визуализация. Дифракция световых волн определяет качество оптических приборов, в частности их разрешающую способность. Различают два вида явления дифракции в зависимости от расстояния точки наблюдения до препятствия или неоднородности, а также от вида волнового фронта в точке наблюдения. Если точка наблюдения расположена достаточно далеко от препятствия и в точку наблюдения после взаимодействия с неоднородностью приходит плоская волна, то говорят о дифракции Фраунгофера. В остальных случаях говорят о дифракции Френеля.
ПРИНЦИП ГЮЙГЕНСА: каждый элемент волновой поверхности является источником вторичной сферической волны, а волна в любой точке перед этой поверхностью (с другой стороны от поверхности, нежели реальный источник волны) может быть найдена как результат суперпозиции волн, излучаемых указанными вторичными источниками.
6 Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые жаждой щелью в отдельности, будут одинаковыми.
7 При дифракции Френеля на препятствие падает плоская или сферическая волна, а дифракционная картина наблюдается на экране позади препятствия на конечном расстоянии от него.
При дифракции Френеля на экране получается "дифракционное изображение" препятствия.
Дифра́кция во́лн (лат. буквально разломанный, переломанный, огибание препятствия волнами) явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн.
8 Противоречия классической физики - К началу XX столетия накопился ряд вопросов, на которые в рамках классической физики не удавалось найти ответы. Класси́ческая фи́зика — физика до появления квантовой теории и теории относительности. Основы классической физики были заложены в Эпоху Возрождения рядом учёных, из которых особенно выделяют Ньютона — создателя классической механики.
В трех наиболее важных для человека фазах вещества – газе, жидкости и твердом теле, основу составляют атомы. Стабильность атомов обеспечивается электромагнитным взаимодействием между электронами и атомным ядром, образованным протонами и нейтронами за счет сильного взаимодействия. Ядро является положительно заряженным и занимает область пространства с линейным размером ~10-15 м. Электроны распределены вокруг ядра в области с линейным размером ~10-10 м. Основная масса атома сосредоточена внутри ядра, на электроны приходится <0,05% всей массы. (При плотной упаковке атомных ядер человека массой 100 кг получится область с линейным размером ~5 мкм).
Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.
Гипо́теза
Пла́нка —
гипотеза,
выдвинутая 14 декабря 1900 года Максом
Планком и заключающаяся в том, что при
тепловом излучении энергия испускается
и поглощается не непрерывно, а отдельными
квантами (порциями). Каждая такая
порция-квант имеет энергию , пропорциональной
частоте ν излучения:
![]() .
где h или
.
где h или
![]() — коэффициент пропорциональности,
названный впоследствии постоянной
Планка. На основе этой гипотезы он
предложил теоретический вывод соотношения
между температурой тела и испускаемым
этим телом излучением — формулу Планка.
Позднее
гипотеза Планка была подтверждена
экспериментально.
Выдвижение
этой гипотезы считается моментом
рождения квантовой механики
— коэффициент пропорциональности,
названный впоследствии постоянной
Планка. На основе этой гипотезы он
предложил теоретический вывод соотношения
между температурой тела и испускаемым
этим телом излучением — формулу Планка.
Позднее
гипотеза Планка была подтверждена
экспериментально.
Выдвижение
этой гипотезы считается моментом
рождения квантовой механики
9 Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения (в вакууме) постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
Фотоэффе́кт — это испускание электронов веществом под действием света В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Законы фотоэффекта:
- 1 закон фотоэффекта: количество электронов, вырываемых светом с поверхности металла за единицу времени на данной частоте, прямо пропорционально световому потоку, освещающему металл.
- 2 закон фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
- 3-ий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если , то фотоэффект уже не происходит.
Теоретическое
объяснение этих законов
было дано в 1905 году Эйнштейном. Согласно
ему, электромагнитное излучение
представляет собой поток отдельных
квантов (фотонов) с энергией hν каждый,
где h — постоянная Планка. При фотоэффекте
часть падающего электромагнитного
излучения от поверхности металла
отражается, а часть проникает внутрь
поверхностного слоя металла и там
поглощается. Поглотив фотон, электрон
получает от
него энергию и, совершая работу выхода,
покидает металл:
![]() ,
где
,
где
![]() — максимальная кинетическая энергия,
которую может иметь электрон при вылете
из металла.
— максимальная кинетическая энергия,
которую может иметь электрон при вылете
из металла.
Фотон(от др.-греч. φῶς, род. пад. φωτός, «свет») — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона также равен нулю. Фотон — самая распространённая по численности частица во Вселенной.
Эффект Комптона
— явление
изменения длины волны электромагнитного
излучения вследствие упругого рассеивания
его электронами. Обнаружен американским
физиком Артуром Комптоном в 1923 году для
рентгеновского излучения. При рассеянии
фотона на покоящемся электроне частоты
фотона и (до и после рассеяния
соответственно) связаны соотношением:
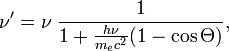
![]()
![]() -
комптоновская
длина волны электрона.
-
комптоновская
длина волны электрона.
10 Корпускуля́рно-волново́й дуали́зм - принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций.
Современная модель атома является развитием планетарной модели. Согласно этой модели, ядро атома состоит из положительно заряженных протонов и не имеющих заряда нейтронов и окружено отрицательно заряженными электронами. Однако представления квантовой механики не позволяют считать, что электроны движутся вокруг ядра по сколько-нибудь определённым траекториям (неопределённость координаты электрона в атоме может быть сравнима с размерами самого атома). Массу атома принято измерять в атомных единицах массы, равных 1⁄12 от массы атома стабильного изотопа углерода 12C
Опыт Франка —
Герца 1913г -
опыт, явившийся экспериментальным
доказательством дискретности внутренней
энергии атома. Опыт Франка — Герца
показал, что спектр поглощаемой атомом
энергии не непрерывен, а дискретен,
минимальная порция (квант электро-магнитного
поля), которую может поглотить атом Hg,
равна 4,9 эВ. Значение длины волны λ =
253,7 нм свечения паров Hg, возникавшее при
V > 4,9 В, оказалось в соответствии со
вторым постулатом Бора.
![]()
В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами. Бройль (1892–1987), французский физик развив идею А. Эйнштейна о двойственной природе, предположил, что поток материальных частиц должен обладать и волновыми свойствами, связанными с их массой и энергией (волны де Бройля).
11 Для описания движения микрочастицы, обладающей волновыми свойствами, не может быть использован способ, разработанный в классической механике, когда состояние частицы определяется заданием в любой момент времени ее пространственных координат и скорости (импульса). При этом движение частицы связано с изменением со временем ее механического состояния, а непрерывная смена состояний соответствует движению частицы по определенной траектории.
Наличие у микрочастицы волновых свойств, как это следует из соотношений неопределенностей Гейзенберга, делает невозможным одновременное точное определение координат и импульса микрочастицы.
12 Вероятность местоположения микрочастицы мы принимаем, что вероятность местонахождения частицы определяется интенсивностью волн, т.е. квадратом амплитуды .Далее следует заметить, что вероятность найти частицу в окрестности точки x,y,z зависит, конечно, от размеров выбираемой области. поэтому вероятность найти частицу следует считать пропорциональной объему этой области… Вывод, при обращении с которым требуется осторожность. …Обозначим этот элемент объема через dv=dxdydz. С точки зрения задание состояния микрочастиц или систем осуществляется заданием волновой функции частицы (или системы).
13 Уравнение Шредингера для стационарных состояний В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение
 где
m - масса частицы,
где
m - масса частицы, ![]() -
мнимая единица, U - потенциальная энергия
частицы, -
оператор Лапласа. Решение уравнения
Шредингера позволяет найти волновую
функцию (x,
y, z, t) частицы, которая описывает
микросостояние частицы и ее волновые
свойства. Частица
в одномерной прямоугольной потенциальной
яме с бесконечно высокими стенками.
Рассмотрение
стационарных задач квантовой механики
начнем с наиболее простой для анализа
задачи - о движении частицы в потенциальной
яме с непроницаемыми, т.е. бесконечно
высокими стенками. Такие ямы называют
еще потенциальными ящиками, наиболее
часто это название применяется по
отношению к трехмерной потенциальной
яме
-
мнимая единица, U - потенциальная энергия
частицы, -
оператор Лапласа. Решение уравнения
Шредингера позволяет найти волновую
функцию (x,
y, z, t) частицы, которая описывает
микросостояние частицы и ее волновые
свойства. Частица
в одномерной прямоугольной потенциальной
яме с бесконечно высокими стенками.
Рассмотрение
стационарных задач квантовой механики
начнем с наиболее простой для анализа
задачи - о движении частицы в потенциальной
яме с непроницаемыми, т.е. бесконечно
высокими стенками. Такие ямы называют
еще потенциальными ящиками, наиболее
часто это название применяется по
отношению к трехмерной потенциальной
яме
Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия
частицы ![]() имеет
вид
имеет
вид
![]()

т.е.
внутри ямы (![]() )
потенциальная энергия
)
потенциальная энергия ![]() постоянна
и равна нулю, а вне ямы обращается в
бесконечность
постоянна
и равна нулю, а вне ямы обращается в
бесконечность
14 Туннельный эффект - туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное и даже полностью противоречащее классической механике. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.
15 Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.
Энергетический уровень - собственные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц) и подчиняющихся законам квантовой механики. Каждый уровень характеризуется определённым состоянием системы, или подмножеством таковых в случае вырождения. Понятие применимо к атомам (электронные уровни), молекулам (различные уровни, соответствующие колебаниям и вращениям), атомным ядрам (внутриядерные энергетические уровни) и т.д.
Главное
(радиальное) квантовое
число — целое
число,
обозначающее номер энергетического
уровня.
Характеризует энергию электронов,
занимающих данный энергетический
уровень.
Является первым в ряду квантовых чисел,
который включает в себя
главное, орбитальное и магнитное квантовые
числа, а также спин.
Эти четыре квантовых числа определяют
уникальное состояние электрона в атоме (его волновую
функцию).
Главное квантовое число обозначается
как ![]() .
При увеличении главного квантового
числа возрастают радиус орбиты и энергия
электрона.Главное квантовое число равно
номеру периода элемента.
.
При увеличении главного квантового
числа возрастают радиус орбиты и энергия
электрона.Главное квантовое число равно
номеру периода элемента.
Орбитальное квантовое число — в квантовой физике квантовое число ℓ, определяющее форму распределения амплитудыволновой функции электрона в атоме, то есть форму электронного облака.
Магни́тное ква́нтовое число́ — параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы).
16
Пространственное
распределение электрона в атоме водорода
Волновое уравнение было предложено
в 1926 г. немецким физиком Э. Шрёдингером
(1887-1961) для описания состояния электрона
в атоме водорода. Он объединил
математические выражения для колебательных
процессов и уравнение де Бройля и получил
следующее линейное дифференциальное
однородное уравнение:

где ψ - волновая функция (аналог амплитуды для волнового движения в классической механике), которая характеризует движение электрона в пространстве как волнообразное возмущение; x, y, z - координаты, m - масса покоя электрона, h - постоянная Планка, E - полная энергия электрона, Ep - потенциальная энергия электрона
17 Сначала заполняем самый низкий энергетический уровень: 1s-орбиталь. На ней размещается 2 электрона. Следующие 2 электрона занимают 2s-орбиталь. Следующий энергетический уровень: 2p-орбиталь - 6 электронов. Следующие 2 электрона - 3s-орбиталь. Оставшиеся 5 электронов располагаются на 3p-орбитали, образуя две спиновые пары (у последнего электрона пары нет).
Электронная конфигурация Все на диаграммах довольно понятно и наглядно, но громоздко. Используя электронную конфигурацию, диаграмму можно выразить одной короткой строкой. Так для хлора: 1s22s22p63s23p5
18 СПИН (ЭЛЕКТРОНА) . Помимо энергии, связанной с движением вокруг ядра атома, электрон обладает еще и дополнительной энергией, связанной с вращением вокруг своей оси наподобие волчка, откуда и происходит слово спин (спин — по-английски верчение). Поскольку же электрон имеет электрический заряд, то при его вращении возникает круговой электрический ток, а следовательно, и магнитное поле, превращающее электрон в маленький электромагнитик, имеющий два магнитных полюса. Так как электрон может вращаться в разных направлениях — по часовой стрелке и против нее, то он может пребывать в двух различных энергетических, или, как говорят, спиновых, состояниях. Спин электрона вызывает ряд дополнительных взаимодействий, играющих исключительно важную роль в физических свойствах атома. Спином обладают и другие элементарные частицы: протон, нейтрон, а также кванты излучений — фотоны. Согласно законам квантовой теории спин имеет строго определенную величину, характерную для данной частицы. В системе единиц, принятой в квантовой теории, спин электрона, а также протона и нейтрона равен 1/2. Спин фотона равен 1.
При́нцип Па́ули (принцип запрета) Распределение электронов в атоме по состояниям.
При́нцип Па́ули — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона (частиц с полуцелым спином) не могут одновременно находиться в одном квантовом состоянии.
Принцип Паули можно сформулировать следующим образом: в пределах одной квантовой системы в данном квантовом состоянии может находиться только одна частица, состояние другой должно отличаться хотя бы одним квантовым числом.
Принцип Паули помогает объяснить разнообразные физические явления. Следствием принципа является наличие электронных оболочек в структуре атома, из чего, в свою очередь, следует разнообразие химических элементов и их соединений. Количество электронов в отдельном атоме равно количеству протонов. Так как электроны являются фермионами, принцип Паули запрещает им принимать одинаковые квантовые состояния. В итоге, все электроны не могут быть в одном квантовом состоянии с наименьшей энергией (для невозбуждённого атома), а заполняют последовательно квантовые состояния с наименьшей суммарной энергией (при этом не стоит забывать, что электроны неразличимы, и нельзя сказать, в каком именно квантовом состоянии находится данный электрон).
Периоди́ческая систе́ма хими́ческих элеме́нтов (табли́ца Менделе́ева) — классификация химических элементов, устанавливающая зависимость различных свойств элементов от заряда атомного ядра. Система является графическим выражением периодического закона, установленного русским химиком Д. И. Менделеевым в 1869 году. Её первоначальный вариант был разработан Д. И. Менделеевым в 1869—1871 годах и устанавливал зависимость свойств элементов от их атомного веса (по-современному, от атомной массы). Всего предложено несколько сотен[1] вариантов изображения периодической системы (аналитических кривых, таблиц, геометрических фигур и т. п.). В современном варианте системы предполагается сведение элементов в двумерную таблицу, в которой каждый столбец (группа) определяет основные физико-химические свойства, а строки представляют собой периоды, в определённой мере подобные друг другу.
19 Спонтанное и вынужденное излучение Вы́нужденное излуче́ние, индуци́рованное излучение — генерация нового фотона при переходе квантовой системы (атома, молекулы, ядра и т. д.) из возбуждённого в стабильное состояние (меньший энергетический уровень) под воздействием индуцирующего фотона, энергия которого была равна разности энергий уровней. Созданный фотон имеет ту же энергию, импульс, фазу и поляризацию, что и индуцирующий фотон (который при этом не поглощается). Оба фотона являются когерентными.
Спонтанное излучение или спонтанное испускание — процесс самопроизвольного испускания электромагнитного излучения квантовыми системами (атомами,молекулами) при их переходе из возбуждённого состояния в стабильное.
Трёхуровневый лазер Классическая трёхуровневая система накачки рабочей среды используется, например, в рубиновом лазере. Рубин представляет собой кристалл корунда Al2O3, легированный небольшим количеством ионов хрома Cr3+, которые и являются источником лазерного излучения. Из-за влияния электрического поля кристаллической решётки корунда внешний энергетический уровень хрома E2 расщеплён (см. эффект Штарка). Именно это делает возможным использование немонохроматического излучения в качестве накачки[9]. При этом атом переходит из основного состояния с энергией E0 в возбуждённое с энергией около E2. В этом состоянии атом может находиться сравнительно недолго (порядка 10−8 с), почти сразу происходит безызлучательный переход на уровень E1, на котором атом может находиться значительно дольше (до 10−3 с), это так называемый метастабильный уровень. Возникает возможность осуществления индуцированного излучения под воздействием других случайных фотонов. Как только атомов, находящихся в метастабильном состоянии становится больше, чем в основном, начинается процесс генерации
=================================== уровень 3, E3, N3
^ |
| | R (быстрый переход без излучения)
| V
--|-------------------------------- уровень 2, E2, N2
| |
| |
| P (накачка) |
| | L (медленный переход с излучением)
| |
| |
| V
----------------------------------- уровень 1 (осн. состояние), E1, N1
20 Термодинамика и статистическая (молекулярная) физика как 2 подхода к описанию макросистем.Молекулярная физика и термодинамика — разделы физики, в которых изучаются свойства тел и происходящие в них макроскопические процессы, связанные с огромным числом частиц, содержащихся в телах. Для исследования этих процессов пользуются двумя методами: молекулярно-кинетическим (статистическим) и термодинамическим. Термодинамика изучает общие свойства тел и различные процессы в них, сопровождающиеся превращениями энергии, на основе двух начал — фундаментальных законов, установленных в результате обобщения огромного числа опытных фактов, не используя какую-либо определенную модель строения вещества и не высказывая предположения о законах взаимодействия атомов и молекул. В термодинамике изучаются тепловые процессы — процессы, связанные с изменением температуры тела, а также с изменением его агрегатного состояния.
Если макроскопические параметры системы имеют одинаковые значения во всем объеме, занимаемом системой, и не изменяются с течением времени, то состояние системы является равновесным. Последовательный переход системы из одного равновесного состояния в другое, совершаемый достаточно медленно, так, что в любой заданный момент времени систему можно характеризовать определенными равновесными значениями термодинамических параметров: давления, температуры или объема, называется равновесным процессом.
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабатасоответственно.
Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
![]()
где
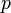 — давление,
— давление,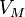 — молярный
объём,
— молярный
объём,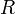 — универсальная
газовая постоянная
— универсальная
газовая постоянная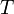 — абсолютная
температура,К.
— абсолютная
температура,К.
21 Первое начало термодинамики — одно из основных положений термодинамики, являющееся, по существу, законом сохранения энергии в применении к термодинамическим процессам.
Первое начало термодинамики было сформулировано в середине XIX века в результате работ Ю. Р. Майера, Джоуля и Г. Гельмгольца. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил.
Первый закон (первое начало) термодинамики можно сформулировать так:
«Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщенного системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале μ, и работы A', совершённой над системой внешними силами и полями, за вычетом работы А, совершённой самой системой против внешних сил» :
ΔU = Q − A + μΔN + A'. Для элементарного количества теплоты δQ, элементарной работы δA и малого приращения (полного дифференциала) dU внутренней энергии первый закон термодинамики имеет вид:
dU = δQ − δA + μdN + δA'. Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая – работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.
Важно заметить, что dU и dN являются полными дифференциалами, а δA и δQ - нет. Приращение теплоты часто выражают через температуру и приращение энтропии: δQ = TdS.
22 Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: где
— подведённая к телу теплота, измеренная в джоулях
[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях
Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
все тела состоят из частиц: атомов, молекул и ионов;
частицы находятся в непрерывном хаотическом движении (тепловом);
частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
![]() ,
,
![]() .
.
Теорема о равнораспределении кинетической энергии по степеням свободы, закон равнораспределения, теорема о равнораспределении — связывает температуру системы с её средней энергией в классической статистической механике. В первоначальном виде теорема утверждала, что при тепловом равновесии энергия разделена одинаково между её различными формами, например, средняя кинетическая энергия поступательного движения молекулы должна равняться средней кинетической энергии её вращательного движения.
С помощью теоремы о равнораспределении можно делать количественные предсказания. Как и вириальная теорема, она даёт полные средние кинетические и потенциальные энергии для системы при данной температуре, из которых можно вычислить теплоёмкость системы. Однако теорема о равнораспределении также позволяет определить средние значения отдельных компонентов энергии, такие как кинетическая энергия одной частицы или потенциальная энергия отдельной пружины. В теореме утверждается, что каждая молекула в идеальном газе обладает средней кинетической энергией равной (3/2)kBT при термодинамическом равновесии, где kB — постоянная Больцмана, T — температура. В общем случае её можно применять к любой классической системе, находящейся в состоянии теплового равновесия, независимо от того, насколько она сложна. Теорема о равнораспределении может использоваться для вывода уравнения состояния идеального газа и закона Дюлонга — Пти, для определения удельной теплоёмкости твёрдых тел. Её также используют в предсказании свойств звёзд, даже таких как белые карлики и нейтронные звезды, поскольку закон равнораспределения остаётся верен даже когда следует учитывать релятивистские эффекты.
23
Теплоемкость системы
Теплоёмкостью системы называется
количество тепла, которое необходимо
сообщить системе, чтобы температура её
увеличилась на 1o. Если под системой
понимается 1 моль вещества, то теплоёмкость
называется молярной и обозначается C.
Если под системой понимается единица
массы вещества, то теплоёмкость называется
удельной и обозначается Суд. Здесь m –
масса; M – молярная масса; Cm – теплоёмкость
системы массы m.
![]()
Внутренняя
энергия Так
как энергия одной молекулы идеального
газа ![]() ,
то внутренняя
энергия одного моля идеального
газа равна:
,
то внутренняя
энергия одного моля идеального
газа равна:
|
|
|
|
то есть
|
|
|
(4.3.1) |
Внутренняя энергия произвольного количества газа:
|
|
|
(4.3.2) |
Её изменение:
|
|
|
|
Теплоемкости многоатомных газов Опыты с двухатомными газами, такими как азот, кислород и др., показали, что
|
|
|
|
Для водяного пара и других многоатомных газов (СН3, СН4 и так далее)
|
|
|
|
Таким образом, молекулы многоатомных газов нельзя рассматривать как материальные точки. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул. Числом степени свободы (i) называется число независимых переменных, определяющих положение тела в пространстве. Положение одноатомной молекулы, как и материальной точки, задаётся тремя координатами, поэтому она имеет три степени свободы (рис. 4.3).
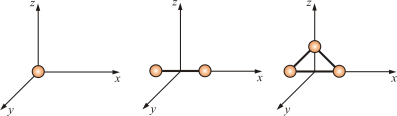 Рис.
4.3
Рис.
4.3
Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомной молекулы вращение вокруг её собственной оси не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю (рис. 4.3). Таким образом, у двухатомных молекул пять степеней свободы (i = 5), а у трёхатомных шесть степеней свободы (i = 6).
При
взаимных столкновениях молекул возможен
обмен их энергиями и превращение энергии
вращательного движения в энергию
поступательного движения и обратно.
Таким путём было установлено равновесие
между значениями средних энергий
поступательного и вращательного движения
молекул. Больцман
доказал,
что
для не слишком низких температур средняя
энергия ![]() ,
приходящаяся на одну степень свободы,
равна
,
приходящаяся на одну степень свободы,
равна ![]()
24 Для любого идеального газа справедливо соотношение Майера:
![]() ,
,
где
— универсальная
газовая постоянная, ![]() —
молярная теплоёмкость при
постоянном давлении,
—
молярная теплоёмкость при
постоянном давлении, ![]() —
молярная теплоёмкость при постоянном
объёме.
—
молярная теплоёмкость при постоянном
объёме.
Адиабати́ческий, или адиаба́тный— термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессыобратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы
. Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает
электростатическое поле,
стационарное поле температуры,
поле давления,
поле потенциала скорости в гидродинамике.
Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.
Это
уравнение имеет вид: ![]()
где ![]() — оператор
Лапласа или лапласиан,
а
— оператор
Лапласа или лапласиан,
а ![]() — вещественная или комплексная функция на
некотором многообразии.
— вещественная или комплексная функция на
некотором многообразии.
В трёхмерной декартовой системе координат уравнение принимает форму:
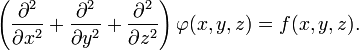
25 Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.
Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:
![]()
где p — давление; V - объем T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.
|
( |
Уравнение Ван-дер Вальса.
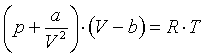
Фа́зовый перехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.
Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.
Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул и из потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ. р΄=а/V2 Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, или, иными словами, против внутреннего давления, как известно из механики, идёт на увеличение потенциальной энергии системы.
26 Энтропия — понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния
Закон возрастания энтропии - Формулировка теоремы
Если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает — увеличивается или в предельном случае остается постоянной.
27 Циклические процессы. Если в ходе термодинамического процесса система возвращается в исходное состояние, то такой процесс называется круговым или циклическим. Круговые процессы, также как и любые другие термодинамические процессы, могут быть как равновесными (а следовательно - обратимыми), так и неравновесными (необратимыми). При обратимом круговом процессе после возвращения термодинамической системы в исходное состояние в окружающих ее телах не возникает никаких термодинамических возмущений, и их состояния остаются равновесными. В этом случае внешние параметры системы после осуществления циклического процесса возвращаются к своим исходным значениям. При необратимом круговом процессе после его завершения окружающие тела переходят в неравновесные состояния и внешние параметры термодинамической системы изменяются. К.П.Д. цикла. Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины, цикла) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой
![]() x
100 %,
x
100 %,
где А — полезная работа, а Q — затраченная работа.
28 Неравенство Клаузиуса (1854): Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено (приведённое количество теплоты), неположительно.
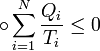
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю. Существуют несколько эквивалентных формулировок второго начала термодинамики:
Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»[1] (такой процесс называется процессом Клаузиуса).
Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).
Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии топлива, тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем. Работа, совершаемая двигателем, равна:
![]() ,
где:
,
где:
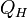 —
количество теплоты,
полученное от нагревателя,
—
количество теплоты,
полученное от нагревателя,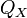 —
количество теплоты,
отданное охладителю.
—
количество теплоты,
отданное охладителю.
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. 29 Уравнение диффузии или уравнение теплопроводности представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
Математически уравнение диффузии и уравнение теплопроводности не различаются, и применение того или иного названия ограничено только конкретным приложением, причем второе представляется более частным, так как можно говорить, что в этом случае речь идет о диффузии тепловой энергии.
В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии. При решении уравнения теплопроводности речь идет о нахождении зависимости температуры среды от пространственных координат и времени, причем задана теплоемкость и теплопроводность среды (также в общем случае неоднородной).
Физи́ческая кине́тика (др.-греч. κίνησις — движение) — микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в различных физических системах (газах, плазме, жидкостях, твёрдых телах) и влияние на них внешних полей. В отличие от термодинамики неравновесных процессов и электродинамики сплошных сред, кинетика исходит из представления о молекулярном строении рассматриваемых сред, что позволяет вычислить из первых принципов кинетические коэффициенты, диэлектрические и магнитные проницаемости и другие характеристики сплошных сред.
