[Править]Цели регрессионного анализа

1. Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами(независимыми переменными)

2. Предсказание значения зависимой переменной с помощью независимой(-ых)

3. Определение вклада отдельных независимых переменных в вариацию зависимой

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.

[Править]Математическое определение регрессии

Строго регрессионную зависимость можно определить следующим образом. Пусть  ,   — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений   определено условное математическое ожидание

 (уравнение линейной регрессии в общем виде),

то функция   называется регрессией величины Y по величинам  , а её график — линией регрессии   по  , или уравнением регрессии.

Зависимость   от   проявляется в изменении средних значений Y при изменении  . Хотя при каждом фиксированном наборе значений   величина   остаётся случайной величиной с определённым рассеянием.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении  , используется средняя величина дисперсии Y при разных наборах значений   (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).

[Править]Метод наименьших квадратов (расчёт коэффициентов)

На практике линия регрессии чаще всего ищется в виде линейной функции  (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых   от их оценок   (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

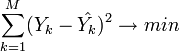
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда  .

Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

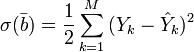
Условие минимума функции невязки:

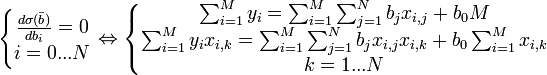
Полученная система является системой   линейных уравнений с   неизвестными 

Если представить свободные члены левой части уравнений матрицей

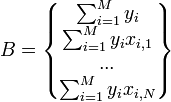
а коэффициенты при неизвестных в правой части матрицей

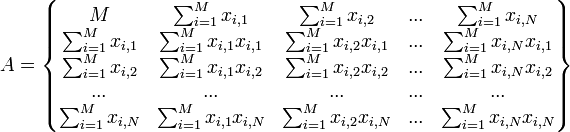
то получаем матричное уравнение:  , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.

[Править]Интерпретация параметров регрессии

Параметры   являются частными коэффициентами корреляции;   интерпретируется как доля дисперсии Y, объяснённая  , при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад   в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.

Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида  ,  , свидетельствующее о наличии взаимодействий между признаками  ,   и т. д (см. Мультиколлинеарность).

Линейная регрессия является статистическим инструментом, используемым для прогнозирования будущих цен исходя из прошлых данных, и обычно применяется, чтобы определить, когда цены являются перегретыми. Используется метод наименьшего квадрата для построения «наиболее подходящей» прямой линии через ряд точек ценовых значений. Ценовыми точками, используемыми в качестве входных данных, может быть любое из следующих значений: открытие, закрытие, максимум, минимум, (максимум+минимум)/2, (максимум+минимум+закрытие)/3, (открытие+максимум+минимум+закрытие)/4, % изменения или (открытие+закрытие)/2. Эти данные могут быть предварительно произвольно сглажены перед построением наиболее подходящей линии. Если сглаживание не желательно, то просто выбирается период сглаживания равный 1.

Вычисление   Для того, чтобы определить лучшую линию, соответствующую ряду ценовых точек, используется метод наименьшего квадрата.

Стандартное отклонение вычисляется следующим образом: - Суммируются квадраты разницы между ценой и линией Линейной регрессии. - Порлученная сумма делится на число баров в диапазоне регрессионного ряда данных. - Вычисляется квадратный корень от полученного результата, что дает стандартное отклонение.