
- •Предмет и система правовой статистики.
- •Особенности юридической статистики. Методологические особенности правовой статистики и ее связь с другими науками и учебными дисциплинами
- •Современная организация правовой статистики в Российской Федерации.
- •Научно-практическое значение материалов правовой статистики.
- •История уголовно-правовой статистики советского периода.
- •Понятие статистического наблюдения, этапы его проведения.
- •Организационные вопросы статистического наблюдения.
- •Ошибки регистрации и репрезентативности.
- •Единый учет преступлений и документы первичного учета в правоохранительных органах.
- •Выборочный метод. Генеральная и выборочная совокупность. Типы выборок.
- •Табличный и графический методы представления данных статистики.
- •Существуют правила построения таблиц:
- •Статистическое распределение выборки. Эмпирическая функция распределения. Свойства эмпирической функции распределения.
- •Определения
- •Свойства эмпирической функции распределения Эмпирическое распределение для фиксированного
- •Числовые характеристики статистического распределения (выборочные среднее, дисперсия, среднеквадратичное отклонение, мода, медиана, моменты, асимметрия и эксцесс, квантили).
- •Понятие дисперсии
- •Виды дисперсии
- •Правило сложения дисперсии в статистике
- •Свойства дисперсии
- •Основные сведения
- •[Править]Правило трёх сигм
- •[Править]Интерпретация величины среднеквадратического отклонения
- •[Править]Практическое применение
- •[Править]Климат
- •[Править]Спорт
- •[Править]Технический анализ
- •[Править]Пример использования
- •[Править]Определение
- •[Править]Замечания
- •[Править]Дециль
- •[Править]Перцентиль
- •[Править]Квантили стандартного нормального распределения
- •[Править]Определение
- •[Править]Замечания
- •[Править]Таблица квантилей
- •Оценка параметра и свойства оценок. Статистические оценки параметров распределения
- •Точечное оценивание параметров распределения.
- •Интервальное оценивание параметров распределения. Интервальное оценивание среднего квадратичного отклонения нормального распределения.
- •Статистическая гипотеза. Постановка задачи проверки статистических гипотез. Понятие статистической гипотезы
- •Ошибки первого и второго рода при проверке гипотез.
- •[Править]Определения
- •[Править]о смысле ошибок первого и второго рода
- •[Править]Вероятности ошибок (уровень значимости и мощность)
- •20. Проверка гипотез о законе распределения. Критерий согласия «Хи–квадрат» Пирсона
- •[Править]Статистика критерия
- •[Править]Правило критерия
- •Нормальный закон распределения и его основные характеристики.
- •[Править]Свойства
- •[Править]Моделирование нормальных случайных величин
- •[Править]Центральная предельная теорема
- •Статистические связи. Условное среднее. Причинная и функциональная связи. Статистическая связь
- •Парная корреляция. Уравнение регрессии. Линия регрессии.
- •[Править]Цели регрессионного анализа
- •[Править]Математическое определение регрессии
- •[Править]Метод наименьших квадратов (расчёт коэффициентов)
- •[Править]Интерпретация параметров регрессии
- •25. Корреляционный момент, коэффициент корреляции их свойства.
[Править]Дециль
Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля.
[Править]Перцентиль
![]() -ой перценти́лью называют
квантиль уровня
-ой перценти́лью называют
квантиль уровня ![]() .
При этом обычно рассматривают перцентили
для целых
,
хотя данное требование не обязательно.
Соответственно, медиана является 50-й
перцентилью, а первый и третий квартиль —
25-й и 75-й перцентилями.
.
При этом обычно рассматривают перцентили
для целых
,
хотя данное требование не обязательно.
Соответственно, медиана является 50-й
перцентилью, а первый и третий квартиль —
25-й и 75-й перцентилями.
В целом, понятия квантиль и перцентиль взаимозаменяемы, также, как и шкалы исчисления вероятностей — абсолютная и процентная.
Перцентили также называются процентилями или центилями.
[Править]Квантили стандартного нормального распределения
-
Уровень
0,9999
0,9990
0,9900
0,9772
0,9750
0,9500
0,9000
0,8413
0,5000
Квантиль
3,715
3,090
2,326
2,000
1,960
1,645
1,282
1,000
0,000
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
[Править]Определение
Пусть ![]() — функция
распределения Стьюдента
— функция
распределения Стьюдента ![]() с
степенями
свободы, и
с
степенями
свободы, и ![]() .
Тогда
-квантилью этого
распределения называется число
.
Тогда
-квантилью этого
распределения называется число ![]() такое,
что
такое,
что
![]() .
.
[Править]Замечания
Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с степенями свободы, не превышает значение с вероятностью и превышает его с вероятностью
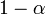 .
.Функция строго возрастает для любого
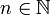 .
Следовательно, определена её обратная
функция
.
Следовательно, определена её обратная
функция 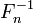 ,
и
,
и
![]() .
.
Функция не имеет простого представления. Однако, возможно вычислить её значения численно.
Распределение симметрично. Следовательно,
![]() .
.
[Править]Таблица квантилей
Нижеприведённая таблица
получена с помощью функции tinv пакета MATLAB.
Чтобы получить значение ![]() ,
необходимо найти строку, соответствующую
нужному
,
необходимо найти строку, соответствующую
нужному ![]() ,
числу степеней свободы, расчитываемому
по формуле
,
числу степеней свободы, расчитываемому
по формуле ![]() ,
и колонку, соответствующую нужному
.
Искомое число находится в таблице на
их пересечении. Если необходимо
использовать
,
не приведённое в таблице, то значения
можно получить в табличных редакторах
(в Excel функция СТЬЮДРАСПОБР; в O(L)office -
TINV). Кроме того, не следует путать
запись
и
,
и колонку, соответствующую нужному
.
Искомое число находится в таблице на
их пересечении. Если необходимо
использовать
,
не приведённое в таблице, то значения
можно получить в табличных редакторах
(в Excel функция СТЬЮДРАСПОБР; в O(L)office -
TINV). Кроме того, не следует путать
запись
и ![]() .
Во второй записи, которая очень часто
приводится в качестве ответа, речь идёт
о величине "p=1-
".
.
Во второй записи, которая очень часто
приводится в качестве ответа, речь идёт
о величине "p=1-
".
Оценка параметра и свойства оценок. Статистические оценки параметров распределения
Пусть x1,
x2,
…, xn –
выборка объема n из
генеральной совокупности с функцией
распределения F(x ).
Рассмотрим методы нахождения оценок
параметров этого распределения.
Рассмотрим для этого выборочное
распределение, т.е. распределение
дискретной случайной величины, принимающей
значения x1,
x2,
…, xn с
вероятностями, равными 1/n .
Числовые характеристики этого выборочного
распределения
называютсявыборочными (эмпирическими) числовыми
характеристиками. Следует
отметить, что выборочные числовые
характеристики являются характеристиками
данной выборки, но не являются
характеристиками распределения
генеральной совокупности. Однако эти
характеристики можно использовать для
оценок параметров генеральной
совокупности.
Точечной называют
статистическую оценку, которая
определяется одним числом.
Несмещенной называют
точечную оценку, математическое ожидание
которой равно оцениваемому параметру
при любом объеме выборки.
Точечная оценка называется состоятельной,
если при неограниченном увеличении
объема выборки (n =>
∞) она сходится по вероятности к истинному
значению параметра.
Эффективной называют
точечную оценку, которая (при заданном
объеме выборки n)
имеет наименьшую возможную дисперсию.
В математической статистике показывается,
что состоятельной, несмещенной оценкой
генерального среднего значения а
является выборочное среднее
арифметическое:
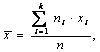 где хi –
варианта выборки, ni –
частота варианты хi,
–
где хi –
варианта выборки, ni –
частота варианты хi,
– ![]() объем
выборки.
Для упрощения
расчета целесообразно перейти к условным
вариантам
объем
выборки.
Для упрощения
расчета целесообразно перейти к условным
вариантам ![]() (в
качестве с выгодно
брать первоначальную варианту,
расположенную в середине вариационного
ряда). Тогда
(в
качестве с выгодно
брать первоначальную варианту,
расположенную в середине вариационного
ряда). Тогда
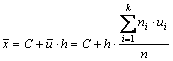 .
Эффективность или неэффективность
оценки зависит от вида закона распределения
случайной величины Х.
Если величина Х распределена
по нормальному закону, то оценка
.
Эффективность или неэффективность
оценки зависит от вида закона распределения
случайной величины Х.
Если величина Х распределена
по нормальному закону, то оценка ![]() является
эффективной. Для других законов
распределения это может быть и не
так.
Несмещенной
оценкой генеральной дисперсии служит
исправления выборочная дисперсия
является
эффективной. Для других законов
распределения это может быть и не
так.
Несмещенной
оценкой генеральной дисперсии служит
исправления выборочная дисперсия
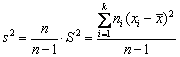 ,
так как
,
так как ![]() ,
где σ2 –
генеральная дисперсия. Более удобна
формула
,
где σ2 –
генеральная дисперсия. Более удобна
формула 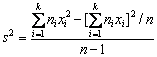 .
Если
.
Если ![]() .
Оценка s2 для
генеральной дисперсии является также
и состоятельной, но не является
эффективной. Однако в случае нормального
распределения она является «асимптотически
эффективной», то есть при увеличении n
отношение ее дисперсии к минимально
возможной неограниченно приближается
к единице.
Итак, если
дана выборка из распределения F(x)
случайной величины Х с
неизвестным математическим ожиданием а и
дисперсией σ2 ,
то для вычисления значений этих параметров
мы имеем право пользоваться следующими
приближенными формулами:
.
Оценка s2 для
генеральной дисперсии является также
и состоятельной, но не является
эффективной. Однако в случае нормального
распределения она является «асимптотически
эффективной», то есть при увеличении n
отношение ее дисперсии к минимально
возможной неограниченно приближается
к единице.
Итак, если
дана выборка из распределения F(x)
случайной величины Х с
неизвестным математическим ожиданием а и
дисперсией σ2 ,
то для вычисления значений этих параметров
мы имеем право пользоваться следующими
приближенными формулами:

