Понятие дисперсии

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

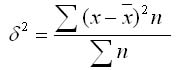
где n - частота (повторяемость фактора Х)

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

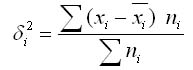
где хi — групповая средняя;  ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

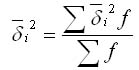
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

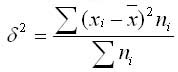
Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится. 2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.