29. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида

Рассмотрим след. Д. у.

Считается что f(x) – непрерывно на некотором промежутке

Как мы знаем общее решение имеет вид

Где y^*- частное решение неоднородного ур-я (1) а y₁,y₂…y_n- образуют фундамент. сист. решений однородного ур-я

Для нахождения общего решения исходного ур-я достаточно найти какое-либо его одно частное решение. Для специального вида правых частей f(x) ур-я (1) эта задача решается операцией дифференцирования и решением систем линейных алгебраических ур-й. Этот метод называется методом неопределённых коэф.

Правая часть для которой этот метод неприменим имеет вид :

(4)

Где P_m и Q_l – многочлены степеней m и l соотв.

Рассмотрим различные случаи правых частей ур-я (1):

Случай 1 :

Полагаем что A_m =/= 0 и λ=0 не является корнем хар-го ур-я (3), в этом случае y^* ищется в виде многочлена той-же степени

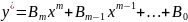(6)

Где B_m,…B₀- Коэф. Которые надо определить, чтобы их определить необходимо подставить ур-е (6) в ур-е (1) и сравнить коэф. При одинаковых степенях x правой и левой частях ур-я и получим систему линейных ур-й относительно B_k

В резонансном случае (λ =0) частное решение ищется в виде

(7)

Где x^k- резонансный множитель

Случай 2 : (9)

Если не корень хар-го ур-я L(λ)=0 то частное решение ур-я (1) ищется в виде

(10)

Где А_j – определяются методом неопр. коэф.

В резонансном случае ( - корень кратности к ур-я L(λ)=0) частное решение ищем в виде

(11)

Случай 3 : ( ) (12)

Если – не корень ур-я L(λ)=0 то частное решение ур-я (1) ищется в виде

( ) (13)

Где R_s и T_s – многочлены степени s причем s=max{m,l}

В случае когда - корень кратности к ур-я L(λ)=0 тогда решение ищется в виде

( ) (14)

Если же правая часть ур-я (1) имеет вид (4) то решение исходной системы находят с помощью принципа суперпозиции.

30.Линейные однородные системы дифф.Ур.

Линейной однородной системой наз. Нормальная линейная система д.у. вида =A(x)y (1), где А(х)-заданная непрерывная на [α;β] квадратная матрица порядка n,( а в некоторых случаях комплекснозначная).

Решениями данной системы будут некоторые вектор-функции с компонентами определёнными на [α;β]. Непосредственным образом проверяются следующие утверждение наз. принципом суперпозиции для системы (1).

Лемма 1: Если у1 и у2 есть решение системы (1), а С1 и С2-произвольные числа, то вектор функция у=С1у1+С2у2, также будет решением исходной системы (1).

Опр.1 :Вектор-функции у1,…,ук наз. линейно зависимыми на промежутке I, если найдутся такие числа С1,…,Ск одновременно не равные нулю, что имеет место тождество С1у1+…+Скук=0, в противном случае данные вектор-функции наз. линейно независимыми на промежутке I.

Лемма 2: Если вектор-функции j=1,..,k линейно зависимы на промежутке I, то при всех 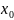ϵ I числовые векторы ( ) , j=1,..,k также линейно зависимы.

Обратное утверждение вообще говоря неверно.

Т.1: Пусть j=1,..,k есть решение системы (1) .Тогда данные решения j=1,..,k линейно независимы на [α;β] тогда и только тогда, когда для всякого ϵ [α;β] числовые векторы ( ) , j=1,..,k линейно независимы.

Следствие 1:Решения j=1,..,k системы (1.27) линейно зависимы на [α;β] тогда и только тогда, когда линейно зависимы числовые векторы ( ) , j=1,..,k.

Опр.2:Любая система n линейно независимых решений системы (1.27) на [α;β] назыв.фундаментальной системой решений(ФСР) этой системы.

Т. 2: Для системы (1) существует бесконечное множество ФСР.

Т.3: Если есть ФСР системы (1), то каждое решение y этой системы единственным образом представимо в виде , где -некоторые числа.

Рассмотрим начальные условия ϵ [α;β] (2).

Решение y каждой задачи Коши (1), (2) однозначно определяется с помощью вектор-функции (3), где -произвольные параметры.

(3)- общее решение системы (1).

Опр.3: Матрицу Ф(x) у которой столбцы образуют ФСР системы (1) будем назыв. фундаментальной матрицей этой системы.

Тогда общее решение (1) y(x)=Ф(x) C.

Рассмотрим на [α;β] матричные дифф.ур. (4) с неизвестной квадратной матрицей Y(x).

Пусть . Отсюда видно, что матрица тогда и только тогда будет решением ур. (4), когда её вектор-столбцы являются решениями системы (1). Значит фундаментальная матрица Ф(x) является решением уравнения (4). В силу не вырожденности фунд.матрицы получаем, что общее решение ФСР 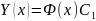, где С- произвольная квадратная матрица порядка n.

Имеем, что произвольная фунд.матрица системы (1) имеет представление .

Решение матричного дифф.ур.(4) с начальными условиями где I – единичная матрица назыв.матрицантом системы (4).

Матрица является матрицантом дифф.системы (1).

Опр.4: Определителем Вронского системы вектор-функций с n компонентами определёнными на [α;β] будем наз.следующий определитель

.

Т.4: Решение системы (1) линейно зависимы на [α;β] тогда и только тогда, когда на этом отрезке имеет место тождество

Т.5: Решение системы (1) линейно независимы на [α;β] тогда и только тогда, когда на этом отрезке Вронскиан W(x) не обращается в нуль.

Т.6: Пусть W(x) есть Вронскиан решений и точка ϵ [α;β]. Тогда имеет место формула Лиувиля-Остроградского

(5), где

- след матрицы A(x).