
- •Дать определение реальному объекту в расчетной системе.
- •В чем заключается метод сечений? с какой целью его используют?
- •Привести классификацию объектов по геометрической форме.
- •Записать основные гипотезы сопротивления материалов.
- •Дать понятие напряжения. Классификация напряжений.
- •Дать понятие деформации тела. Виды деформации.
- •Записать закон Гука при сдвиге. Пояснить входящие в формулу величины.
- •Что характеризует модуль упругости материала? в каких единицах он измеряется?
- •Пояснить продольную и поперечную деформации. Как они взаимосвязаны?
- •Дать определение коэфициенту Пуассона. Чему он численно равен?
- •Записать формулу для определения деформаций при растяжении и сжатии.
- •Привести диаграмму растяжений пластичного материала с указанием на ней всех характерных точек.
- •Привести диаграмму растяжений пластичного материала, охаректеризовать поведение материала в каждой зоне диаграммы.
- •Дать понятие, наклепу материалов, указав его вредное и полезное воздействие на примерах из практики.
- •Охарактеризовать чистый и поперечный изгиб. Привести примеры.
- •Записать формулу для определения нормальных напряжений при изгибе, привести их эпюру.
- •Записать условия прочности при изгибе.
- •Указать рациональную форму поперечного сечения балки при изгибе.
- •Показать, как строят эпюру касательных напряжений для двухтаврового поперечного сечения при изгибе.
- •Охарактеризовать напряженное состояние в точке тела.
Охарактеризовать чистый и поперечный изгиб. Привести примеры.
Изгиб – это такой вид нагружения, при котором в поперечных сечениях балки действуют два ВСФ,именно поперечная сила Q и изгибающий момент М.
Если в поперечном сечении дейст -вует только изгибающий момент, то такой изгиб называют чистым.
Все сечения при чистом изгибе находятся в равных условиях т.к. в них действует одинаковый по величине изгибающий момент. Точки лежащие в этих сечениях не имеют преимущественного смещения не влево не вправо.
Т.е при чистом изгибе справедливы гипотезы плоских сечений, следовательно, сам процесс чистого изгиба можно представить, как поворот на одинаковый угол каждого плоского сечения относительно общего центра, а лишь прогиба балки будет представлять собой дугу окружности. При изгибе одни волокна сжимаются, другие растягиваются, и существует слой волокн в котором деформация отсутствует – нейтральный.
Если поперечная сила и изгибающий момент – поперечным.
Изгибающий момент в каком - либо сечении балки численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от мысленно проведенного сечения относи –
ельно оси Х поперечного сечения балки.
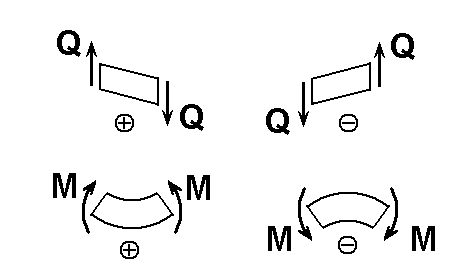
Он считается положительным, если растягивает нижние волокна балки и сжимает верхние.
Поперечная сила в каком - либо сечении балки численно равна алгебраической сумме всех внеш-них сил, действующих по одну сторону от мысленно проведен -ного сечения и спроецированных на ось У поперечного сечения балки.
Она считается положительной,
если стремится вращать ту часть балки равновесие которой
мы рассматриваем против часо -вой стрелки.
Записать формулу для определения нормальных напряжений при изгибе, привести их эпюру.
Напряжение - мера интенсивности распределения внутренних сил по сечению (сила, приходящаяся на единицу площади сечения)


Записать условия прочности при изгибе.

Указать рациональную форму поперечного сечения балки при изгибе.
Т.к. наибольшие напряжения возникают в наружных слоях сечения, а в центре равны 0, целесообразно убрать лишний метал из средних слоев. Так была получена следующие профили.
- двухтавр, швелер, коробчатые сечения.
Расмотрим двухтавр.
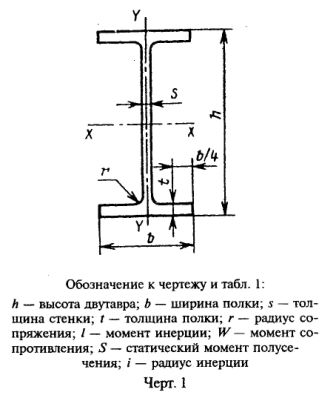
Построение эпюры выполняют по характерным точкам
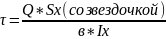
Q – поперечная сила, берется в сечении где момент достигает максимального значения, если Q=0 расчет выполняется для Qmax.
Sx(со звездочкой) – статический момент отсеченной части. Равен произведению площади отсеченой части на координату ее центра тяжести.
В- ширина отсеченой части.
Ix – осевой момент инерции (из табл.)
В галерее несколько фоток примера!!!!
Показать, как строят эпюру касательных напряжений для двухтаврового поперечного сечения при изгибе.
В галерее несколько фоток примера!!!!
Охарактеризовать напряженное состояние в точке тела.
