
- •Теоретические основы электротехники
- •Часть 2
- •Раздел 1
- •2Классический метод расчета переходных процессов
- •2.3Общие положения
- •2.4Задача и порядок расчета переходных процессов
- •2.6Включение конденсатора на постоянное напряжение
- •2.7Включение индуктивности на синусоидальное напряжение
- •2.8Включение цепи r, l, c на постоянное напряжение
- •2.9 Построение графиков зависимостей
- •2.10 Расчет переходных процессов в разветвленных цепях
- •3Операторный метод расчета переходных процессов
- •3.3Общие вопросы
- •3.4Переход от оригиналов к изображениям
- •3.5 Правила дифференцирования и интегрирования
- •3.6 Закон Ома в операторной форме
- •3.7 Второй закон Кирхгофа в операторной форме
- •3.8 Операторные схемы
- •3.9 Переход от изображений к оригиналам
- •3.10 Включение цепи r, l, c на постоянное напряжение
- •После преобразования получим
- •3.11 Передаточные функции
- •3.12Моделирование физических процессов с помощью электрических схем
3.4Переход от оригиналов к изображениям
Переход от одного вида в другой обозначается знаком соответствия:

![]() ,
(2.1)
,
(2.1)
и производится по прямому преобразованию Лапласа
![]() .
(2.2)
.
(2.2)
Пусть функцией является постоянная величина: f(t) = E . Используем преобразование Лапласа.
![]() ,
(2.3)
,
(2.3)
отсюда следует, что изображение постоянной функции равно постоянной, деленной на оператор р.
 .
.
 ;
(2.4)
;
(2.4)
![]() ,
,
![]() .
.
![]() ,
(2.5)
,
(2.5)
![]() .
(2.6)
.
(2.6)
![]() .
(2.7)
.
(2.7)
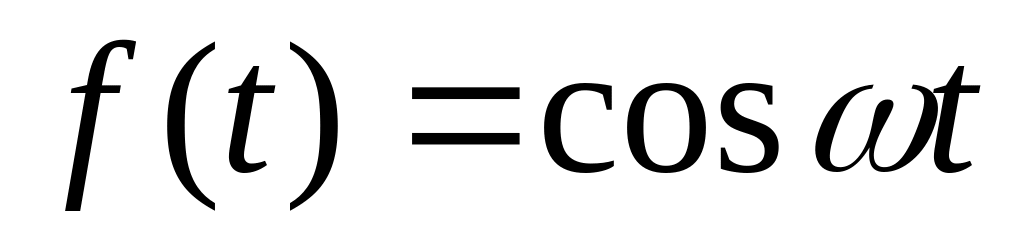 .
.
![]() (2.8)
(2.8)
3.5 Правила дифференцирования и интегрирования
П
усть
имеется функция и его изображение
![]() .
Возьмем производную от оригинала:
.
Возьмем производную от оригинала:
![]() . (2.9)
. (2.9)
Это новая функция времени. Определим ее изображение по преобразованию Лапласа.
![]() .
(2.10)
.
(2.10)
Воспользуемся методом интегрирования по частям:
![]() .
.
Введем обозначения
![]()
![]()
![]() .
(2.11)
.
(2.11)
Здесь второе слагаемое есть изображение оригинала, умноженное на оператор p, первое слагаемое раскрывается следующим образом. При подстановке верхнего предела первый сомножитель стремится к нулю. Второй сомножитель может стремиться к бесконечности. Однако все электротехнические функции стремятся к бесконечности медленнее, чем первый сомножитель к нулю. Поэтому произведение равно нулю.
Подстановка нижнего предела дает начальное условие. Таким образом
![]()
![]() .
(2.12)
.
(2.12)
Окончательно:
![]() .
.
Если начальные условия нулевые, т.е. – f(0) = 0, то
![]() .
.
О тсюда следует, что дифференцированию оригинала соответствует умножению изображения на оператор р.
2. Пусть функция имеет изображение: f(t) == F(p). Возьмем интеграл от оригинала
 .
(2.13)
.
(2.13)
Применим преобразование Лапласа к данной функции
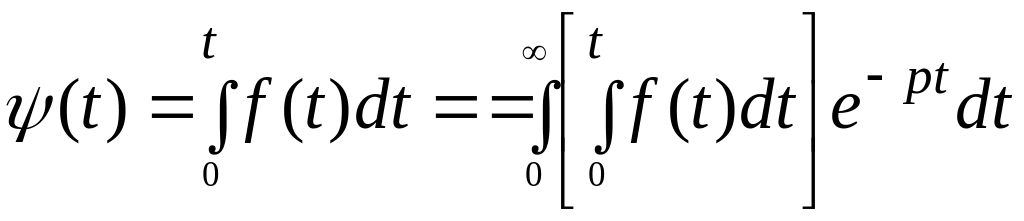 .
(2.14)
.
(2.14)
Этот интеграл можно взять так же по частям. Но если t=0 , то ψ (0 ) = 0. Тогда
![]() ,
(2.15)
,
(2.15)
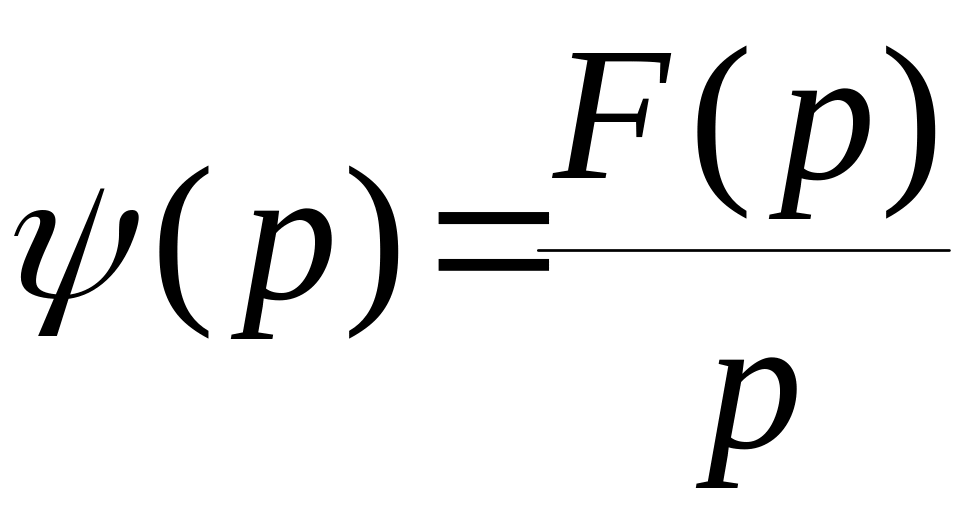 .
(2.16)
.
(2.16)
Интегрированию оригинала соответствует делению изображения функции на оператор р .
