А кадемия управления при Президенте Республики Беларусь

Задания и упражнения для практических занятий

(для специальностей

«Государственное управление и экономика» и «Управление информационными ресурсами»)

Минск 2004

1 Теория пределов 3

Элементы дифференциального исчисления 9

2 Дифференциальное исчисление функций нескольких переменных. 16

3 Экстремумы функций нескольких переменных. 20

4 Элементы интегрального исчисления (неопределенные интегралы) 21

5 Определенные и кратные интегралы 25

6 Ряды 31

7 Знакомство с обыкновенными дифференциальными уравнениями (ОДУ). 37

1Теория пределов

Практическое занятие 1. Вычисление пределов последовательностей. Понятие функции.

Вопросы для повторения

1. Определение предела последовательности.

2. Первый и второй замечательные пределы.

3. Понятие функции, области определения и множества значений функции.

4. Понятие четности, нечетности и периодичности функции.

Предел последовательности.

Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: .

Число называют пределом последовательности . При этом записывают или .

Найти первые четыре члена последовательности (a_n), если

Ответы:

Найти общий член последовательности

Ответы:

Пример. Пользуясь определением предела числовой последовательности, доказать, что последовательность имеет предел .

Решение. Нам надо доказать, что, какое бы мы ни взяли, для него найдется число , такое, что для всех имеет место неравенство.

Возьмем любое . Так как , то для отыскания достаточно решить неравенство . Отсюда и, следовательно, за можно принять . Мы тем самым доказали, что .

Пользуясь определением предела числовой последовательности, доказать, что последовательность имеет предел .

1. ; .

2. ;

3. ;

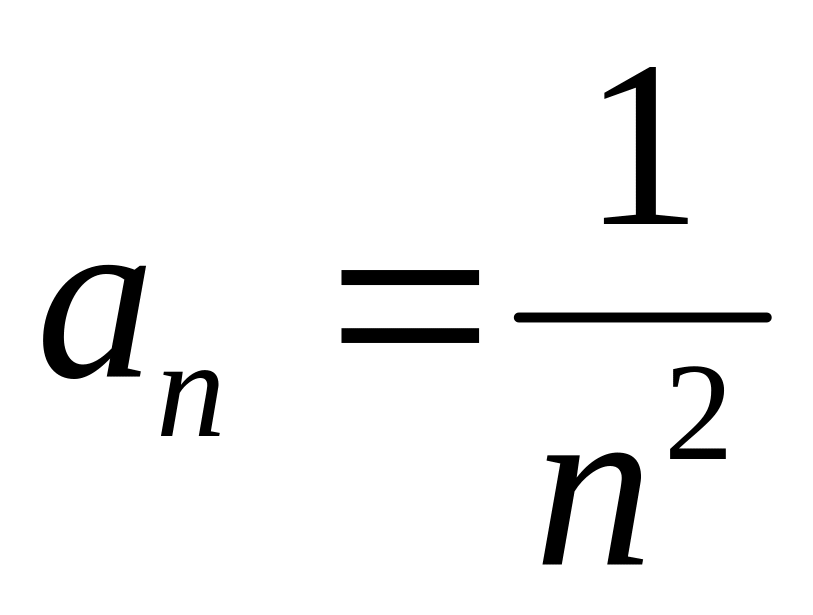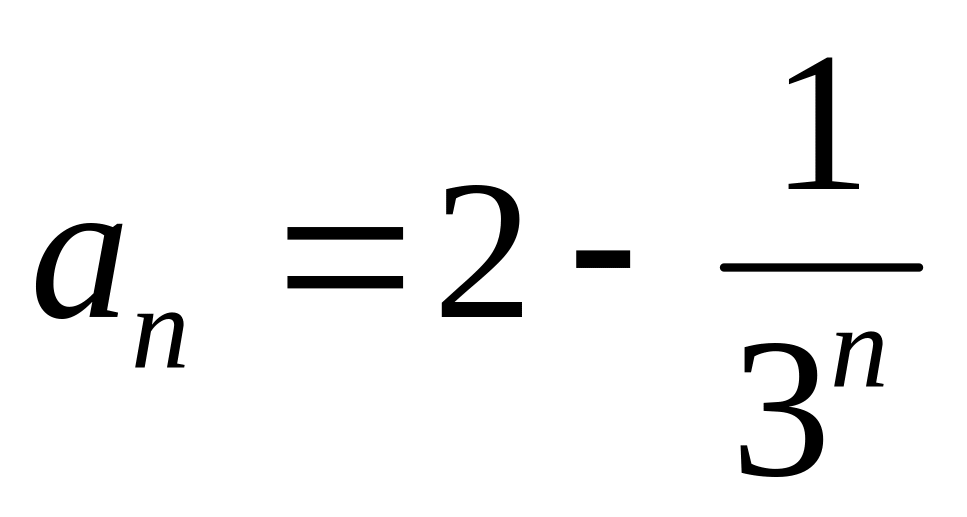Пример. Найти .

Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида  - . Преобразуем формулу общего члена:

.

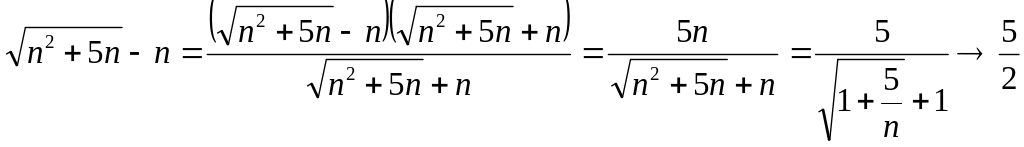Найти пределы последовательности при

Ответы:

0

0

Первый и второй замечательные пределы.

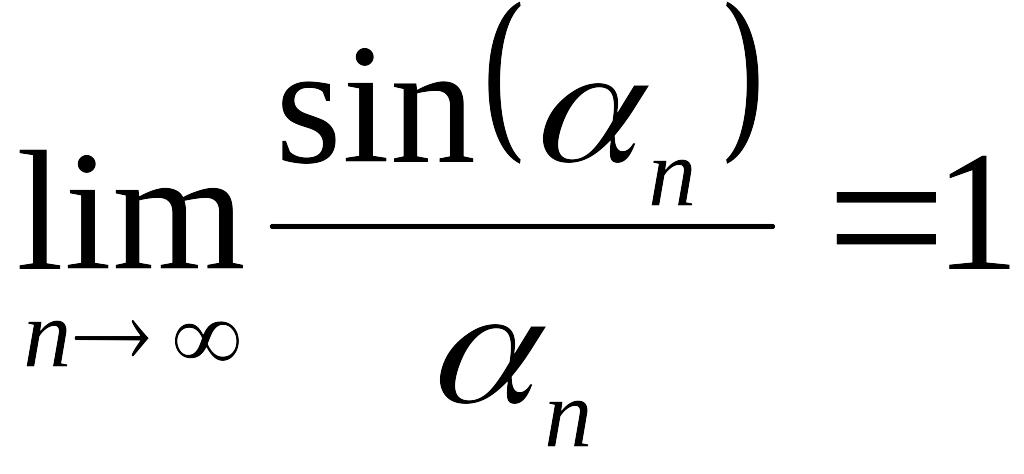1. , где

2. 

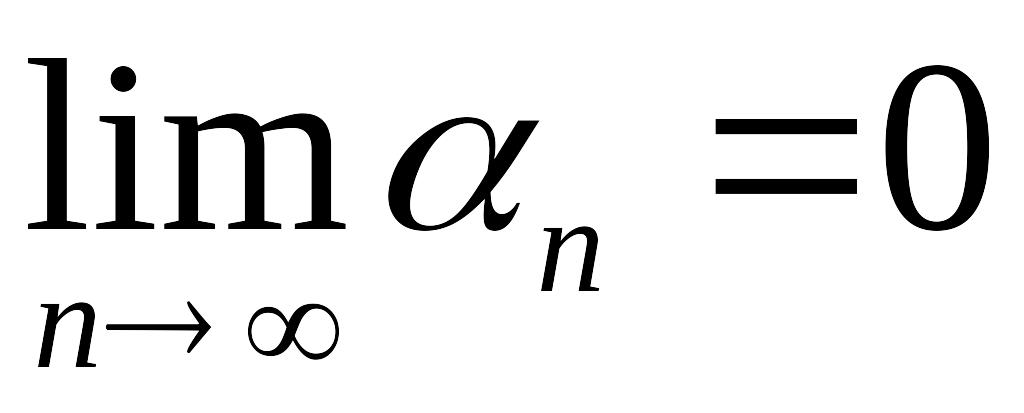
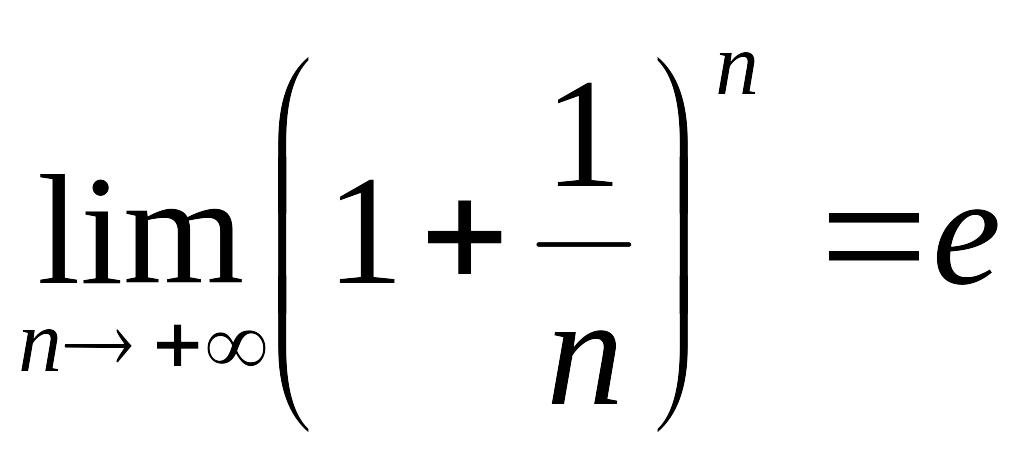
Найти пределы последовательности при используя замечательные пределы

Ответы:

1

Понятие функции, области определения и множества значений функции.

Пусть ‑ некоторое числовое множество и пусть задан закон (правило) , по которому каждому числу ставится в соответствие единственное число обозначаемое . Тогда говорят, что на множестве задана функция и записывают: или

Чаще записывают и говорят проще: задана функция ,

Множество называют областью определения функции . Множество называют множеством значений функции . При этом называют независимой переменной или аргументом функции, – зависимой переменной или значением функции, а – характеристикой функции.