23. Дерево. Назначение, варианты реализации и примеры применения.

 

Деревья вокруг нас

Дерево это иерархическая структура, состоящая из узлов и соединяющих их дуг. В каждый узел, кроме одного, ведет ровно одна дуга. Этот единственный узел называется корнем дерева.

Многие отношения, которые встречаются в жизни и в программировании, можно изобразить в виде деревьев.

Обратите внимание на компьютерную программу. Ее блоки составляют дерево, дуги которого означают вложенность. Взаимная вложенность операторов цикла, условных операторов, составных, — все это деревья. Даже арифметические выражения представляют собой деревья, в узлах которых операции

Рекурсивное определение дерева

Дуги ведут к узлам дерева. Иная точка зрения состоит в том, что дуги ведут к частям дерева, которые сами являются деревьями. Она приводит к рекурсивному определению дерева: «Дерево — это пустая структура или узел, связанный дугами с конечным числом деревьев».

Пустое дерево — то же, что пустой список. Вообще, есть близкое родство между деревом и списком.

Рекурсивное и нерекурсивное определения дерева равносильны, но из второго можно извлечь много полезных алгоритмов.

Двоичные упорядоченные деревья

В упорядоченных массивах можно быстро найти нужную информацию. Динамические списки можно быстро пополнить новыми элементами. Двоичные упорядоченные деревья соединяют в себе оба этих качества.

Двоичное дерево упорядочено, если все ключи левого поддерева каждого узла меньше, чем ключ узла, а ключи правого поддерева — больше (ключом называется признак, по которому ведется поиск).

Поиск в упорядоченном дереве выполняют рекурсивным алгоритмом очень похожим на алгоритм двоичного поиска.

1. Если дерево не пусто, то нужно сравнить искомый ключ с тем, что в корне дерева:

— если ключи совпадают, поиск завершен;

— если ключ в корне больше искомого, выполнить поиск в левом поддереве;

— если ключ в корне меньше искомого, выполнить поиск в правом поддереве.

2. Если дерево пусто, поиск неудачен. Продолжительность поиска определяется длиной одной ветви дерева. Если ветви примерно одинаковы {дерево сбалансировано), то время поиска в дереве с N узлами такое же, как время двоичного поиска в упорядоченном массиве из N элементов N—1

Алгоритм поиска легко переделать в алгоритм включения нового узла в упорядоченное дерево. Для этого достаточно слова «поиск неудачен» заменить словами «включаем новый узел в качестве правого (левого) поддерева».

При удалении узла из дерева возможны следующие случаи:

1) удаляемый узел не имеет поддеревьев;

2) удаляемый узел имеет лишь одно поддерево;

3) удаляемый узел имеет оба поддерева.

В первом случае достаточно убрать ссылку на удаляемый узел в родительском узле. Во втором случае следует заменить в родительском узле ссылку на удаляемый узел ссылкой на его поддерево. В третьем случае надо заменить удаляемый узел самым левым узлом его правого поддерева или самым правым узлом его левого поддерева.

Деревья относятся к разряду структур, которые удобно строить в динамической памяти с использованием указателей. Наиболее важный тип деревьев – двоичные (бинарные) деревья, в которых каждый узел имеет самое большее два поддерева: левое и правое. Подробнее, если имеем дерево вида (рис. 1a), то ему может соответствовать в динамической памяти структура (рис. 1б).

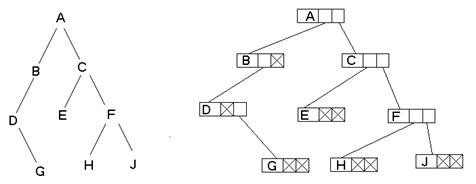а                                                   б Рис.1. Двоичное дерево и его представление с помощью списочных структур памяти а – двоичное дерево; б – представление дерева с помощью списков с использованием звеньев одинакового размера

Для построения такого бинарного дерева используется следующий ссылочный тип:

Type Ptr=^Node;  Node=record    Info=Char;    Llink,Rlink=Ptr;  End;

Для работы с деревьями имеется множество алгоритмов. К наиболее важным относятся задачи построения и обхода деревьев. Пусть в программе дано описание переменных:

var t:ptr;s:integer; c:char;b:boolean;

Тогда двоичное дерево можно построить с помощью следующей рекурсивной процедуры:

procedure V(var t:ptr);  var st:string; begin    readln(st);   if st<>'.'then       begin         new(t);         t^.info:=st;         V(t^.Llink);         V(t^.Rlink);       end      else t:=nil end;

Структура дерева отражается во входном потоке данных: каждой вводимой пустой связи соответствует условный символ (в данном случае точка). Для примера на рис. 1 входной поток имеет вид:

A B D . G . . C E . . F H . . J . . .

Существует три основных способа обхода деревьев [1]: в прямом порядке, обратном и концевом. Обход дерева может быть выполнен рекурсивной процедурой и процедурой без рекурсии (стековый обход). В приведенной ниже рекурсивной процедуре выполняется обход дерева в обратном порядке.

procedure PR(t:ptr); {рекурсивный обход дерева}  begin if t<>nil then   begin   PR(t^.Llink); {обойти левое поддерево}  writeln(t^.info); {попасть в корень}   PR(t^.Rlink); {обойти правое поддерево} end;end;

Нерекурсивный алгоритм обхода дерева в прямом порядке:

Пусть T – указатель на бинарное дерево; А – стек, в который заносятся адреса еще не пройденных вершин; TOP – вершина стека; P – рабочая переменная.

1.         Начальная установка: TOP:=0; P:=T.

2.         Если P=nil, то перейти на 4. {конец ветви}

3.         Вывести P^.info. Вершину заносим в стек: TOP:=TOP+1; A[TOP]:=P; шаг по левой ветви: P:=P^.llink; перейти на 2.

4.         Если TOP=0, то КОНЕЦ.

5.         Достаем вершину из стека: P:=A[TOP]; TOP:=TOP-1;  Шаг по правой связи: P:=P^.rlink; перейти на 2.