1. Определители

Определитель квадратной матрицы A есть ее числовая характеристика, обозначаемая 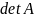или 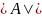. Начнем с определителей матриц малых размерностей 1,2,3:

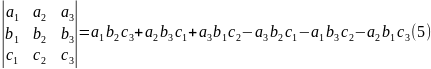
ОПРЕДЕЛЕНИЕ. Пусть -- n×n-матрица (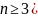 . Определителем матрицы A называется число, которое вычисляется по следующему правилу

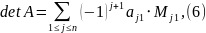
где 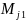-- определитель матицы, полученной из 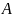вычеркиванием первого столбца и j-ой строки.

ТЕОРЕМА 1. Определитель треугольной матрицы равен произведению элементов на главной диагонали. В частности, .

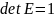Доказательство – индукция по 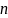с разложением по первому столбцу.□

Перечислим свойства определителей ( все они проверяются непосредственно для 2х2 и 3х3-матриц).

Свойство 1. Определитель матрицы равен определителю транспонированной матрицы.

Функция переменных вида 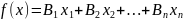называется линейной. Она обладает свойством

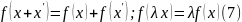
Наоборот, любая функция n переменных, обладающая свойством (7) линейна.

Свойство 2 (полилинейность). Определитель -- линейная функция от каждой строки (каждого столбца) матрицы.

Свойство 3 (кососимметричность). Определитель меняет знак при перемене местами двух строк (двух столбцов).

Свойство 4. Определитель равен нулю, если какие-либо две строки (два столбца) совпадают.

Свойство 5. Определитель с нулевой строкой (столбцом) равен нулю.

Свойство 6. Определитель не изменится, если над строками совершить элементарное преобразование первого типа, т.е. к одной строке прибавить другую, умноженную на какое-либо число. То же верно и для столбцов.

ОПРЕДЕЛЕНИЕ. -ым минором матрицы A называется определитель матрицы, получающейся из A вычеркиванием i -ой строки и j -го столбца. Обозначаем этот минор -- 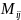. Алгебраическим дополнением –го элемента матрицы A называется величина .

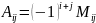Свойство 7. Разложение определителя по j -му столбцу и i -ой строке:

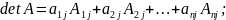
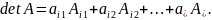
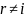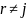Имеют место также ложные разложения по r -ой строке и r -ому столбцу; если и , то

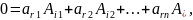
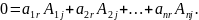
ТЕОРЕМА. Определитель произведения матриц равен произведению определителей: 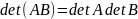(для любых 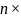-матриц и ).

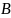2. Обратная матрица

ОПРЕДЕЛЕНИЕ. n×n -матрица D называется обратной к n×n-матрице A , если AD=DA=E . Обратная матрица единственна и обозначается как .

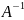ТЕОРЕМА. Обратная матрица к n×n -матрице A существует тогда и только тогда, когда матрица A невырождена (т.е. det A≠ 0). В этом случае

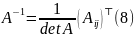
где 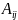-- алгебраическое дополнение к (i,j) -тому элементу матрицы. A . В частности, для 2× 2-матрицы

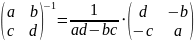
3. Компьютерная реализация матричной алгебры

Как отмечено выше, сами матрицы реализуются как двумерные массивы. Операции над матрицами в VBA реализуются так (см. файл Матричная алгебра.xlsm)

Sub primer1()' Умножение и обращение матриц Const n = 4 'размер матриц Dim MatA(1 To n, 1 To n) As Single ‘Тип вещественного числа Dim MatB(1 To n, 1 To n) As Single Dim MatC(1 To n, 1 To n) As Single

For i = 1 To n For j = 1 To n MatA(i, j) = Cells(i, j + 1): MatB(i, j) = Cells(i + 9, j + 1) Next j Next i

For i = 1 To n For j = 1 To n MatC(i, j) = Application.MMult(MatA, MatB)(i, j) ’Функция MMult встроена именно в Excel, но не в VBA. ‘ Индексация у рез-та этой функции начинается с 1 Next Next

'Распечатка For i = 1 To n For j = 1 To n Cells(i + 9, j + 10) = Application.MInverse(MatB)(i, j) Next j Next i For i = 1 To n For j = 1 To n Cells(i, j + 10) = MatC(i, j) Next j Next i Cells(19, 11) = Application.MDeterm(MatB)

End Sub