- •Спасское Городище 2012
- •Введение
- •Список обозначений и терминов
- •Немного о бейсиКе
- •Делимость целых чисел
- •Алгоритм Евклида
- •Матричная алгебра
- •Определители
- •Обратная матрица
- •Компьютерная реализация матричной алгебры
- •Линейные преобразования плоскости
- •Комплексные числа
- •Конструкция поля комплексных чисел.
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Решение квадратных уравнений.
- •Основная теорема алгебры комплексных чисел
- •Алгебраические системы
- •Операции и отношения на множестве
- •Моноиды
- •Поля и тела
- •Подсистемы алгебраических систем
- •Декартово произведение алгебраических систем
- •Фактор системы
- •Изоморфизм алгебраических систем
- •Абелевы группы
- •Группа подстановок
- •Алгебра многочленов
- •Немного комбинаторики
- •Биномиальные коэффициенты
- •Числа Фибоначчи
- •Рациональные числа
- •Дерево Штерна-Брокко
- •Алгебра высказываний
- •Дизъюнктивная совершенная нормальная форма.
- •Конъюнктивная нормальная совершенная форма
- •Многочлены Жегалкина
- •Алгебра кватернионов.
- •Литература
Дизъюнктивная совершенная нормальная форма.
Булевы
переменные будем обозначать
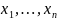 .
Строку булевых переменных обозначаем
.
Строку булевых переменных обозначаем
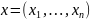 .
Для
.
Для
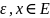 обозначим
обозначим
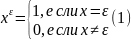
Мы видим,
что это просто другое обозначение
операции эквивалентности. Если
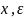 -- булевы строки длины n как и выше, то
обозначим
-- булевы строки длины n как и выше, то
обозначим
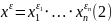
Для подмножества
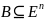 обозначим через
обозначим через
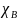 ее характеристическую функцию
,
принимающую значение 1 на строках из B
и принимающую значение 0 на строках из
дополнения
ее характеристическую функцию
,
принимающую значение 1 на строках из B
и принимающую значение 0 на строках из
дополнения
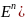 .
.
ЛЕММА.
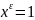 тогда и только тогда, когда
тогда и только тогда, когда
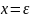 .
.
ТЕОРЕМА 2.
Имеет место равенство
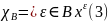
Для любой булевой функции
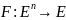 обозначим через
обозначим через
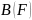 множество
множество
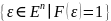 .
Тогда
.
Тогда
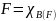 и представление функции F
в виде (3) называется дизъюнктивной
нормальной совершенной формой функции
.
и представление функции F
в виде (3) называется дизъюнктивной
нормальной совершенной формой функции
.
Заметим, что ДСНФ не всегда экономна. Например, обозначая операцию отрицания штрихом, будем иметь:
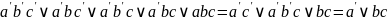
Первое
равенство объясняется так
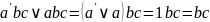 .
Второе можно проверить непосредственно,
подставляя
.
Второе можно проверить непосредственно,
подставляя
Конъюнктивная нормальная совершенная форма
Для булевой
функции
обозначим
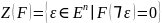 .
.
ТЕОРЕМА 3.
Имеет место равенство
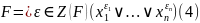
Две различные формы вида (4) задают различные булевы функции
Доказательство.
А. Проверим, что F равна 0 тогда и только
тогда, когда правая часть в (4) равна 0.
Пусть
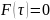 и тем самым
и тем самым
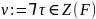 .
Тогда для
.
Тогда для
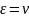 выполняется равенство
выполняется равенство
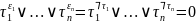 ,
ибо каждая компонента равна 0. Следовательно,
значение конъюнкции в (4) равно 0.
,
ибо каждая компонента равна 0. Следовательно,
значение конъюнкции в (4) равно 0.
Наоборот,
пусть значение правой части в (4) при
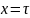 равно 0. Это значит, что для некоторого
равно 0. Это значит, что для некоторого
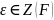 сомножитель
сомножитель
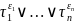 равен
0. Это может быть только если
равен
0. Это может быть только если
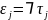 для любого j. Тогда
для любого j. Тогда
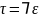 и
и
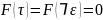 по определению множества
по определению множества
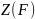 .
.
В. Пусть две
формы
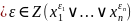 и
и
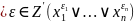 задают одинаковую булеву функцию. Первая
форма принимает значение 0 только для
строк
таких, что
задают одинаковую булеву функцию. Первая
форма принимает значение 0 только для
строк
таких, что
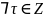 ,
а вторая для тех
,
что
,
а вторая для тех
,
что
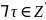 .
Отсюда
.
Отсюда
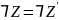 .
Так как отображение
.
Так как отображение
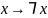 – биекция на множестве строк, то
– биекция на множестве строк, то
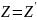 .
.
По другому
можно рассуждать так: форм вида (4) столько
же сколько подмножеств в
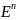 ,
т.е.
.
Это число совпадает с множество различных
булевых функций с n
переменными. В силу утверждения А, если
две формы вида (4) дают одинаковые функции,
то получается, что число разных булевых
функций будет строго меньше
.
Это противоречит теореме 1 □
,
т.е.
.
Это число совпадает с множество различных
булевых функций с n
переменными. В силу утверждения А, если
две формы вида (4) дают одинаковые функции,
то получается, что число разных булевых
функций будет строго меньше
.
Это противоречит теореме 1 □
Разложение (4) называют конъюктивной нормальной совершенной формой.
Многочлены Жегалкина
ПРЕДЛОЖЕНИЕ.
Эквивалентность
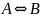 равна булевой функции
равна булевой функции
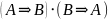 .
.
Импликация
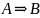 эквивалентна
эквивалентна
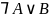 .
.
Дизъюнкция
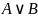 есть то же самое, что и
есть то же самое, что и
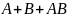
Отрицание
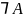 по другому выражается как
по другому выражается как
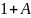 .
.
Доказательство вытекает из таблиц истинности этих функций.
ТЕОРЕМА 4.
Любая булева функция переменных может быть записана в виде
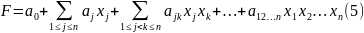
где
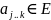
Количество слагаемых в суммах (5) есть
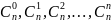 (включая первое и последнее слагаемые)
(включая первое и последнее слагаемые)
Набор коэффициентов
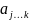 (их
(их
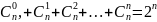 штук) однозначно определяется функцией
F
штук) однозначно определяется функцией
F
Доказательство.
Учитываем, что
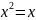 для булевой переменной
для булевой переменной
Алгебра кватернионов.
Кватернионы были изобретены немецким математиком Гамильтоном в 1843 году. Это был первый пример конечномерной некоммутативной алгебры над полем действительных чисел, в которой каждый ненулевой элемент обратим (т. е. алгебры с делением или тела). Как потом оказалось, это был и последний пример такой алгебры, ибо конечномерная алгебра с делением над ℝ есть либо само поле ℝ, либо поле комплексных чисел ℂ, либо тело кватернионов ℍ согласно теореме Фробениуса (см.[В], глава 11, §6, теорема 4). Произвольный элемент q∈ ℍ однозначно записывается в виде
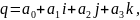
где
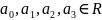 .
Если
.
Если
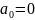 , то такой кватернион называется чистым.
Во-первых, превратим ℍ
в четырехмерное линейное пространство
на полем ℝ,
складывая кватернионы и умножая их на
числа покомпонентно. Таблица умножения
базисных элементов такова
, то такой кватернион называется чистым.
Во-первых, превратим ℍ
в четырехмерное линейное пространство
на полем ℝ,
складывая кватернионы и умножая их на
числа покомпонентно. Таблица умножения
базисных элементов такова
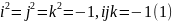
Из этих равенств получаем следствия:
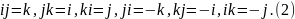
Так как умножение базисных элементов ассоциативно, то и ℍ -- ассоциативная алгебра.
Чистые
кватернионы образуют подпространство
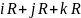 ,
которое будем отождествлять с трехмерным
линейным евклидовым пространством со
стандартным базисом i,j,k.
Для вычисления результата умножения
двух кватернионов используем скалярное
и векторное произведения. Операцию
скалярного произведения между векторами
a,b придется обозначать,
например, как a*b, оставив a⋅
b для обозначения произведения
кватернионов. Итак, если даны два
кватерниона q=a+a и t=b+b , где
a,b -- чистые кватернионы, а
a,b -- числа, то можно убедиться, что
,
которое будем отождествлять с трехмерным
линейным евклидовым пространством со
стандартным базисом i,j,k.
Для вычисления результата умножения
двух кватернионов используем скалярное
и векторное произведения. Операцию
скалярного произведения между векторами
a,b придется обозначать,
например, как a*b, оставив a⋅
b для обозначения произведения
кватернионов. Итак, если даны два
кватерниона q=a+a и t=b+b , где
a,b -- чистые кватернионы, а
a,b -- числа, то можно убедиться, что
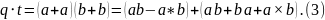
Записывая q и t более подробно и вспоминая записи скалярного и векторного произведений через координаты, получим:
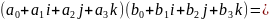
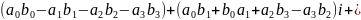
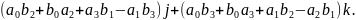
Кватернион
a-a назовем сопряженным к кватерниону
q=a+a и будем его обозначать
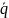 . Нетрудно проверить, что
. Нетрудно проверить, что
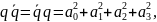
и поэтому
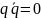 тогда и только тогда, когда q=0 . Величина
тогда и только тогда, когда q=0 . Величина
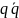 называется нормой кватерниона q и
обозначается
называется нормой кватерниона q и
обозначается
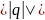 ,
а арифметический корень из нормы
называется модулем кватерниона q и
обозначается
,
а арифметический корень из нормы
называется модулем кватерниона q и
обозначается
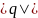 . Имеет место следующее утверждение:
. Имеет место следующее утверждение:
ТЕОРЕМА.
Множество кватернионов относительно
определенных выше операций сложения и
умножения образует алгебру с делением
над полем действительных чисел. Каждый
ненулевой кватернион q имеет обратный
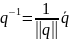 .
.
Уже отмечалось,
что алгебра кватернионов ассоциативна.
Она не коммутативна, так как, например,
ij≠ ji
. Проверим теперь, что кватернион
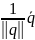 обратен к ненулевому кватерниону q.
обратен к ненулевому кватерниону q.
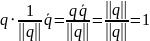
Отображение
ℂ →
ℍ (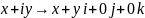 )
будет вложением поля комплексных чисел
в алгебру кватернионов. С таким же
успехом подходят для вложения отображения
)
будет вложением поля комплексных чисел
в алгебру кватернионов. С таким же
успехом подходят для вложения отображения
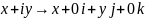 и
и
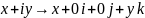 .
Однако ℍ не
является алгеброй над полем комплексных
чисел, ибо "мнимые единицы" i,j,k
не лежат в центре ℍ.
.
Однако ℍ не
является алгеброй над полем комплексных
чисел, ибо "мнимые единицы" i,j,k
не лежат в центре ℍ.
Пусть
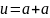 -- ненулевой кватернион. Отображение
сопряжения
-- ненулевой кватернион. Отображение
сопряжения
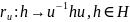
есть автоморфизм
алгебры кватернионов. Это означает, что
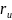 -- биекция (у него есть обратное отображение
-- биекция (у него есть обратное отображение
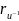 )
и
)
и
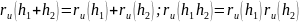 для любых кватернионов
для любых кватернионов
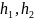 .
Проверим, что
.
Проверим, что
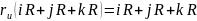
Достаточно
установить, что
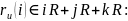
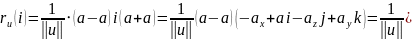
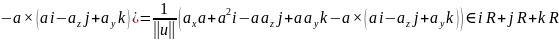
Далее,
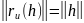 ,
следовательно, это (очевидно линейное)
преобразование пространства
ортогонально. Так как
,
следовательно, это (очевидно линейное)
преобразование пространства
ортогонально. Так как
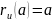 ,
то преобразование сопряжения
есть поворот на угол
,
то преобразование сопряжения
есть поворот на угол
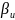 относительно вектора
.
Как найти угол
.
Пусть
-- перпендикулярен вектору
.
Тогда
относительно вектора
.
Как найти угол
.
Пусть
-- перпендикулярен вектору
.
Тогда
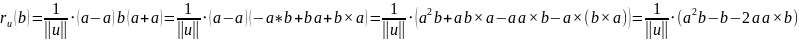
Пусть
– вектора единичной длины. Тогда на
плоскости
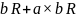 в базисе
в базисе
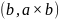 поворот, индуцированный сопряжением,
задается матрицей
поворот, индуцированный сопряжением,
задается матрицей
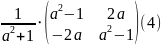
Отсюда следует, что
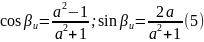
ПРИМЕР.1)
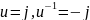 и
и
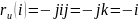 -- поворот на
-- поворот на
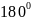 .
Это же следует из (5) в котором полагаем
.
Это же следует из (5) в котором полагаем
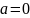 .
.
2)
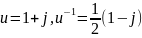 и
и
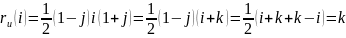
-- поворот на
угол
.
Это следует так же из (5), в котором
полагаем