5. Поля и тела

Ненулевое кольцо, в котором каждый ненулевой элемент обратим, называется телом. Коммутативное тело называется полем. Более точно: алгебраическая система 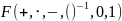, где “+,⋅ “ -- бинарные операции, -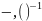 -- унарные операции, причем вторая из них частичная, 0 и 1 – 0-арные операции называется полем, если выполнены следующие аксиомы

П1. (ассоциативность) ;

П2. (коммутативность) ;

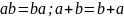П3. (дистрибутивность) ;

П4. ;

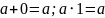П5. 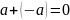; если , то ;

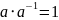П6. 0≠ 1

Известны «классические» поля рациональных и действительных чисел. Другие примеры полей, также как и пример тела, появятся позже.

6. Подсистемы алгебраических систем

Непустое подмножество 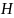алгебраической системы G называется подсистемой, если оно замкнуто относительно всех операций, входящих в сигнатуру системы. Тем самым H можно рассматривать как алгебраическую систему с той же самой сигнатурой.

Если алгебраическая система имеет специальное название (моноид, группа, кольцо, поле), то название подсистемы получается прибавлением приставки «под» к этому названию (подмоноид, подгруппа, подкольцо, подполе).

Например, ℚ есть подполе поля ℝ. В этом случае говорят, что большее поле есть расширение меньшего. Верхнетругольные (нижнетреугольные) матрицы n×n составляют подкольцо в кольце Mat(n×n;R). Вообще в алгебре матриц очень много подколец. Пусть 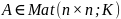(K – поле). Обозначим

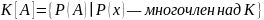
-- алгебру, порожденную над К матрицей A. Свойства этой алгебры отражают свойства матрицы А. В частности, унитарный многочлен наименьшей степени 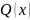с коэффициентами из поля К такой, что 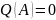называется минимальным многочленом матрицы А, и его степень совпадает с размерностью K[A] как линейного пространства над K.

В группе обратимых n×n-матриц над полем (или кольцом) К (обозначается GL(n,K) и называется общей линейной группой) также много подгрупп:

SL(n,K) – группа n×n-матриц с единичным определителем, называемая специальной линейной группой.

UT(n,K) – группа верхнетреугольных матриц с единицами на главной диагонали

Diag(n,K) – группа обратимых диагональных матриц

SL(2,ℤ ;p) -- группа унитарных целочисленных матриц, у которых на побочной диагонали стоят элементы кратные p. Это, так называемая конгруэнц-подгруппа.

7. Декартово произведение алгебраических систем

Пусть 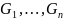-- алгебраические системы с одной и той же сигнатурой. Определим на декартовом произведении 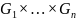операции из этой сигнатуры покомпонентно:

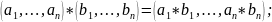
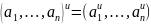
Получаем алгебраическую систему того же класса.

Часто употребляют эту конструкцию, когда все 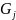-- одна и та же алгебраическая система . Тогда обозначают и называют декартовой степенью.

8. Фактор системы

Пусть ~ -- отношение эквивалентности на алгебраической системе . Скажем, что оно согласовано с операциями этой системы, если

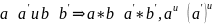
Аналогично определяется согласованность отношения ~ с любой n-арной операцией. Обозначим через 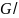множество классов эквивалентности. Определим на этом множестве те же самые операции:

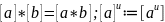
Эти определения корректны, т.е. результат в правой части не зависит от представителей классов эквивалентности в левой части.

Полученная таким образом алгебраическая система называется фактор системой.

Если алгебраическая система имеет специальное название (моноид, группа, кольцо), то название фактор системы получается прибавлением слова «фактор» к этому названию (фактор моноид, фактор группа, фактор кольцо).

Мы уже отмечали одну фактор систему, точнее фактор кольцо кольца целых чисел (пример «к» в начале этого параграфа). Отношение эквивалентности в этом случае задается так: 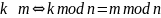. Из свойств делимости вытекает его согласованность с операциями сложения и умножения.