Гл. 6. Матрицы и определители.

§1 Понятие матрицы. Операции над матрицами.

1. Определения.

Определение: Матрицей размерности называется прямоугольная таблица содержащая - строк и - столбцов:

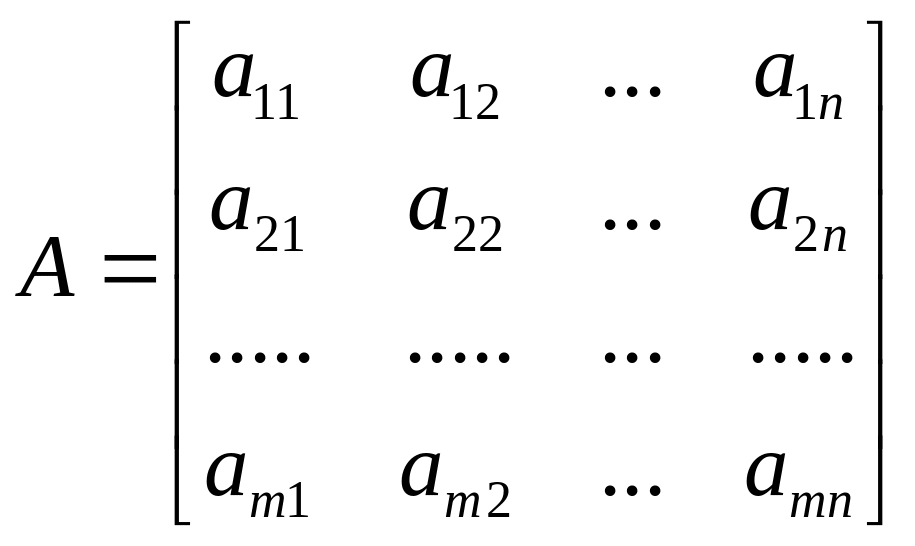
- элемент матрицы , - номер строки, - номер столбца.

Элементами матрицы могут быть действительные комплексные числа, переменные, а так же сами матрицы.

Матрица состоящая из одной строки, называется матрица – строка, матрица состоящая из одного столбца – матрица столбец:

, .

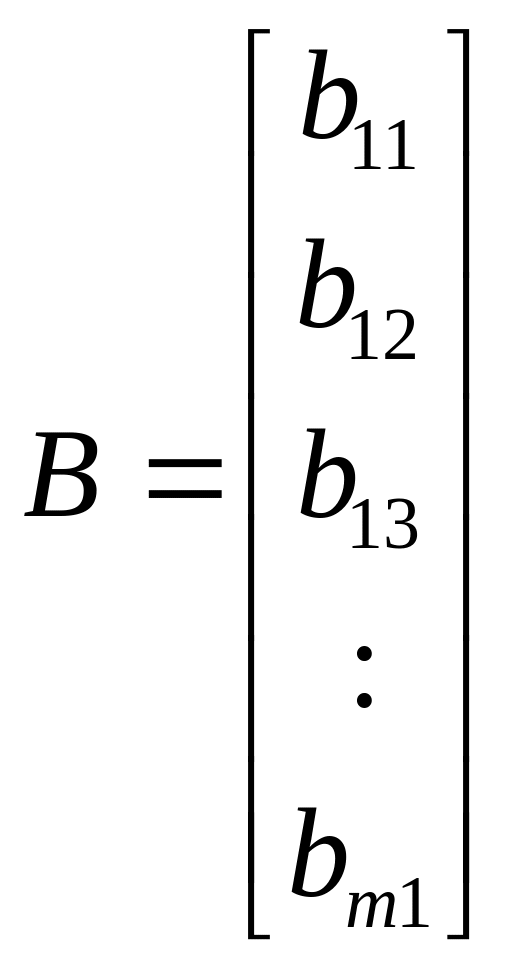Матрица, все элементы которой равны 0, называется нулевой и обозначается буквой 0.

Матрица, в которой число строк равно числу столбцов, называется квадратной.

Порядком квадратной матрицы называется число строк (или столбцов).

.

Порядок: 1, 2, n.

Элементы , , … квадратной матрицы образуют ее главную диагонали. Элементы , , … - побочную диагональ.

Квадратная матрица называется симметрической, если ее элементы, симметричны относительно главной диагонали, то есть :

Диагональной матрицей называется квадратная матрица, у которой все элементы, не лежащие на главной диагонали, равно 0, то есть:

.

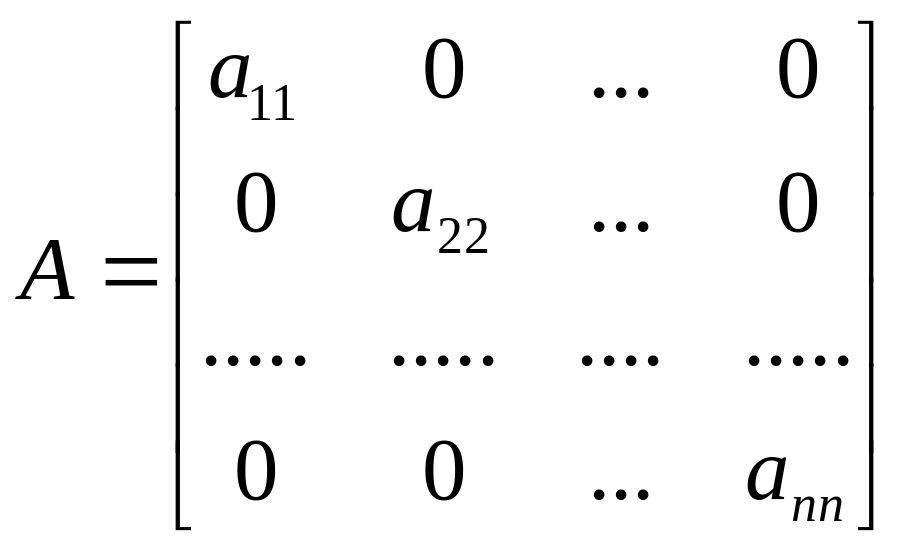Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1, и обозначается буквой E:

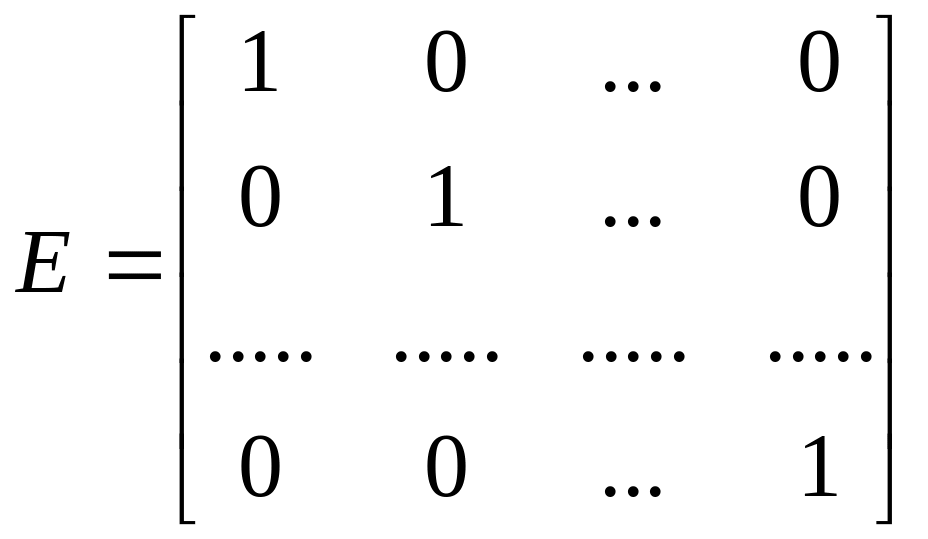
Треугольной матрицей называется матрица все элементы которой расположены по одну сторону от главной диагонали, равны 0. Различают верхнюю и нижнюю треугольные матрицы.

.

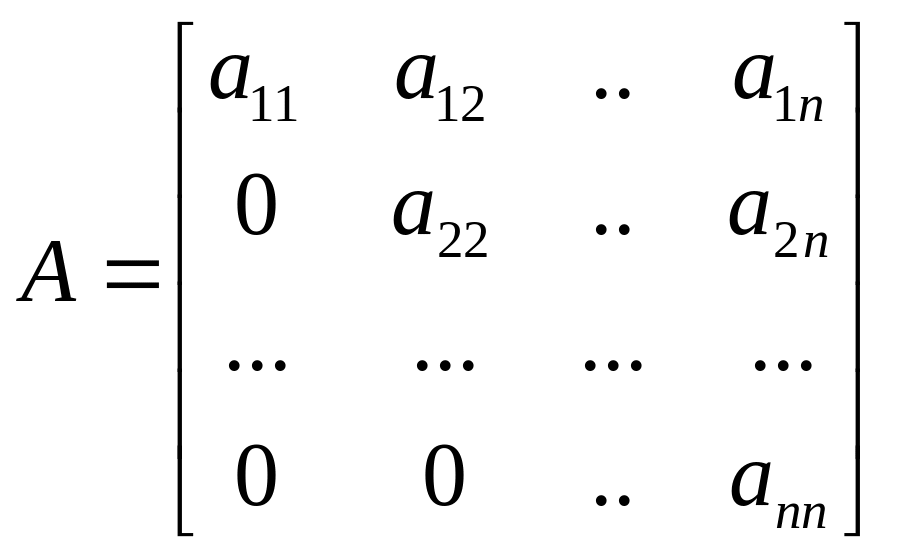2. Алгебра матриц.

Две матрицы одной размерности равны, если они состоят из одинаковых элементов.

.

Равенство, сложение и вычитание матриц определяются только для матриц одинаковых размеров.

Суммой двух матриц одной размерности называется матрица, элементы которой равны суммам соответствующих элементов матриц слагаемых.

.

, .

Пример:

, , = .

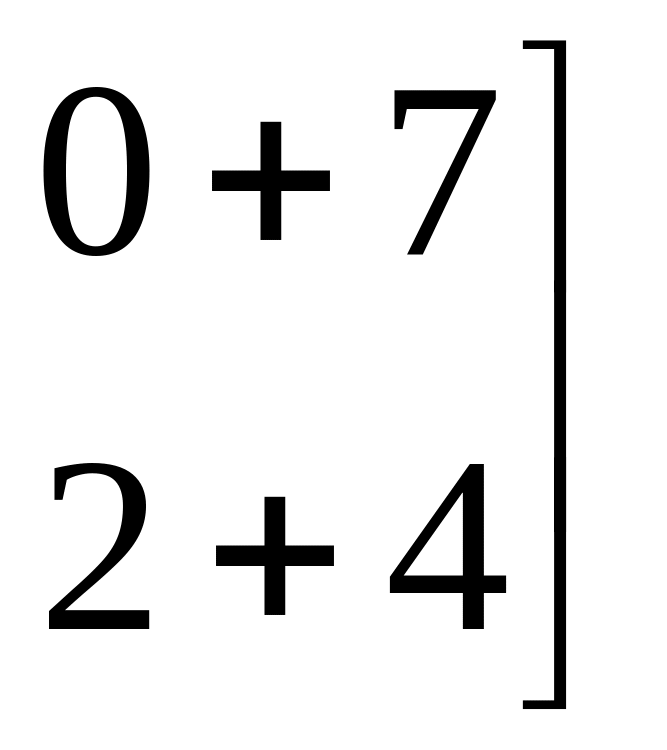Свойства сложения:

1⁰. - коммутативность.

2⁰. - ассоциативность.

3⁰.

Произведением матрицы на число называется матрица той же размерности, элементы которой равны произведению соответствующих элементов исходной матрицы на это число:

.

Матрицу называют матрицей противоположной матрице , обозначенной .

Замечание: Вычитание может быть выполнено таким образом:

.

Свойства операции умножения на число:

1⁰. .

2⁰. .

3⁰. .

Произведение матриц и существует только тогда, когда число столбцов равно числу строк .(то есть “ширина” матрицы , равна “высоте” матрицы ).

Матрица - произведение имеет столько строк, сколько их в , и столько столбцов, сколько их в матрице .

=

.

Элемент матрицы равен сумме произведений элементов - той строки матрицы на элементы -того столбца .

Пример:

.

.

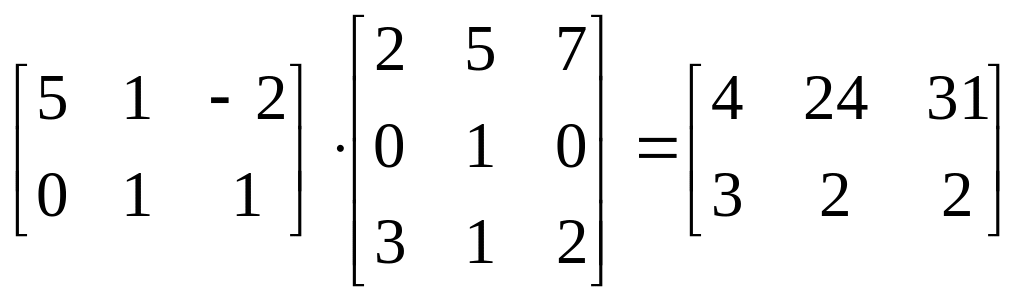Замечание: две квадратных матрицы одного и того же порядка всегда можно перемножить.

Свойства умножения:

1⁰. .

2⁰. .

3⁰. .

4⁰. В общем случае свойство коммутативности не выполняется: .

5⁰. .

6⁰. .

Матрица полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной относительно данной. Транспонированную матрицу обозначают .

.

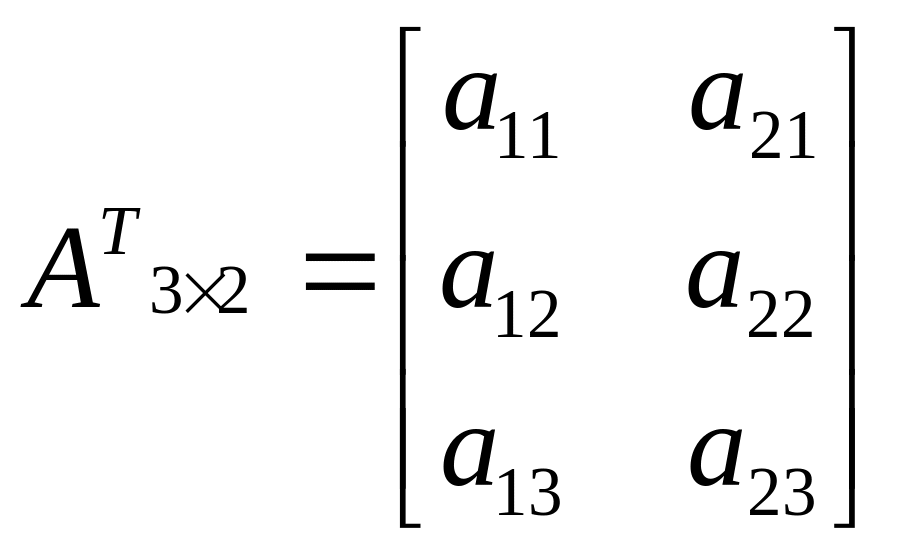Свойства транспонированной матрицы:

1⁰. .

2⁰. , где - число.

3⁰. .

4⁰. .