
- •1. Построение праволинейной грамматики.
- •2. Переход от праволинейной грамматики к автоматной.
- •3. Построение недетерминированного конечного автомата.
- •4. Сведение недетерминированного автомата к детерминированному.
- •5. Минимизация автомата.
- •6. Использование сетей Петри при переходе от грамматики к минимальному автомату.
- •7. Размещение состояний автомата.
- •8. Структурный и логический синтез распознающего автомата.
- •9. Реализация автомата
5. Минимизация автомата.
Построение минимального (но числу состояний) автомата, эквивалентного полученному в предыдущем разделе полностью определенному детеминированному конечному автомату, осуществляется в два этапа. На первом находится разбиение состояний автомата на классы эквивалентности, а на втором строится минимальный (иначе - приведенный) автомат. В начале составляется треугольная таблица (табл.6), клетки которой соответствуют всем парам (qi, qj), i≠j рабочих состояний. Она заполняется следующим образом. Если для рабочих состояний qi и qj в таблице существует входной символ хk, при котором переход из qi осуществляется в одно из рабочих состояний, а из qj - в состояние ошибки, то состояния qj и qj не эквивалентны, и соответствующая им клетка помечается крестом. Иначе, если какие-либо две строчки табл.5 содержат разное число рабочих состояний или отличаются позициями, занимаемыми рабочими состояниями, то обозначающие это строки состояния не эквивалентны. В противном случае в клетку таблицы 6 с координатами qi, qj запишем каждую пару состояний (qv, qw), в которые автомат может перейти из qi и qj при подаче одного и того же входного символа.
Таблица 6
1,3,7 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4 |
X |
X |
X |
|
|
|
|
|
|
|
|
||||||||||||||||||||
5 |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8 |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||||||||
9 |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
||||||||||||||||
10 |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||||||
11 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
||||||||||||||
12 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||||
13 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
||||||||||||
14 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|||||||||||
15 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
|
|
|
|
|
|
|
|
|||||||||
16 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
|
|
|
|
|
|
|
|
||||||||
17 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
|||||||
18 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
X |
|
|
|
|
|
|
|
|
|||||||
19 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|||||||
|
0 |
1,3,7 |
2 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
|
|
|
|||||||
В итоге невычеркнутые клетки табл. 6 соответствуют всем парам
эквивалентных состояний. Класс эквивалентности образуется состояниями,
которые попарно эквивалентны. В данном случае получается 4 класса
эквивалентности: {q5, q6}, {q8, q9,}, {q12, q15},{q13, q16, q18}. Каждое
состояние, не вошедшее ни в один класс эквивалентности, эквивалентно
лишь само себе и само образует этот класс. В нашем примере к
перечисленным классам необходимо добавить еще 9 классов
эквивалентности: q0, q1,3,7, q2, q4, q10, q11, q14, q17, q19,
Состояния минимального автомата обозначим буквами r с индексами:
r0={q5, q6}, r1={q8, q9}, r2={q12, q15}, r3={q13, q16, q18}, r4={q1,3,7},
r5={q2}, r6={q4}, r7={q10}, r8={q11}, r9={q14}, r10={q17}, r11={q19}, r12={q0}.
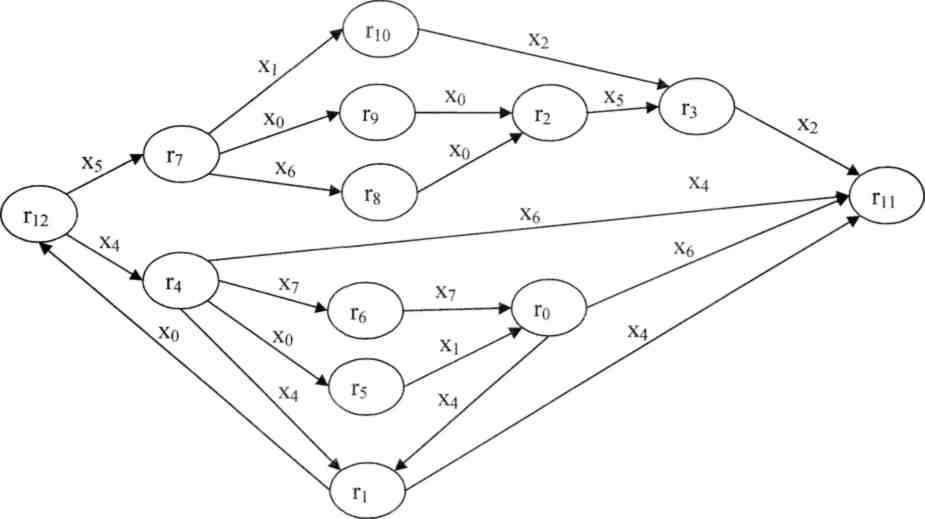
Минимальный автомат содержит, таким образом, 13 состояний, не считая состояния ОШИБКА. Граф переходов этого автомата приведен на рис. 3, а таблица переходов - в табл. 7
Рисунок 3
r |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
r0 |
|
|
|
|
r1 |
|
r11 |
|
r1 |
r12 |
|
|
|
r11 |
|
|
|
r2 |
|
|
|
|
|
r3 |
|
|
r3 |
|
|
r11 |
|
|
|
|
|
r4 |
r5 |
|
|
|
r1 |
|
r11 |
r6 |
r5 |
|
r0 |
|
|
|
|
|
|
r6 |
|
|
|
|
|
|
|
r0 |
r7 |
r9 |
r10 |
|
|
|
|
r8 |
|
r8 |
r2 |
|
|
|
|
|
|
|
r9 |
r2 |
|
|
|
|
|
|
|
r10 |
|
|
r3 |
|
|
|
|
|
r11 |
|
|
|
|
|
|
|
|
r12 |
|
|
|
|
r4 |
r7 |
|
|
