8 Понятие дифференциала

Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следовательно, в точке xсуществует конечная производная

Тогда по определению предела функции разность

                            (1)

является бесконечно малой величиной при  . Выразив из равенства (1) приращение функции, получим

                    (2)

(величина   не зависит от  , т. е. остаётся постоянной при  ).

Если  , то в правой части равенства (2) первое слагаемое  линейно относительно  . Поэтому при

оно является бесконечно малой того же порядка малости, что и  . Второе слагаемое  - бесконечно малая более высокого порядка малости, чем первое, так как их отношение   стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно  частью приращения функции; чем меньше  , тем большую долю приращения составляет эта часть. Поэтому при малых значениях  (и при  ) приращение функции можно приближенно заменить его главной частью  , т.е.

                (3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

или

Следовательно,

                   (4)

или

             (5)

Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (5) это видно из записи, в формуле (4) – нет.

Дифференциал функции можно записать в другой форме:

                      (6) или

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении xна величину  .

9 Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Внимание:  Производная произведения двух функций НЕ РАВНА произведению производных этих функций!

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

10 "Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.  Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование". 

11 Производная обратной функции

Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f ^-1, производная которой вычисляется по формуле

Теперь сформулируем правило нахождения производной обратной функции. Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах   и  соответственно. Если в точке   существует конечная отличная от нуля производная функцииf(x), то в точке   существует конечная

производная обратной функции g(y), причем  . В другой записи  . Можно это правило переформулировать для любого x из промежутка  , тогда получим  .

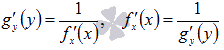12 Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти  . Этот предел существует  . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1^∞, 1⁰, ∞⁰ нужно прологарифмировать данную функцию и найти предел ее логарифма.

13    Теорема. Если х0 — точка экстремума функции f (x), то либо в этой точке производная обращается в нуль f ' (x0) = 0 (в стационарных точках), либо в этих точках производная не существует (в угловых точках).    Доказательство. Рассмотрим разложение функции в окрестности точки х0 в ряд Тейлора с остаточным членом в форме Пеано

Δ f (x) = f ' (x0)·Δ x + o(Δ x).

Так как остаточный член является бесконечно малой величиной относительно приращения аргумента, то

sign Δ f (x) = sign f ' (x0)·sign Δ x,

и знак приращения функции зависит от знака приращения аргумента sign (Δ x). Что недопустимо для точек экстремума. Следовательно производная функции в точке х0 или равна нулю, или не должна существовать.

14 Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х1, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х1. Если при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то при х =х1 функция имеет локальный максимум. Если же при переходе слева направо через эту точку х1 производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.    Комментарий. Если в достаточно малой окрестности точки х1 справедливо f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1, то в точке х1 функция имеет максимум; если f ' (x) < 0 при х < x1, f ' (x) > 0 при х > x1, то в точке х1 функция имеет минимум.    Доказательство. Пусть при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х1, имеем f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1. Применяя теорему Лагранжа к разности f (x) − f ( x1), получим

f ( x ) − f ( x1 ) = f ' ( c )·( x − x1 ).

где с лежит между точками х и х1. По условию теоремы

sign f ' ( c ) = − sign ( x − x1 ),

поэтому в произвольно малой окрестности точки х1 имеем

f ( x ) < f ( x1 ).

В этом случае точка х1 есть точка локального максимума, что и требовалось доказать.

15 Точка перегиба функции   внутренняя точка   области определения  , такая что   непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и   является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

16 Определение первообразной. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство   для любого х из заданного промежутка. Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство  . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину. Определение неопределенного интеграла. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается  . Выражение   называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x). Действие нахождения неизвестной функции по заданному ее дифференциалу называетсянеопределенным интегрированием, потому что результатом интегрирования является не одна функцияF(x), а множество ее первообразных F(x)+C.

свойства неопределенного интеграла (свойства первообразной).

Производная результата интегрирования равна подынтегральной функции.

Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

, где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

17  Интегрирование функций сводится к применению табличных интегралов. Но это не означает, что проинтегрировать можно только функции, указанные в таблице. Непосредственное интегрирование состоит в умении с помощью свойств алгебры и тригонометрии преобразовать подынтегральное выражение к табличным интегралам. Например, вычислим интеграл

.

Такого интеграла в таблице нет, но разложим полный квадрат числителя и почтенно разделим на знаменатель

.

Воспользуемся далее аддитивным свойством неопределённого интеграла по подынтегральной функции и окончательно найдём неопределённый интеграл

Пример. Найти интеграл 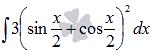 . Решение. Коэффициент 3 можно вынести из под знака интеграла на основании свойства: 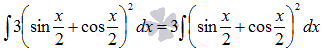  Преобразуем подынтегральную функцию (по формулам тригонометрии):   Так как интеграл суммы равен сумме интегралов, то   Пришло время обратиться к таблице первообразных: 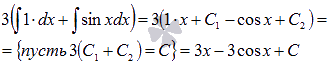  Ответ:  .

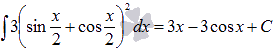18. Метод подведения под знак дифференциала основан на равенстве  . То есть, главной задачей является приведение подынтегральной функции к виду 

19. Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:      а)  , где   – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:  ;      б)  , где U – новая переменная. Формула замены переменной при такой подстановке:  .      Примеры.      1. Найти интеграл  .      Решение. Перепишем данный интеграл в виде  . Так как производная выражения   равна 2/х, а второй множитель 1/хотличается от этой производной только постоянным коэффициентом 2, то нужно применить подстановку  . Тогда  . Следовательно,        .      2. Найти интеграл  .      Решение.  , тогда   и        .

20. Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

Предполагается, что нахождение интеграла   проще, чем  . В противном случае применение метода неоправдано.

Получение формул

Для неопределённого интеграла

Функции   и   гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

Отсюда «следствие»:  , что очевидно неверно.

для определённого интеграла

В целом аналогично случаю неопределённого интеграла:

22. Для интегрирования рациональной функции  , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение: где   - правильная рациональная дробь.  Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q(x) в виде где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.  Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде: Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x).  Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.  Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: где   Затем применяются следующие формулы: Интеграл   может быть вычислен за k шагов с помощью формулы редукции

Пример 1

Вычислить интеграл  . Решение. Разложим подынтегральное выражение на простейшие дроби:        Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:        Следовательно,        Тогда        Теперь легко вычислить исходный интеграл

24 Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).